陶瓷、玻璃等硬脆材料的本构经典剖析【转发】
2017-07-10 by:CAE仿真在线 来源:互联网
对碳化硅、蓝宝石、石英玻璃、三氧化二铝等硬脆材料的性能进行切削仿真时,最关键的一个环节是选取该类材料的物理本构方程以及相关参数,以下为大家详细的分析选取方法。
硬脆材料常用的本构有三种,分别是:Johnson-Holmquist-Beissel model(JH1)、Johnson-Holmquist model(JH2)和Drucker-Prager model(DP)。其中,JH1本构是Johnson, G. R.和Holmquist, T. J.于1993年提出的。2005年,两位学者又通过Hugoniot(雨果尼奥)极限的方法将等效塑性应力(Mises)进行了归一化处理,并将JH1本构进行了改进,改进后的本构就是JH2本构。1952 年,D. C. Drucker和 W. Prager 为了研究静水压力对材料屈服强度的影响,将 Von-Mises 准则的表达式进行了修正,从而提出了DP本构(即D-P 准则),DP本构主要用于岩体和土壤等颗粒状材料的仿真分析。
查阅国内外文献可知,在陶瓷等硬脆材料切削(划痕)仿真领域最常用的是JH2本构,因此,以下对JH2本构的结构和构成情况进行详细说明。
JH2本构包括三个部分,分别是:强度模型、损伤模型和压力模型。
强度模型部分强度模型的表达式如式(1)所示:
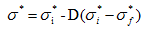
其中,
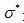
是等效应力,
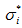
是损伤部分的等效应力,
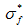
是损伤部分的等效应力,D是损伤变量,
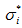
和
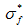
的表达式分别如式(2)和式(3)所示:
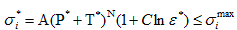
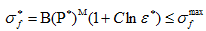
其中,A、B、C、M、N是材料参数,
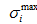
是未损伤部分的最大强度极限,
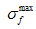
是损伤部分的最大强度极限。
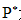
是归一化的压力,计算方法如式(4)所示:
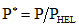
其中,P是单元的实际压力,
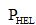
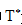
是归一化的最大静水拉(压)力,计算方法如式(5)所示:
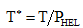
(5)
其中,T是材料所能承受的最大拉(压)力。C是应变率相关参数,
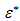
是无量纲的应变率(
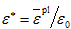
,
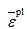
是等效塑性应变率,
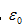
是参考应变率)。
初始损伤参数ω的表达式如式(6)所示:
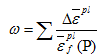
其中,
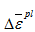
是等效塑性应变增量,
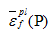
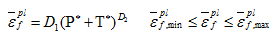
其中,D1、D2是材料参数,
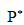
是归一化的压力,

是归一化的最大静水拉(压)力,
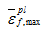
、
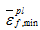
在没有相变的情况下,压力-密度关系方程如式(8)所示:
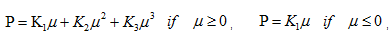
其中,
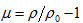
,其中
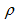
为材料的当前密度,
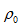
为材料的参考密度;
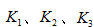
为材料参数,其中
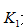
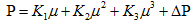
,其中
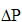
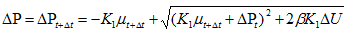
在此过程中,材料的部分弹性能量会转化为潜在的静水能量,式(9)中的β就是转化的百分比(0<β<1),∆U是转化的那部分能量。
以下是ABAQUS软件中碳化硅材料二维切削仿真的应力云图和切削力曲线
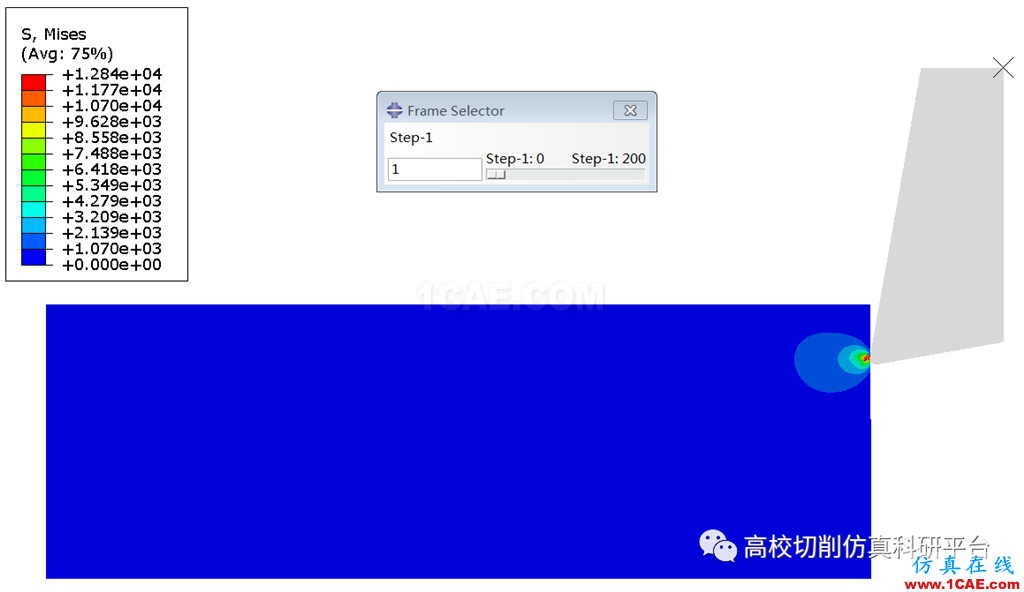
图1 碳化硅材料二维车削仿真中的Mises应力(第一帧动画云图)
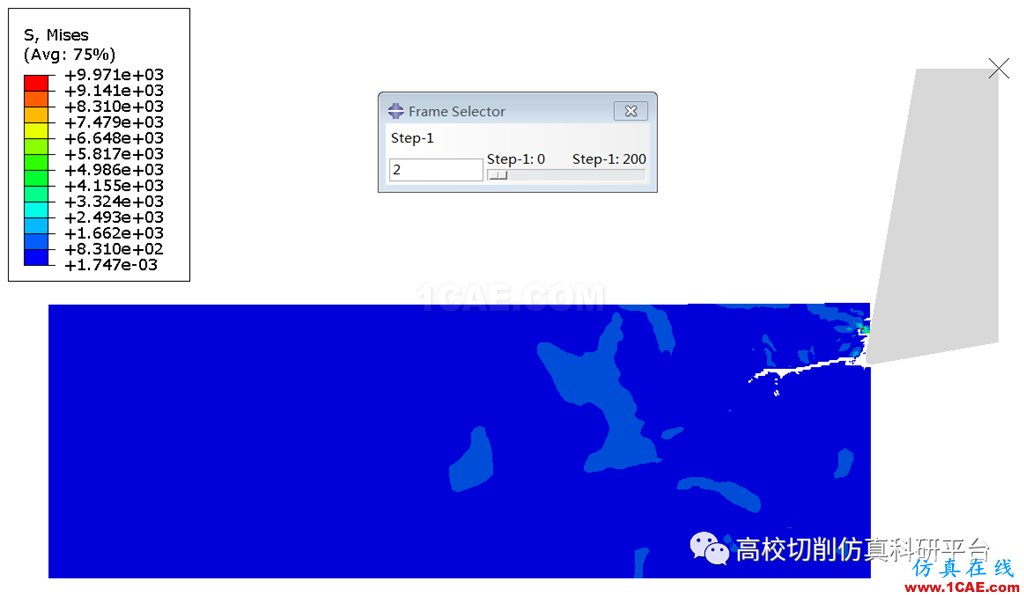
图2 碳化硅材料二维车削仿真中的Mises应力(第二帧动画云图)

图3 碳化硅材料二维车削仿真中的Mises应力(第五帧动画云图)
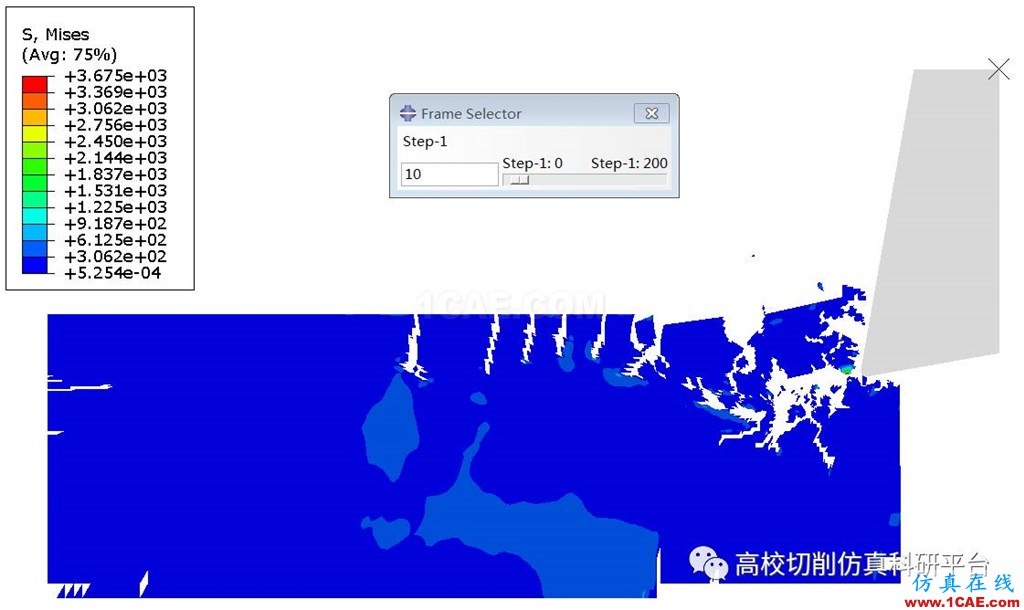
图4 碳化硅材料二维车削仿真中的Mises应力(第十帧动画云图)
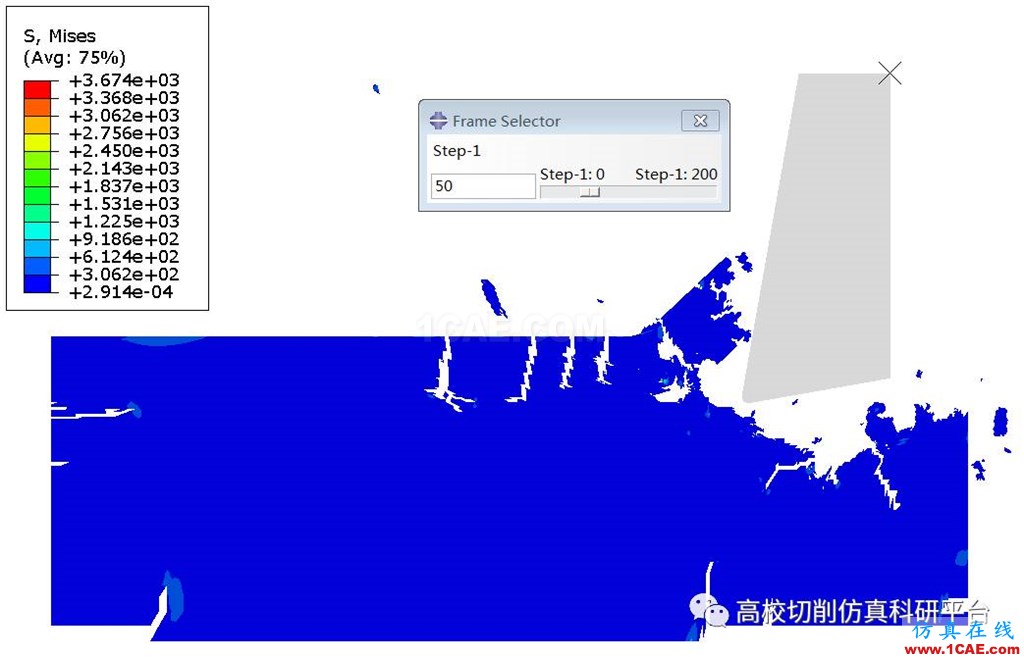
图5 碳化硅材料二维车削仿真中的Mises应力(第五十帧动画云图)
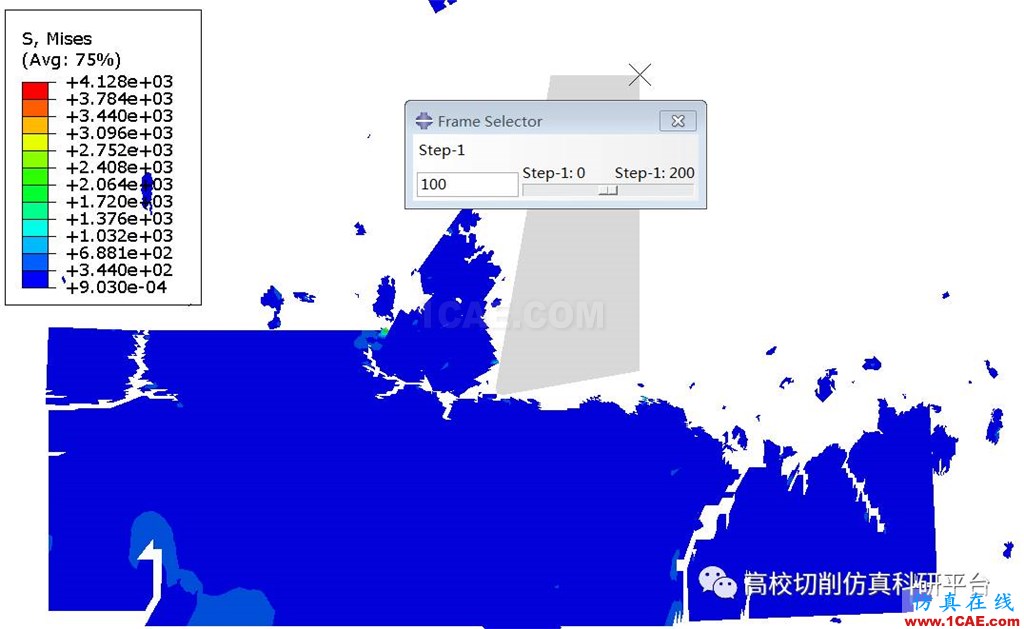
图6 碳化硅材料二维车削仿真中的Mises应力(第一百帧动画云图)
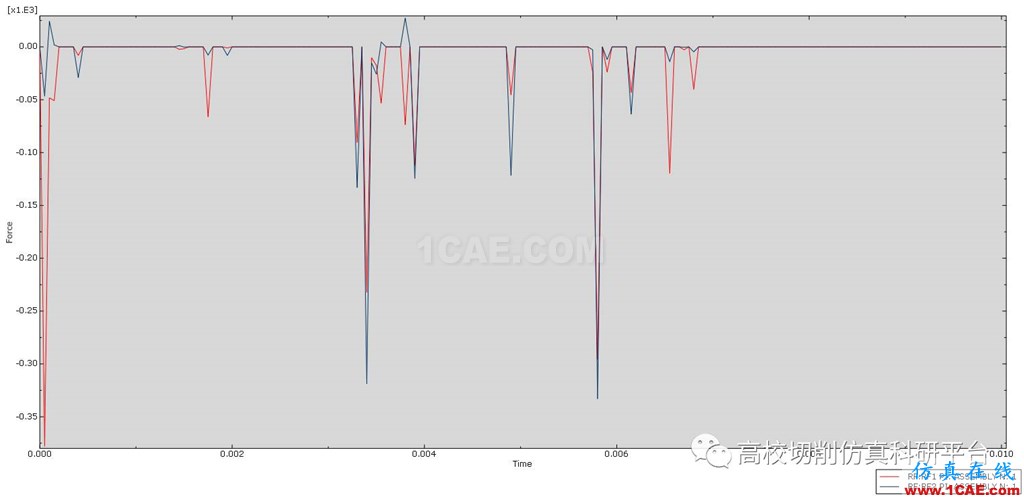
图7 碳化硅材料二维车削仿真中的切削力曲线
转自公众号: 高校切削仿真科研平台
相关标签搜索:陶瓷、玻璃等硬脆材料的本构经典剖析【转发】 Advantedge切削培训 Advantedge软件培训课程 Advantedge分析 加工仿真 车削 铣削 钻削 刨削和磨削仿真模拟 刀具磨损仿真 刀具涂层 冷却液仿真 Fluent、CFX流体分析






