史上最全ISIGHT优化算法（1）

2016-10-24 by:CAE仿真在线来源:互联网

ISIGHT软件是一款高度智能的软件机器人,为用户提供了高效、全面、强大、丰富、快捷、灵活、方便的优化集成平台,可以和市面上绝大多数工程软件、有限元分析软件、三维软件、办公软件、数值计算软件、数据库等进行集成,实现产品设计、仿真、优化的全流程,尤其是ISIGHT提供了非常全面的优化算法,下面我们就来一探究竟!

ISIGHT的优化算法分为四大类,分别为直接搜索法、梯度优化算法、全局优化算法、多目标优化算法,如下图所示。每种类都提供了大量的高效优化算法,各算法之间相互补充,各有所长,大大扩展了ISIGHT的优化能力。

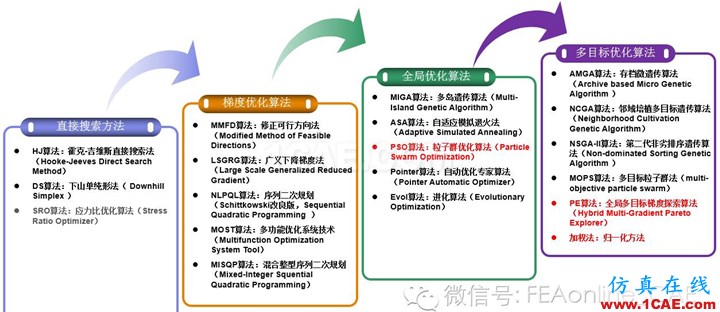
直接搜索方法

优势:

能有效探索初始设计点周围局部区域
探索阶段采用大步长,因此能够探索到比梯度优化算法更大的设计空间。
只需要评价设计点,而不需求梯度,广泛用于化学工程、流体力学等领域
能处理各种变量类型:实数型、整数型和离散型
特别适合设计变量数中等规模(即10~50个)和中度非线性的优化问题。
特定条件下,从数学上证明其收敛性。

缺点:

依赖初始设计点
有可能落入局部最小解
不适合计算时间较长的问题
不能利用工程经验和领域知识
无法并行计算

HJ算法:

开始于一个假定的初始点,搜索局部最小解。常用于一个还不能确定的可行的设计。使用混合的罚和目标值进行优化。这种技术的目标函数f(x)同时考虑了目标和约束罚。这种优化技术不要求目标函数f(x)可微,因为所用的算法不计算目标函数f(x)的导数,而是在当前点附近通过扰动设计变量探测合适的点,一次一个方向,直到找到一个更优的点,然后沿着这个方向继续搜索,直到没有更优的点。变量扰动的大小由相对步长确定,并且可以根据施加的步长减小因子逐步减小,直到获得收敛的解。

DS算法:

对空间进行采样,通过子区域,向相反的方向移动单纯形面上最差点,获得更好的结果。下山单纯形法是一个几何直观的算法。一个单纯形是一个由n+1个向量组成的n为空间几何体。指定每个局部向量的方向就完全定义了单纯形。在二维空间,单纯形是一个三角形,在三维空间,是一个四面体。单纯形通过多步朝着最小的位置,这些步可以分割为反射,这些反射包含移动单纯形的顶点,在这些顶点目标函数是最大的(也就是最差的),单纯形相反的面就是更小的(更好)点。反射表现在单纯形的体积上,当需要的时候扩展单纯形,增加单纯形的尺寸,从而加速收敛。相反的,缩小单纯形,以便能够适应最小或通过小的开口,例如沙漏的颈部。当使用一个较大的初始步时,这种方法具有寻找全局最小值的最大可能性。此时,初始单纯形在设计空间中占据了更大的分数,掉入局部最小值的机会就降低了。然而,对于复杂的多维设计空间,这种方法也会出现问题。

SRO算法:

应力比优化算法是一个完全的应力设计方法,通常用于结构优化。需要一套设计变量,典型的有厚度、面积、转动惯量,而且需要相应的许用应力的约束,设计变量的变化规律关系为x_new= x_old(sigma_actual/sigma_allowable)^power。用户定义的相关设计变量和约束,进行名称转换xAt... ---> stressAt,每个设计变量可具有任意多个约束与其相关。当编辑设计变量的时候,算法会自动选择施加关键的约束。

梯度优化算法

优势:

能有效探索初始设计点周围局部区域
如果设计空间是连续、单峰的形态,能够沿最快下降方向快速探索
特定条件下,能从数学上证明其收敛性。

缺点:

非常依赖初始设计点,有可能落入局部解
当变量数增加时,求解梯度的计算代价急剧增加
如果无法求得解析的梯度公式,则必需采用有限差分算法求解梯度

MMFD算法:

利用沿着初始设计点局部的面域,直接考虑不等式和等式约束,进而快速获得局部优化设计。当从一个可行的设计点开始时,应用非常好。通常需要多次迭代来计算(使用每个变量的梯度)搜索方向,并且是一个一维搜索。沿着激活的约束一直搜索,直到没有更好的结果出现。

LSGRG算法:

利用沿着初始设计点局部的面域;依照激活的约束提高设计;直接考虑不等式和等式约束;LSGRG使用广义下降梯度算法求解约束非线性优化问题。该算法使用的搜索方向要保证任何激活的约束对于一些在该方向小的移动仍然是激活的。广义下降梯度法是早期的下降梯度法的扩展,早期的下降梯度法只能求解等式约束问题。

NLPQL算法:

利用沿着初始设计点局部的面域;快速找到局部优化设计点;直接考虑不等式和等式约束;NLPQL是一种特殊的序列二次规划算法(SQP)。通过二阶近似拉格朗日函数,线性化约束,得到一个二次规划子问题,并进行求解。依赖于计算节点数,目标函数和约束函数沿着搜索方向预定义的测试的同时进行评估。执行线性的并行搜索,这是拉格朗日的优势功能。

MOST算法:

利用沿着初始设计点局部的面域;整型变量采用修正的分歧定限法;直接考虑不等式和等式约束;MOST可有效的应用于连续优化问题和整型或离散设计空间的优化问题,一个或多个设计变量都可以限制为整型。优化时,所有的离散变量被圆整为整型,范围从1到允许的值都可以。MOST先执行一个SQP优化,以获得问题的连续解。在这个阶段所有的整型变量作为最小步长为1的连续变量处理。如果存在任何整型(或离散)变量,MOST使用连续解作为修正的分歧定限法的起始点,在此阶段,整型变量一次下降一个。简化的连续优化问题对每个下降的变量进行求解,将他们的值固定在整数水平,大于或小于先前发现的优化值。然后再将所有剩余的整型变量作为最小步长为1的连续变量处理。这种技术假设存在潜在的连续设计空间,并且能够实现。这种技术不适用于纯粹的组合优化。

MISQP算法:

利用沿着初始设计点局部的面域;整型变量采用修正的分歧定限法;快速找到一个局部的优化设计点;直接考虑不等式和等式约束;本方法在每个迭代步对拉格朗日目标函数进行二阶近似,对输出约束进行线性近似,通过拉格朗日目标函数的海森(Hessian)矩阵开始,使用BFGS(Broydon-Fletcher-Goldfarb-Shanno)方法逐步更新矩阵。在每个迭代步采用二次规划问题进行求解,以获得更好的解,直到找到最终收敛的优化解。

由于篇幅原因,我们稍后会对另外两种类型的算法进行介绍,敬请期待!

开放分享：优质有限元技术文章,助你自学成才