Isight梯度优化算法浅析

2016-10-24 by:CAE仿真在线来源:互联网

梯度算法通过在设计空间中的当前位置设定一个前进方法和搜索步长从而获得设计空间中的另一个位置,并判断收敛性。Isight中梯度优化算法有三种NLPQL,LSGRG和MMFD,这里通过寻找数学函数表达式的最小值问题,来展示这三种算法搜寻最优解的效率。

优化问题:

min f(x)=100*(x2-x1^2)^2+10*(x1-1)^2

s.t. x1^2+x2^2=<9.0

isight优化步骤:

1、构建优化流程,application组件采用calculator,process 组件选用optimization;

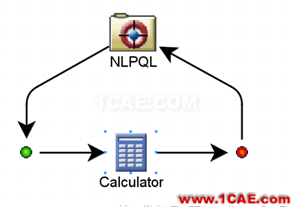
图1-优化流程构建

2、设置优化算法、设计变量、约束及目标,设计变量初始值为x1=2.0,x2=3.0;

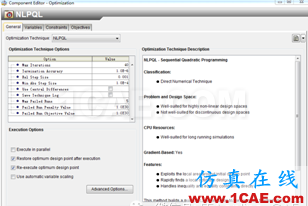
图2-优化算法及参数设置

3、查看优化结果,并比较3种梯度算法搜寻全局最优解的效率。

图3-三种优化算法的迭代历史

图 3给出了三种算法的搜寻历程,算法收敛准则均设置为1.0e-6,设计空间为以(0,0)为圆心半径为3.0的圆域内,初始点为(2.0,3.0)不在设计空间内部,NLPQL算法迭代27次能搜寻到全局最优解(0.986,0.975),LSGRG算法迭代10次找到局部最优解 (1.590,2.544),这个局部解刚好在设计区域的边界上,因为LSGRG算法的搜寻梯度和它的临界约束相关,MMFD算法迭代8次找到局部解 (1.523,2.342),这个点刚好满足目标函数高阶项接近零。以上结果可以发现,初始点不在设计区域内,NLPQL算法通过多次迭代能搜寻到全局最优解,而LSGRG和MMFD算法能用较少的迭代次数搜寻到一个局部最优解而完成迭代过程。

下面考察3种算法在无约束情况下搜寻最优解的效率,去掉设计区域在圆域内的限制,设计空间改为无限平面域,初始点位置不变,从图4中可以看出NLPQL和LSGRG算法都能搜寻到全局最优解,而MMFD算法依然在一个局部最优解处停止搜寻,从迭代历程上看NLPQL算法和LSGRG算法相比能以更少的迭代次数获得全局最优解。

本文以数学函数表达式为例对比了isight中3中梯度算法的效率,在有约束情况下 NLPQL能搜寻到全局最优解,而LSGRG和MMFD 算法只能搜寻到局部解;在无约束情况下,NLPQL比LSGRG算法能更快速搜寻到全局最优解

开放分享：优质有限元技术文章,助你自学成才