matlab中FFT的使用

2017-02-14 by:CAE仿真在线来源:互联网

一.调用方法
X=FFT(x);
X=FFT(x,N);%当x的长度小于N,则会在x末端补零,使长度等于N
x=IFFT(X);
x=IFFT(X,N)

用MATLAB进行谱分析时注意:
(1)函数FFT返回值的数据结构具有对称性。
例:
N=8;
n=0:N-1;
xn=[4 3 2 6 7 8 9 0];
Xk=fft(xn)

输出:

Xk =

39.0000 -10.7782 + 6.2929i 0 - 5.0000i 4.7782 - 7.7071i 5.0000 4.7782 + 7.7071i 0 + 5.0000i -10.7782 - 6.2929i

Xk与xn的维数相同,共有8个元素。Xk的第一个数对应于直流分量,即频率值为0,值为xn各元素的和。
(2)做FFT分析时,幅值大小与FFT选择的点数有关,但不影响分析结果。在IFFT时已经做了处理。要得到真实的振幅值的大小,只要将得到的变换后结果乘以2除以N即可。
二.FFT应用举例

例1:x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t)。采样频率fs=100Hz,分别绘制N=128、1024点幅频图。

clf;
fs=100;N=128; %采样频率和数据点数
n=0:N-1;t=n/fs; %时间序列
x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信号
y=fft(x,N); %对信号进行快速Fourier变换
mag=abs(y); %求得Fourier变换后的振幅
f=n*fs/N; %频率序列
subplot(2,2,1),plot(f,mag); %绘出随频率变化的振幅
xlabel('频率/Hz');
ylabel('振幅');title('N=128');grid on;
subplot(2,2,2),plot(f(1:N/2),mag(1:N/2)); %绘出Nyquist频率之前随频率变化的振幅
xlabel('频率/Hz');
ylabel('振幅');title('N=128');grid on;
%对信号采样数据为1024点的处理
fs=100;N=1024;n=0:N-1;t=n/fs;
x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信号
y=fft(x,N); %对信号进行快速Fourier变换
mag=abs(y); %求取Fourier变换的振幅
f=n*fs/N;
subplot(2,2,3),plot(f,mag); %绘出随频率变化的振幅
xlabel('频率/Hz');
ylabel('振幅');title('N=1024');grid on;
subplot(2,2,4)
plot(f(1:N/2),mag(1:N/2)); %绘出Nyquist频率之前随频率变化的振幅
xlabel('频率/Hz');
ylabel('振幅');title('N=1024');grid on;

运行结果:
matlab中FFT的使用

fs=100Hz,Nyquist频率为fs/2=50Hz。整个频谱图是以Nyquist频率为对称轴的。并且可以明显识别出信号中含有两种频率成分:15Hz和40Hz。由此可以知道FFT变换数据的对称性。因此用FFT对信号做谱分析,只需考察0~Nyquist频率范围内的福频特性。若没有给出采样频率和采样间隔,则分析通常对归一化频率0~1进行。另外,振幅的大小与所用采样点数有关,采用128点和1024点的相同频率的振幅是有不同的表现值,但在同一幅图中,40Hz与15Hz振动幅值之比均为4:1,与真实振幅0.5:2是一致的。为了与真实振幅对应,需要将变换后结果乘以2除以N。

例2:x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t),fs=100Hz,绘制:
(1)数据个数N=32,FFT所用的采样点数NFFT=32;
(2)N=32,NFFT=128;
(3)N=136,NFFT=128;
(4)N=136,NFFT=512。

clf;fs=100; %采样频率
Ndata=32; %数据长度
N=32; �T的数据长度
n=0:Ndata-1;t=n/fs; %数据对应的时间序列
x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %时间域信号
y=fft(x,N); %信号的Fourier变换
mag=abs(y); %求取振幅
f=(0:N-1)*fs/N; %真实频率
subplot(2,2,1),plot(f(1:N/2),mag(1:N/2)*2/N); %绘出Nyquist频率之前的振幅
xlabel('频率/Hz');ylabel('振幅');
title('Ndata=32 Nfft=32');grid on;

Ndata=32; %数据个数
N=128; �T采用的数据长度
n=0:Ndata-1;t=n/fs; %时间序列
x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t);
y=fft(x,N);
mag=abs(y);
f=(0:N-1)*fs/N; %真实频率
subplot(2,2,2),plot(f(1:N/2),mag(1:N/2)*2/N); %绘出Nyquist频率之前的振幅
xlabel('频率/Hz');ylabel('振幅');
title('Ndata=32 Nfft=128');grid on;

Ndata=136; %数据个数
N=128; �T采用的数据个数
n=0:Ndata-1;t=n/fs; %时间序列
x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t);
y=fft(x,N);
mag=abs(y);
f=(0:N-1)*fs/N; %真实频率
subplot(2,2,3),plot(f(1:N/2),mag(1:N/2)*2/N); %绘出Nyquist频率之前的振幅
xlabel('频率/Hz');ylabel('振幅');
title('Ndata=136 Nfft=128');grid on;

Ndata=136; %数据个数
N=512; �T所用的数据个数
n=0:Ndata-1;t=n/fs; %时间序列
x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t);
y=fft(x,N);
mag=abs(y);
f=(0:N-1)*fs/N; %真实频率
subplot(2,2,4),plot(f(1:N/2),mag(1:N/2)*2/N); %绘出Nyquist频率之前的振幅
xlabel('频率/Hz');ylabel('振幅');
title('Ndata=136 Nfft=512');grid on;
matlab中FFT的使用

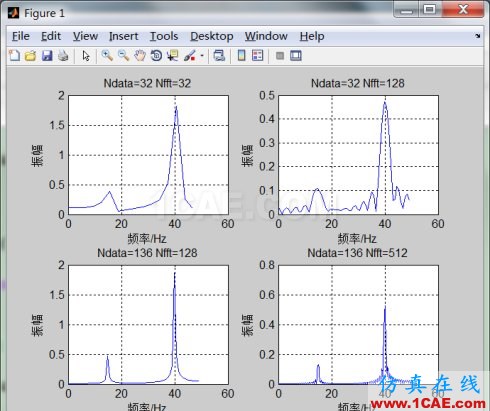
结论:
(1)当数据个数和FFT采用的数据个数均为32时,频率分辨率较低,但没有由于添零而导致的其他频率成分。
(2)由于在时间域内信号加零,致使振幅谱中出现很多其他成分,这是加零造成的。其振幅由于加了多个零而明显减小。
(3)FFT程序将数据截断,这时分辨率较高。
(4)也是在数据的末尾补零,但由于含有信号的数据个数足够多,FFT振幅谱也基本不受影响。
对信号进行频谱分析时,数据样本应有足够的长度,一般FFT程序中所用数据点数与原含有信号数据点数相同,这样的频谱图具有较高的质量,可减小因补零或截断而产生的影响。