Matlab有限元计算
2017-08-25 by:CAE仿真在线 来源:互联网
对于开始学习有限元的人来说,简单了解下有限元计算的基本思路是很有必要的,因此这篇文章仅仅以一个简单的一维线性弹簧单元为例,简述一下有限元计算的基本思想,主要参考书目《有限元方法基础教程》-Daryl L. Logan和《matlab有限元分析与应用》-P.I. Kattan。前者有详细的刚度矩阵等推导,主要从理论上对有限元方法进行说明,后者主要是结合著名的矩阵实验室matlab对结构有限元进行分析与计算,两者可以结合来看。
下面我就《有限元方法基础教程》一书中的习题2.17为例,使用matlab来说明一下如何对其进行计算。
习题2.17
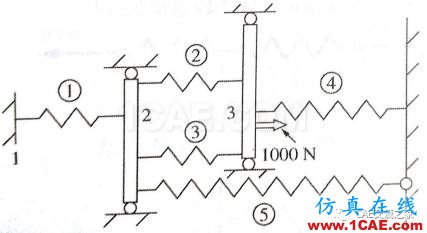
如图所示的五个弹簧组装,确定节点2和节点3的位移、节点1和节点4的反力。假设节点2和节点3处连接弹簧的刚性垂直杆一直保持水平,但是自由滑动、向左或者向右移动。在节点向右施加外力1000N。令k1=500N/mm,k2=k3=300N/mm,k4=k5=400N/mm。
众所周知,有限元计算的基本流程主要包含六个部分:
①离散化域
②写出单元刚度矩阵
③集成整体刚度矩阵
④引入边界条件
⑤解方程
⑥后处理
①离散化域
有限元模型的建立有两种方法,一种是直接建立,另一种是网格划分,对于像杆单元,弹簧单元质量单元等直接建立有限元模型比较方便,但是像梁单元,实体单元等人为建立就很复杂,一般就是先建立好几何模型再进行网格划分,以此得到有限元模型。
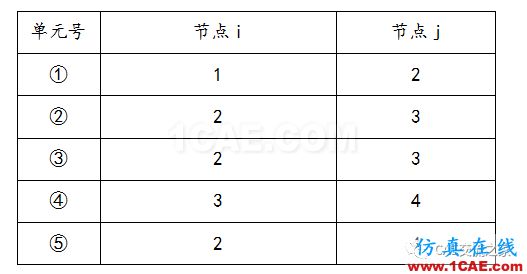
对于此题,使用直接建立法即可。由图中可以看出可以离散成五个弹簧单元,各弹簧单元以及对应节点如下:
②写出单元刚度矩阵
对于静力结构分析来说,最大的难点就在单元刚度矩阵的得出。简单的单元刚度矩阵像本题中的弹簧单元使用直接平衡法就能得到,复杂的可能就要用到能量法或者加权残余法等。
本例中直接给出弹簧单元的刚度矩阵形式,这样,根据该矩阵形式,我们可以构造一个函数SpringElementStiffness专门用于得到弹簧单元的刚度矩阵,下面是《matlab有限元分析与应用》配套给出的弹簧单元刚度矩阵生成函数(以下函数均为书中给出):

这样,通过调用该函数能够方便的生成上述5个单元的刚度矩阵:

③集成整体刚度矩阵(直接刚度法)
得到单元刚度矩阵之后,可以直接利用叠加法得到整体刚度矩阵。由于每个节点的力是由分担该节点的单元节点相加而成,因此能够直接通过将各单元对应节点叠加,得到总体刚度矩阵,这个也叫直接刚度法,对应的matlab程序如下:

将单元矩阵k的对应元素叠加到总体刚度矩阵对应的节点位置,由于这里总共有五个单元,因此需要调用该函数五次得到总体刚度矩阵:

④引入边界条件
对于上图中,边界条件属于混合型,既有位移型也有力型,具体有:
u1=0 u4=0 f2=0 f3=1000N
其中
u3 u4 f1 f4是未知的,需要我们求出。引入上述边界条件得到以下总体方程:

⑤解方程
上述方程组可以直接提取第三行和第二行先进行求解得到u2和u3的值,即求下面方程:

直接使用矩阵反除求出u2与u3的值,再将位移值带入总体位移矩阵,得到力值。由于后面会多次使用力值计算程序,因此将该程序也编写为m文件进行调用,如下:

然后计算得到总位移与总力矩阵

⑥后处理
所有求解完毕之后,可以返回来从新得到各个单元内力,具体计算程序如下:
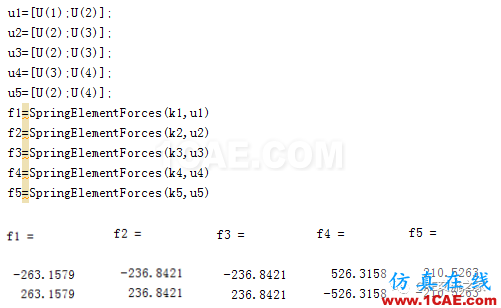
通过上述求解结果可以得到各节点的位移以及单元受力情况。当然这只是对于最简单的一维线性弹簧单元,如果要扩展到二维,三维,单元更换为杆,梁,面等,单元刚度矩阵显然会更加复杂,对于具体的边界可能还要对刚度矩阵进行修正,但是整体的求解思路类似。
相关标签搜索:Matlab有限元计算 MatLab培训 MatLab培训课程 MatLab在线视频教程 MatLab技术学习教程 MatLab软件教程 MatLab资料下载 MatLab代做 MatLab基础知识 Fluent、CFX流体分析 HFSS电磁分析 Ansys培训 Abaqus培训






