连载-“老朱陪您学Civil”之梁桥抗震4
2016-10-29 by:CAE仿真在线 来源:互联网
连载-“老朱陪您学Civil”之梁桥抗震,你们的最爱-朱老师,小迈致力于与您分享一手技术资料,用技术创造幸福,你我一起!

3.Civil程序计算振型的三种方法
在一般的有限元分析中,由于系统的自由度很多,同时在研究系统的响应时,往往只需要了解少数较低的特征值及相应的特征向量,因此在有限元分析中,发展了一些适应上述特点而效率较高的解法(子空间迭代法、lanczos)。
midas Civil中除了提供精确的特征向量法分析外,还提供了与荷载相关的Ritz向量分析法。多重Ritz向量能用于线性和非线性结构的动力分析。与精确特征向量法相比,多重Ritz向量法用更少的时间可产生更精确的结果。
3.1子空间迭代法(wilson著作《结构静力与动力分析》)
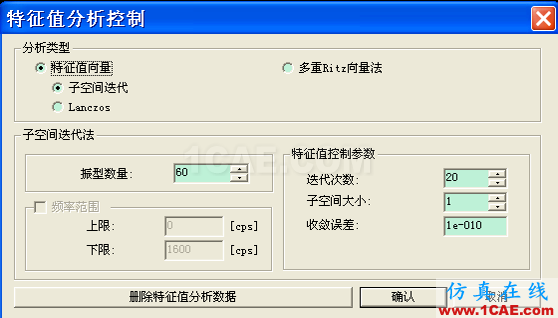
子空间迭代法是求解大型矩阵特征值问题的最常用最有效的方法之一,它适合于求解部分特征值解,被广泛应用于结构动力学的有限元分析中。
子空间迭代法是假设r个起始向量(采用移频法,通过特征值的移动和已收敛的特征向量的移出,使r保持在较小的数值,从而显著提高计算效率和改进收敛速度)同时进行迭代(通过求解减缩广义特征值问题)以求得矩阵的前p(<r)个特征值和特征向量。(如果r不是足够大,一方面可能漏掉可能激起的振型;另一方面又可能引入不可能激起的振型)。
3.2 Lanczos方法
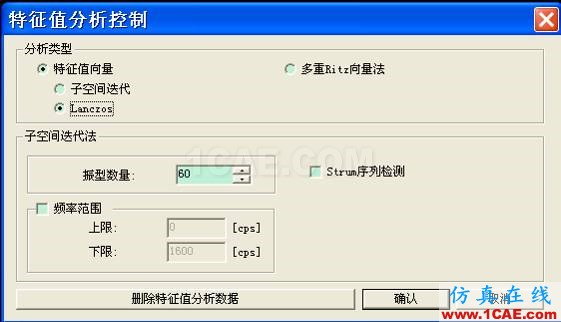
Lanczos方法和Ritz向量法的共同特点是直接生成一组Lanczos向量或者Ritz向量,对运动方程进行缩减,然后求解缩减了的运动方程的特征值问题,避免了迭代步骤(采用直接叠加法),从而具有更高的计算效率。
Lanczos法和Ritz向量法本质上一致,但是在实际计算中,由于计算机的截断误差和舍入误差,导致数值上的不稳定性(例如虚假的多重特征值现象),因此妨碍了Lanczos方法的实际应用。20世纪70年代以后,很多研究工作者提出了不少Lanczos向量的重正交技术以调高其算法的稳定性,Ritz向量法从这个意义上说可以是这种,但由于他改变了成Lanczos向量的算法公式,导致以后求解的不是对角矩阵的特征值问题,而是一般矩阵特征值问题。
3.3多重Ritz向量法(求解的是一般矩阵特征值问题)
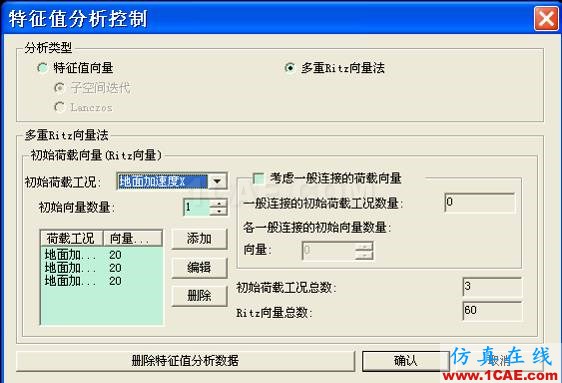
多重Ritz向量法认可结构动态响应是空间荷载分布的函数,考虑动力荷载的空间分布(当定义了初始向量后,第一个向量块的静态响应就来源于该初始荷载向量),可以避免漏掉可能激起的振型和引入不可能激起的振型,能够显著提高计算效率。
3.4 子空间迭代法、Lanczos法和多重Ritz向量法算例比较(荷载作用是对称)
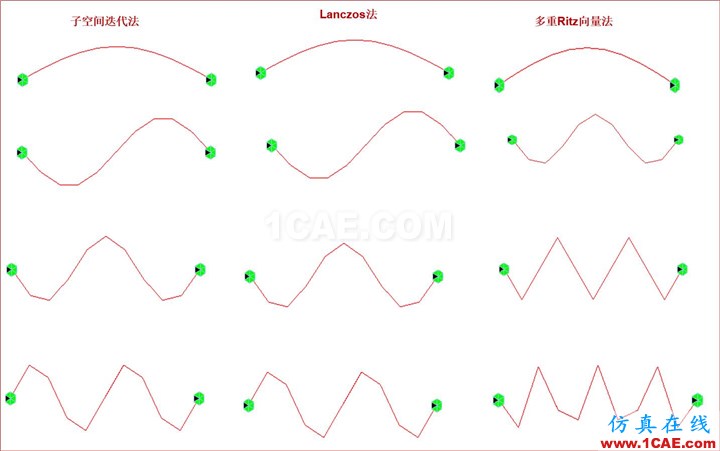
由图可以清楚的发现:多重Ritz向量法和另外2种分析方法得到的振型图是大不相同的。通过模态查看,可以发现多重Ritz向量法所有振型都是对称的(荷载作用是对称的),因为它考虑了空间荷载分布状态及动力贡献,所以他忽略了所有反对称振型 。对于反对称振型,并不是由荷载激发的,荷载在这些振型的动力贡献为零。故:反应谱分析时较好的方法是采用多重Ritz向量法。
4.已知振型(模态)情况下如何计算反应谱下的结构受力情况
4.1单振型施加惯性力的方法

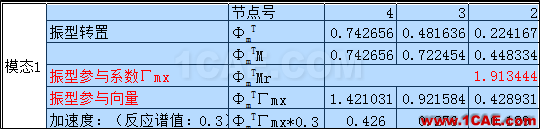
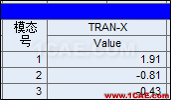
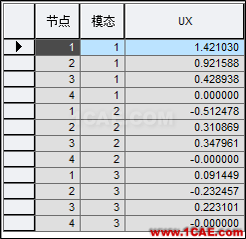
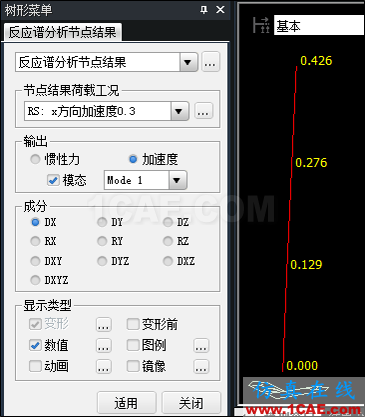
4.2各振型的组合结果

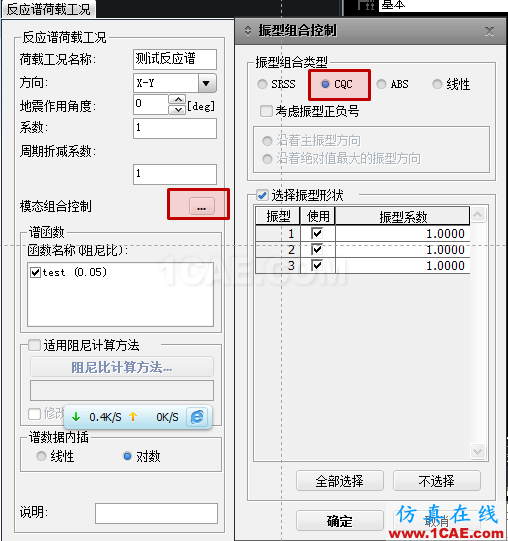
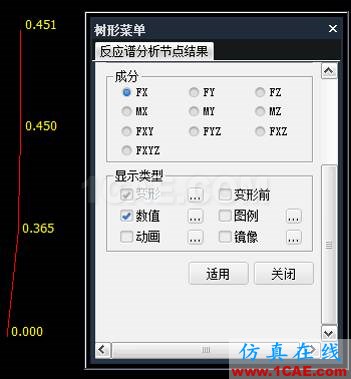
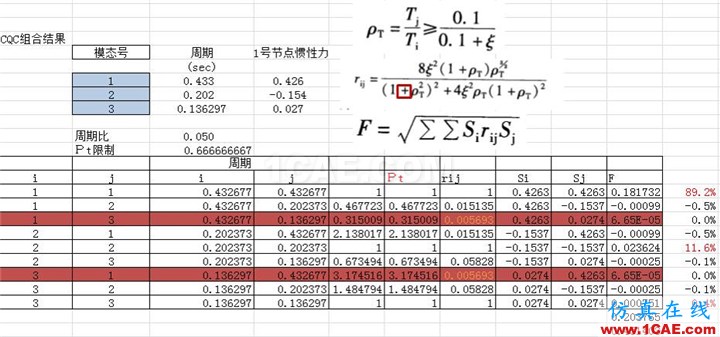


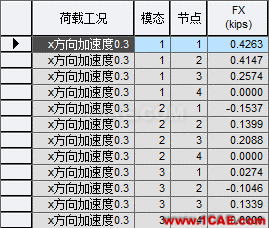
*连载-每周更新,敬请期待,也可留言向朱老师提问
相关标签搜索:连载-“老朱陪您学Civil”之梁桥抗震4 Midas Civil分析 Midas Civil培训 Midas Civil培训课程 Midas Civil在线视频教程 Midas Civil技术学习教程 Midas Civil软件教程 Midas Civil资料下载 Midas Civil代做 Midas Civil基础知识 Fluent、CFX流体分析 HFSS电磁分析 Ansys培训






