竖向剪刀撑及平联对高耸型螺旋钢管支架 稳定性影响分析
2016-10-29 by:CAE仿真在线 来源:互联网
中铁十七局三公司 总工程师 周永明
摘 要 论文分析了高耸型螺旋钢管支架剪刀撑设置方法,通过理论公式与迈达斯软件计算对比,验证了软件计算支架结构稳定性的准确性。利用软件计算四种剪刀撑设置方案下支架整体结构的稳定性,以及增加平联后支架结构稳定性,计算结果表明剪刀撑竖向均匀布置、适当刚度的设置原则对提高支架结构稳定性最为有效。
1 概述
桥梁施工中,尤其是钢管混凝土拱肋安装支架、斜拉桥主塔上横梁现浇支架,通常设计为高耸型螺旋钢管落地支架结构,支架高度均在30 m以上,主要通过结构布置方案、设置竖向剪刀撑及平联来保证支架结构的稳定性。目前,关于支架剪刀撑施工与计算的资料较少,导致高耸型支架施工中出现不设支撑、剪刀撑设置不合理、材料浪费等现象,增大了支架结构失稳的风险。
日常施工中计算支架的稳定性经常采用公式[1]
N/φA≤f (1)
式中:N为单根钢管轴力,为根据构件长细比选取的稳定系数,A为钢管横截面面积,f为材料容许应力。
此计算方式存在一定的局限性,忽略了剪刀撑及平联对整体结构稳定性的影响;支架剪刀撑及平联设置仅通过施工经验布置,不能有效地反映整体支架结构的稳定性。
本文主要从3个方面分析:①利用Midas计算单根螺旋钢管失稳临界荷载,再通过理论计算公式验证软件计算的准确性;②不同的剪刀撑设置方案对整体高耸型支架结构稳定性的影响;③支撑设置中平联对支架稳定性的影响。
2 稳定性分析及计算原理
为保证施工中临时结构正常工作,必须满足强度、刚度、稳定性的要求。高耸型支架结构即使强度等性能满足要求,仍然会出现失稳破坏,故稳定性分析是非常重要的内容。失稳一般可分为局部失稳和整体失稳[2]。
局部失稳是指在钢结构中,由于板件宽厚比过大,在受压、受弯、受剪或应力复杂的情况下发生屈曲的现象。整体失稳是指结构在未达到强度极限,甚至未达到屈服极限时,由于侧向屈曲引发承载能力丧失,从而导致结构破坏的现象。当结构所受荷载达到某一数值时,若施加一微小的增量,即稍有扰动,则结构的平衡位置将发生很大的改变,这种情况叫做结构的失稳或屈曲,相应的荷载称为屈曲荷载或临界荷载[2]。临界荷载计算式为[3]
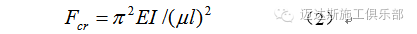
式中:Fcr为结构整体失稳临界荷载值;E为材料弹性模量;I为截面惯性矩;μ为构件长度系数;l为构件长度。
本文主要计算结构的整体稳定性,迈达斯屈曲分析用于预测一个理想弹性结构的理论屈曲强度,模型假设为完善体系,符合欧拉公式假设条件[4]。
Midas计算临界荷载Fcr为

式中:α为结构第1模态临界荷载特征值;变量为构件所受外界压力,即支架上部荷载传递到螺旋钢管的压力;常量为构件自重。
临界荷载特征值可以反映支架结构整体稳定性,特征值越大、支架稳定性越强,反之则弱[5]。
3 剪刀撑及平联对支架结构稳定性的影响
3.1 计算模型
根据支架结构形式,首先建立单根钢管模型,计算屈曲临界荷载特征值,再通过理论计算公式验证软件计算结果的准确性,根据单根立管的稳定性计算原理,分别计算4种不同剪刀撑布置方案下的稳定性,并通过修改模型中剪刀撑的型号得出材料强度对支架稳定性的影响规律,在此基础上计算增加平联后支架整体结构的稳定性。
在施工中,高耸螺旋管支架最经济实用的型号为φ630×9mm。以某项目斜拉桥主塔横梁现浇支架剪刀撑布置方案为例(见图1),验证软件计算的准确性。主塔横梁支架结构采用“碗扣件+单层贝雷梁+钢管支墩”形式,支架结构钢管支墩高度40m,共采用4根钢管立柱,主梁截面以上竖向设置4组剪刀撑,单组剪刀撑竖向尺寸为4m,采用[20b型号槽钢,主塔横梁恒载、活载根据计算分配至单根钢管立柱轴力为1 250 kN。
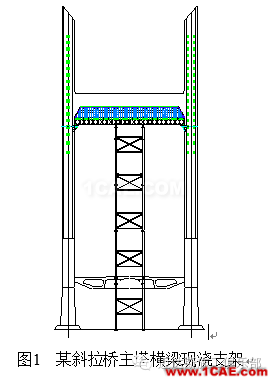
3.2 单根螺旋钢管稳定性分析
1)软件计算结果
建立单根螺旋钢管模型,屈曲模态数量设为10,以第1模态屈曲特征值为临界荷载特征值。建立自重荷载工况及轴力荷载工况,其中螺旋钢管自重设置为常量,轴力设置为变量。
计算第1模态临界荷载特征值α=0.215124,故Fcr=267 kN。
2)理论公式计算结果
钢管高度40 m,根据长细比计算判定为大柔度压杆,失稳破坏先于强度破坏。φ630×9mm螺旋钢管临界荷载特征值
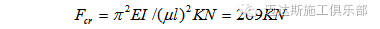
对比计算结果可知,二者计算屈曲误差仅为0.37%。
3.3 设置剪刀撑对支架稳定性的影响
支架高度40m,纵桥向、横桥向间距均为3.2m。剪刀撑采用[20b,每组剪刀撑竖向高度均为4 m。
方案1:距离支架顶部2.5 m设置第一道横撑,支撑竖向间距相同均为10 m,沿支架竖向均匀布置至底部。
方案2:距离支架顶部0.4 m设置第一道横撑,支撑竖向最大间距为13 m,剪刀撑间距沿支架竖向逐渐增大,布置不均匀。
方案3:距离支架顶部0.4 m设置第一道横撑,减少一组剪刀撑设置,沿支架竖向设置3组剪刀撑,剪刀撑最大间距17.5 m,均匀布置。
方案4:距离支架顶部8.5 m设置第一道横撑,沿支架竖向设置3组剪刀撑,剪刀撑最大间距9.5 m,均匀布置。4种支架结构布置方案见图2。
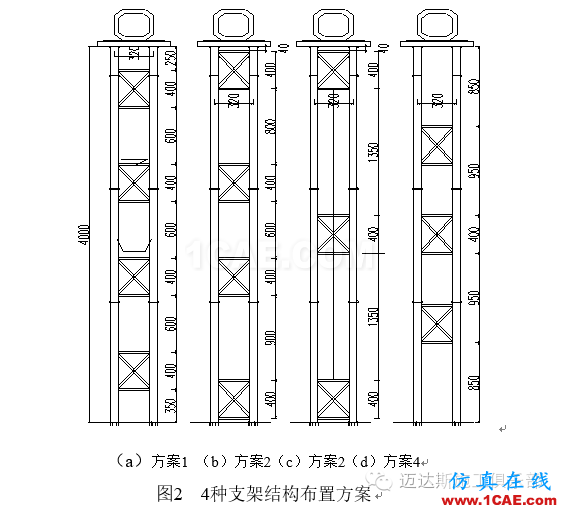
利用Midas计算4种剪刀撑布置方案下结构临界荷载特征值,以临界荷载特征值>4为控制条件,选择最优方案。通过临界荷载特征值即可得到支架结构的屈服临界荷载,临界荷载特征值越大,结构稳定性越强。4种支架结构计算模型见图3。
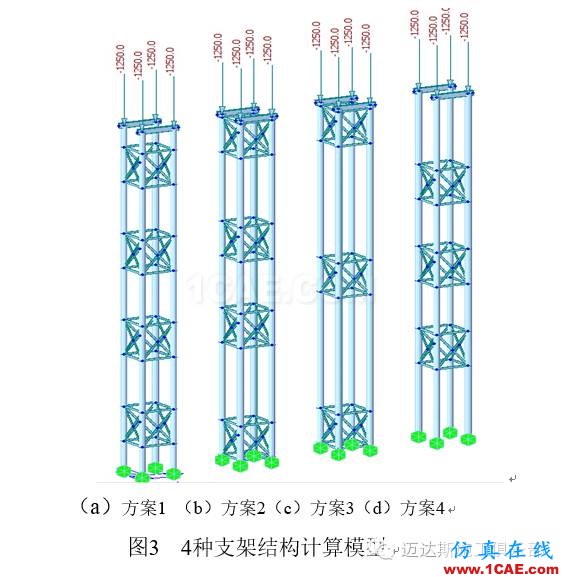
通过对4种剪刀撑布置方案的稳定性进行分析,得到屈曲临界荷载特征值,见表1。其中,方案1屈曲荷载特征值为最大4.26,满足结构稳定性的要求,其他3种布置方法对结构稳定性均有不同程度地降低。通过比选剪刀撑材料[20b、[16b可知,[20b剪刀撑满足经济、安全的要求。因此按照支架竖向均匀布置四组剪刀撑方案对结构稳定性的提高最为显著。
表1 屈曲临界荷载特征值
|
方案 |
剪刀撑 布置情况 |
特征值系数 [20b剪刀撑 |
特征值系数 [16b剪刀撑 |
|
1 |
4组剪刀撑均匀布置 |
4.261713 |
3.194621 |
|
2 |
4组剪刀撑不均匀布置 |
4.176274 |
3.074904 |
|
3 |
3组剪刀撑大间距布置 |
4.007574 |
3.076377 |
|
4 |
3组剪刀撑小间距布置 |
3.096551 |
3.011036 |
3.4增加平联对支架结构的影响
高耸型螺旋管支架立柱拼接常采用焊接、栓接结合的连接方法,安装过程中必须严格控制立柱的垂直度。剪刀撑的设置是否需要安装平联,平联对支架结构安装过程中及结构完全受力后的稳定性是否有所提高,通过对上述4种剪刀撑布置方案增加平联(图4)进行结构稳定性屈曲荷载特征值计算,验证平联对结构稳定性的影响。
增加平联后屈曲临界荷载特征值见表2。由表2可知,增加平联后屈曲临界荷载特征值减小,说明支架结构的稳定性没有提高反而降低,可见支架剪刀撑的刚度过大对支架结构整体稳定性存在不利的影响。因此应根据不同的支架结构形式,合理选择剪刀撑材料及布置方案。在保证支架稳定性的前提下,剪刀撑应具有较小的变形范围,分散剪刀撑的应力集中,避免剪刀撑整体刚度过大对整体结构的稳定性降低的现象。
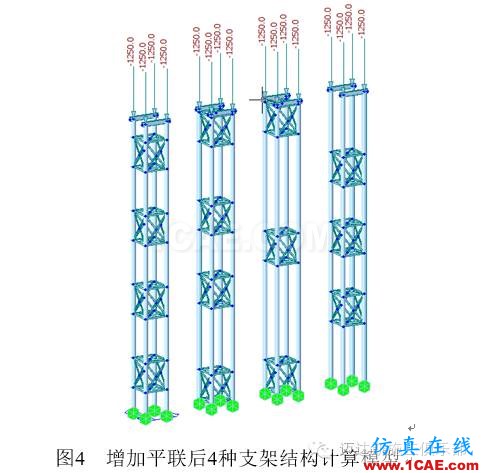
表2 增加平联后屈曲临界荷载特征值
|
方案 |
剪刀撑 布置情况 |
特征值系数 [20剪刀撑 |
特征值系数 [16剪刀撑 |
|
1 |
4组剪刀撑均匀布置 |
3.984193 |
2.971397 |
|
2 |
4组剪刀撑不均匀布置 |
3.969254 |
2.930360 |
|
3 |
3组剪刀撑大间距布置 |
3.972236 |
2.932418 |
|
4 |
3组剪刀撑小间距布置 |
3.112366 |
2.972812 |
4 应用实例
北京至沈阳铁路客运专线玉龙特大桥203#~204#墩以120 m系杆拱跨越既有玉龙路,拱肋安装支架高度25 m,拱肋钢管支架模型见图5。根据剪刀撑对支架整体结构稳定性的计算,临时支架采用Φ180×10mm钢管,剪刀撑采用∠75×8组成2m×2m的格构柱形式,支架高度随安装位置高度确定。支架纵桥向采用φ133钢管构成桁架进行连接,横桥向采用I32b工字钢贯通连接,侧面用工字钢与预埋锚头连接牢固,支架安装时可采用钢丝绳临时固定,防止倾倒,待支架构成整体后再拆除钢丝绳。
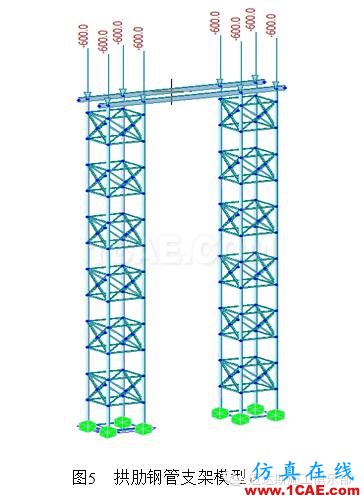
根据拱肋节段重量计算荷载,单根立柱荷载为600 kN,建立拼装支架整体模型见图5,计算结构第1模态临界荷载特征值为4.559078>4,满足现场施工稳定性的要求,支架强度及刚度通过计算满足规范要求。
支架设计采用Φ180×10无缝钢管,取代常用Φ630×9mm钢管。剪刀撑材料选用刚度较小的角钢,降低了拼装支架的整体用钢量。现场施工剪刀撑沿支架竖向均匀设置,刚度适中,取得了良好的效果。
5 结论
1)通过理论公式与软件计算高耸型支架结构稳定性,验证了软件计算支架结构稳定性的可行。临时结构设计时可以采用软件计算整体结构稳定性,避免了采用单根螺旋管稳定系数计算整体结构稳定性的局限性。
2)根据不同剪刀撑布置方案的计算与比选,可以得出均匀等间距布置方式对提高整体支架稳定性最为显著;剪刀撑应该根据支架的高度、螺旋管立柱型号、立柱布置间距等因素选择合适的材料,单纯的提高剪刀撑的强度与刚度并不能提高整体结构的稳定性。
3)应根据安装需求设置平联,计算结果表明在剪刀撑满足支架结构稳定性的情况下,增加平联反而会降低整体结构的稳定性,施工中不宜选取此类剪刀撑刚度过大的设置方案。
参考文献
[1] 满洪高,李君君,赵方刚.桥梁施工临时结构工程技术[M].北京:人民交通出版社,2012.
[2] 姚谏,夏志斌,.钢结构-原理与设计[M].2版.北京:中国建筑工业出版社,2011.
[3] 张志国,张庆芳.钢结构[M].北京:中国铁道出版社,2008.
[4] 葛俊颖.桥梁工程软件midas Civil 使用指南[M].北京:人民交通出版社,2013.
[5] 宗周红,任伟新.桥梁有限元模型修正和模型确认[M].北京:人民交通出版社,2012.
相关标签搜索:竖向剪刀撑及平联对高耸型螺旋钢管支架 稳定性影响分析 Midas Civil分析 Midas Civil培训 Midas Civil培训课程 Midas Civil在线视频教程 Midas Civil技术学习教程 Midas Civil软件教程 Midas Civil资料下载 Midas Civil代做 Midas Civil基础知识 Fluent、CFX流体分析 HFSS电磁分析 Ansys培训






