【转载】弧长法(Riks method)通用求解程序（Code by myself）

2016-11-16 by:CAE仿真在线来源:互联网

算例1. 如图1所示的平面杆系结构,顶点受到竖直向下的力P作用,用本程序(Riks method)进行计算,并将计算结果与精确解进行比较,如图2所示,通过对比可以说明本程序是正确的。

弧长法(Riks method)通用求解程序(Code by myself) - Yusd - 玉石殿

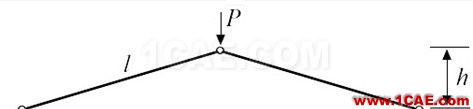
图1 计算简图

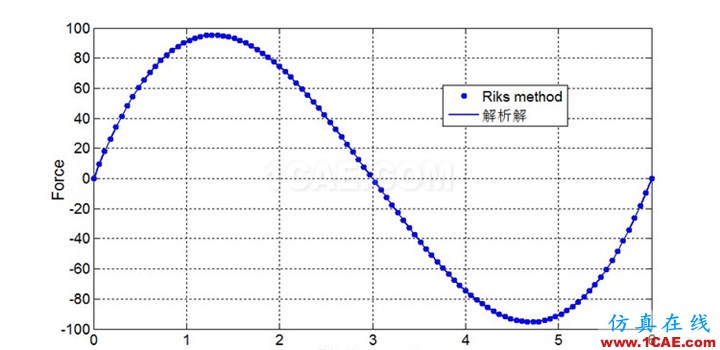
图2 跨中节点荷载—位移曲线对比

算例2:图3是经典的Lee's frame简图,一个在端部正交的铰接约束平面刚架,在距离正交点一定距离处有集中力F作用。之所以称其为经典算例是因为它的荷载位移曲线同时集中了跳跃(snap-through )和回弹(snap-back)现象,传统的求解策略根本无法对其进行荷载—位移路径跟踪,在此,弧长法展现了很大优势,图4是运用本程序得到刚架的变形动画,图5是加载点的荷载位移曲线,并将其与ABAQUS计算结果进行对比,通过对比表明该程序的是正确的。

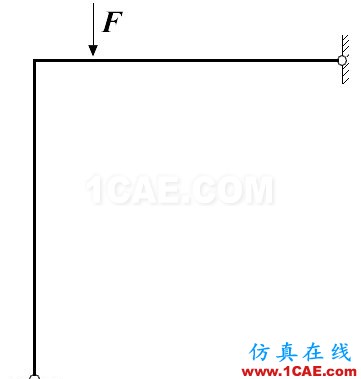
图3 Lee's Frame 简图

图4 Lee's frame变形动画

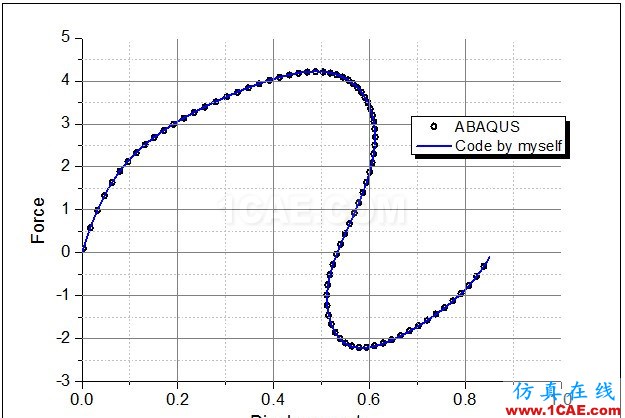
图2 加载节点荷载—位移曲线对比

程序核心部分:

读取数据文件(节点、单元、约束、截面属性、参考力、控制弧长、最大控制参量)
while 控制参量(如位移、最大荷载因子) < 最大控制参量
计算当前切线刚度矩阵 K_Global
计算参考位移 X_Ref= 参考力\K_Global
计算初始荷载因子 lamda0=Arclength/sqrt(1+X_Ref'*X_Ref);
判定初始荷载因子方向 +/- lamda0
更新节点坐标,更新外力
计算当前节点反力
计算节点不平衡力Val
while norm(Val)>1e-6
计算不平衡力产生的位移X_Val
计算荷载因子修正参数delta=X_Val'*X_Ref/(1+X_Ref'*X_Ref);
修正荷载因子lamda1=lamda0-delta;
更新初始荷载因子lamda0=lamda1;
更新节点坐标,更新外力
计算当前节点反力
计算节点不平衡力Val