[转载]Midas进行Pushover分析的总结

Midas进行Pushover分析的总结 1.1版

一. 不得不说的基本概念

1. Pushover是什么和前提条件

Pushover也叫推倒分析,是一种静力弹塑性分析方法,或者叫非线性静力分析方法,在特定前提下,可以近似分析结构在地震作用下的性能变化情况。

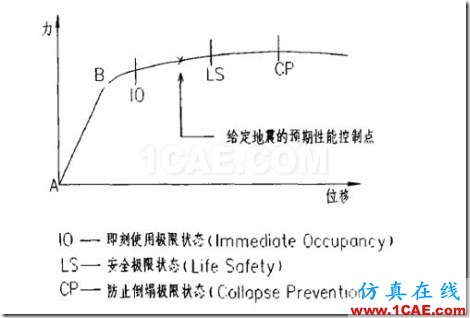
给桥梁用某种方式,比如墩顶集中力方式,施加单调增加的荷载,相应的荷载位移关系就会呈现明显的非线性特征。这里可以认为IO是处在正常使用状态,LS为承载能力极限状态,CP是完全倒塌破坏。从IO开始结构开始进入弹塑性状态,在LS前结构的损伤尚可修复,且结构整体是安全的,而越过LS损伤就难以修复了,但是CP前还不至于倒塌。设计中对于不同构件或部位,在特定地震作用下,其性能要求是不一样的。

而特定的前提很明确,就是在整个地震反应时程中,结构反应由单一振型控制,在《公路桥梁抗震细则》(以下简称《细则》)中,认为常规桥梁中的规则桥梁都满足这一条件(条文说明6.3.4),因此E1地震可以采用简化反应谱方法,也可用一般的多振型反应谱方法,E2则用Pushover。

2. Pushover的分析目的

在E2地震作用下,《细则》要求:

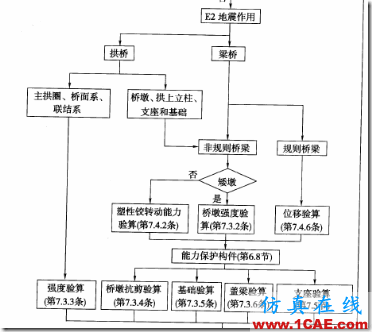
可见,对于规则桥梁,只需要检算墩顶位移就可以了。对于单柱墩,容许位移可按7.4.7条推荐的公式进行计算,而双柱墩按7.4.8条要求进行Pushover分析根据塑性铰的最大容许转角(7.4.3)得到。而无论是7.4.3还是7.4.7都要用到Φy和Φu,对于圆形或者矩形截面可按附录B计算,而特殊的截面,可按7.4.4和7.4.5的要求计算。计算方法可以自己编程实现,也可用现成的软件如Response2000等来作为工具。

而对于在特定的E2地震作用下,墩顶的位移,都需要用Pushover的能力谱法得到。所以Pushover的目的一个是画出荷载位移曲线后,找到塑性铰达到最大容许转角时的曲线点,计算出墩顶容许位移,第2个目的是应用能力谱法,找到性能点,得到E2地震作用下,墩顶的位移。后者要求小于前者。同时,对于延性构件来说,还要判断性能点对应的各塑性铰状态,最好能让塑性铰都处于IO和LS或者LS和CP之间,从而既可满足一定延性达到可修或者不倒的目的。

对于非规则桥梁,可以用线性或非线性时程分析的方法,直接得到E2地震作用下极限弯矩和各塑性铰的状态并验算强度或者转角。

二. Midas的Pushover分析的基本步骤

1. 建立结构的弹性材料和截面特性,建立结构的基本有限元模型,施加相应荷载;

2. 定义结构的质量,进行特征值分析,得到结构的自振频率和振型;

3.进行钢筋混凝土构件设计,输入截面配筋情况,定义设计标准,强度折减系数,钢筋混凝土材料特性等,然后运行截面设计过程。如果定义塑性铰时不使用自动计算功能的话,那么就可以跳过这一步;

4.定义塑性铰时一般需要使用自动计算功能!但是要使用自己的MΦ曲线计算工具,得到有效刚度等。注意,按规范要求用来计算塑性铰最大转角的Φy是要求第2段折线为水平,而这种方法一般不适合Midas进行Pushover时塑性铰的定义,所以要另外求双折线模型或者三折线模型的屈服弯矩等参数。

5. 分配塑性铰给单元

6. 进行Push-Over分析,绘出其荷载位移曲线;

7. Midas自带的能力谱法比较适合建筑,是否可用于桥梁还需要专门研究,如果使用Midas自带的能力谱法则下面8-12就可以省略了;

8. 使用“强度折减系数”法,这就要求使用自己开发的工具,根据结构的自振特性,把荷载位移曲线转换为能力曲线;

9. 建立特定地震作用下的反应谱,转换为相应的需求谱,并与能力曲线绘在一起;

10. 需求谱与能力曲线的交点即为性能点。把能力曲线双折线化,得到其屈服位移,根据性能点和屈服位移得到位移延性比;

11. 根据位移延性比,计算强度折减系数,并绘出新的需求谱;

12. 使用自己开发的工具对10,11进行迭代最后得到最终的位移延性比,并计算出相应的位移,即计算墩顶位移。

13. 计算塑性铰的最大容许转角,找到某塑性铰首次到达最大容许转角时的步骤序号,得到最大容许位移;

14. 进行验算!

三. Midas进行Pushover的几个关键问题

1.桩基础的模拟

桩基础的刚度对计算结果的影响很大,可以使用专门的桩基础计算软件如B90,Pile等先计算出其刚度矩阵,经过适当处理后,使用Midas的一般弹性支承来模拟。

2.P-M曲线的由来和作用

对于纯弯构件或者偏压钢筋混凝土构件,对应某个轴力P,显然就能根据规范求出一个Mu极限弯矩来。这个规范就是JTJ85规范,奇怪的是Midas到现在也没在钢筋混凝土构件设计中加入JTG04规范,大概是因为后者已经在RC设计中考虑了,不过现在的问题是Pushover是否认可新的RC设计呢?现在还不得而知。

不过都是极限状态法,原理上也没区别,所以我们规范取JTJ85而混凝土和钢筋材料还是可以取JTG04的,但是材料的1.25系数现在一定要去掉而取为1,在这种情况下,Midas会按JTG04的混凝土设计强度和钢筋的标准强度取值计算,显然如果是正式的”钢筋混凝土构件设计”验算的话,钢筋的材料应该取1.2才对,不过我们是在为Pushover准备数据,而Pushover在从”钢筋混凝土构件设计”里取数据的时候,会自动按材料分项系数为1计算。

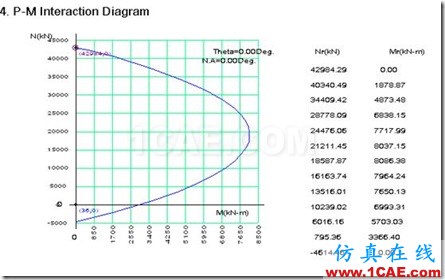
经过“钢筋混凝土构件设计”中的柱截面验算后,就可以得到一个P-M图,图的意义就是前面说的P-Mu的关系,这个可以用手算一个矩形截面直接核对。在Pushover计算过程中,塑性铰的P可能是不断变化的,于是塑性铰的MΦ曲线也会变化,我们在定义塑性铰时如果自动计算,则Midas会自动在当前P得到Mu后,再根据某个规则计算得到My,再根据My得到全部MΦ曲线。而如果用户定义那么包括P-M关系本身等所有数据都要全部自定义,会是一件极其麻烦的事情。

3.自动计算的MΦ曲线是什么

Midas塑性铰定义,在选择自动计算时,其屈服弯矩的计算其实根本就不使用应力应变关系,而是用的规范里的极限状态法计算的极限弯矩转换而来。根据规范和截面尺寸,钢筋分布的定义,求出任何轴力作用下的Mu并不困难,问题是知道Mu后怎么得到My呢?我们可以深入分析一下Midas的塑性铰定义方法。

钢筋混凝土构件一般可选择双线和三折线两种,我们只考虑双线这种情况。

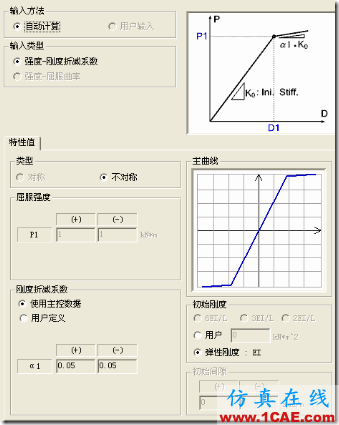
上面是双线模型的屈服面属性和MΦ曲线。

P-M关系显然就是前面的钢筋混凝土设计里的那个关系,也就是说这里的My实际就是设计结果图里的那个Mu。我们姑且不讨论这种做法是否正确,只需要验证Mu=My这个结论对不对。

对如下某单墩模型进行计算,只在墩底设一个塑性铰,计算结果见下面的图形:

结果显示屈服点在24步骤,底部剪力574.3弯矩5743.1,墩高10m,所以P=6016.16时,Pushover出来的屈服弯矩是5743.1,与P-M图里的基本一致,有所差别是因为显示的是步骤点,而实际屈服一般应该在步骤中间的某处,可见我们之前的判断是正确的。

三折线的骨架曲线确定就比较复杂一点,因为有两个屈服点,其第一屈服点P1取的是受拉区钢筋刚刚屈服时的弯矩,第二屈服点对应P2的就是P-M曲线里Mu,P1,P2都是Midas内部自动计算的。在已经知道初始有效刚度的情况下,根据P1,可以得到D1,然后根据alpha1和P2可以得到D2这样整条曲线就定义出来了,值得注意的是默认的初始刚度不能取为EI而是要用户自定义直接输入其有效刚度,而且alpha1一般也要自己计算。

3. 有效刚度的计算和使用

有效刚度=屈服弯矩/屈服曲率,屈服曲率可以按规范方法得到,但是屈服弯矩只能自己计算了。在我的软件工具里,可以使用Kent-Park的约束混凝土模型,不过最大混凝土抗压强度没有提高,也可以使用建筑混凝土规范的模型,2者使用的都是混凝土的标准强度。

首先计算Φy和Φu

Ecu=0.0074(考虑了箍筋作用)

附录里的公式

Φu=0.02324 1/m

Φy=0.002471 1/m

使用我自己开发的工具(非约束混凝土):

Φu=0.0267 1/m

Φy=0.002455 1/m

My=3085 kN.m

经过大量计算的对比,可以得出结论,使用规范附录公式计算的ΦyΦu应该是在约束混凝土本构关系下,经过简化得到的经验公式。其中Φy不仅和直径及钢筋的屈服应变有关,还和Ecu的大小,混凝土标号,弹模有很大关系,规范附录公式未考虑这些因素,估计是因为该公式预先假定了混凝土标号,比如C35或C40,Ecu则使用常规的最小体积含箍率计算等,从对比看Ecu如果考虑了箍筋作用的话,Φy不管是否考虑约束混凝土,一般都能对的比较好,但是Φu都有较大差别!

则有效刚度为:

EIeff=My/Φy=1256619 kN.m2

Midas计算出的第一屈服弯矩为

第二屈服弯矩为

软件计算的Φu 对应的弯矩3960kN.m

显然在达到Midas的破坏弯矩前,就已经达到了Φu,而导致了箍筋断裂,虽然未考虑约束混凝土对抗压强度的1.25的增大,但是结构本身由于反复荷载也会导致一定程度上强度和刚度的降低,所以使用3960作为破坏点是可以接受的。

根据软件计算可得到

Alpha1=(3960-3085)/(0.0267-0.002455)/EIeff=0.02872

Alpha2就可以随便取了,不影响结果。

4. 最大墩顶容许位移的相关计算的对比

(1)根据规范公式7.4.7计算

Du=10*10*0.002471/3+(10-10/2)*0.02324=0.198567 m

(2)根据Midas的Pushover计算:

容许转角:

Cita_u=10*(0.02324-0.2471)/2=0.103845

5. Midas的能力谱法能不能用在桥梁上

Midas的能力谱功能是建筑里原封不动转移过来,其中要求定义性能点评估办法和结构响应类型,这2者之间是有内在联系的,在建筑中,确定的方法有一张专门的表格,但显然不能套在桥梁上。从2000年后一些专门的研究看,似乎桥梁上使用强度折减系数法的比较多,包容性更好,而且结果大小适中。由于能力谱法理论比较难懂,要在设计中使用,不用Midas自带的话,就要自己开发工具。下面的例子里我就用强度折减系数法和Midas自带的这个做下粗略的比较。

四. 单柱墩顺桥向全桥Pushover

1. 算例说明:本算例是示意性的不是实际桥梁

圆形单墩,直径1.5m,墩高10m,墩底固定,墩顶质量6000kN/g。材料JTG04的C40混凝土,钢筋是20根d25的HRB335,箍筋间距0.1md16。

设计反应谱

2. 基本模型

3. 按说明要求进行钢筋混凝土构件设计,结果生成P-M图

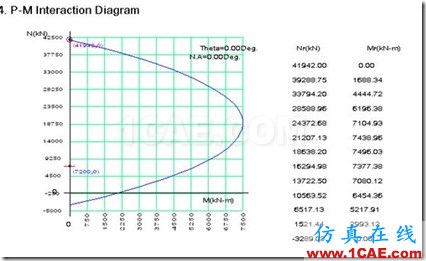
4. Pushover分析

(1)定义主控数据

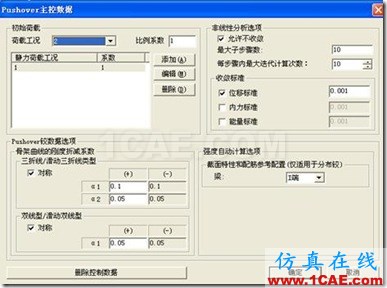
(2)定义Pushover荷载工况:

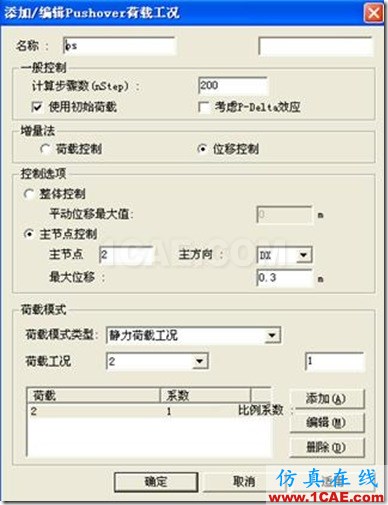
(3)定义铰

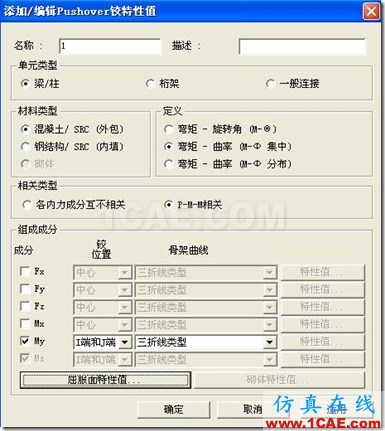
屈服面特性什么都不用改,就是默认的就可以,但是曲线形状要修改

(4)建模的最后一步就是给墩底单元分配该塑性铰,并运行计算,然后进行钢筋混凝土构件设计,在运行Pushover分析,就可以查看结果了。

5.结果

(1)第一屈服点,在步骤8

第二屈服点,在步骤128

第一屈服点软件工具计算点为3085,总的来说还是比较准确的。

第二屈服点,就是Midas自己计算的P-M图上的数值。

(2)最大容许位移,当产生0.103845的转角时为184步骤,对应位移0.276,塑性铰达到Φu时,为128步骤对应墩顶位移0.192(这个数值的计算有问题,将在1.2版本修改),选择较小值0.192作为最大容许位移。而按规范公式计算的数值是:0.1986。

屈服点步骤8对应位移:0.012

(3)底部剪力-位移曲线

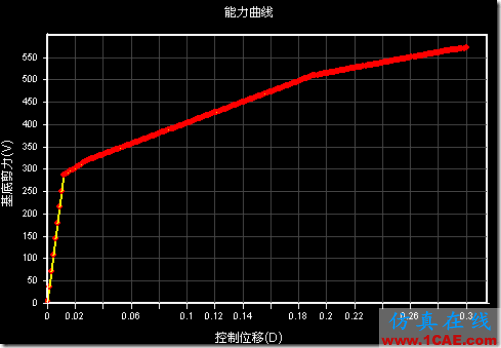
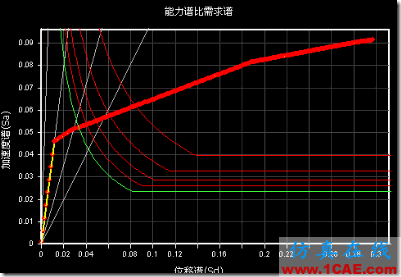
(3)性能点

反应谱

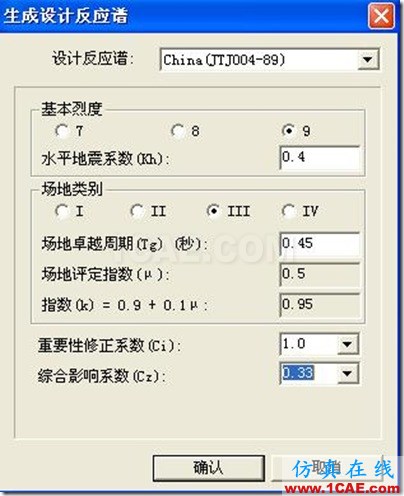
其他设置

最终的能力谱的相关曲线

性能点

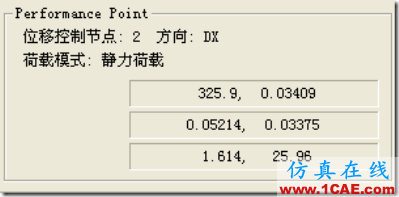
这里325.9是对应底部剪力,0.034则是其相应的墩顶位移.

位移延性比0.034/0.012=2.5

下面用我自己开发的工具计算性能点:

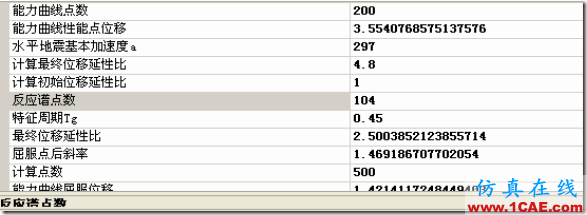
性能点位移为0.0355, 位移延性比2.5

五. 仍需要解决的问题

1. 塑性铰的长度问题

在上面的例子中,塑性铰的长度就是一个单元的长度,这显然是有问题的,这样算出来的位移要小得多。实际计算的时候应该把单元再细分些,先象上面那样定义一个单元为塑性铰,找到性能点后再根据当前弯矩决定塑性铰的长度,即超过屈服弯矩的单元都要设置塑性铰,再重新计算。

2.屈服弯矩的计算问题

“结构计算工具箱”中的计算屈服弯矩的方法还不够弯矩,其中有效刚度的没问题的,但屈服弯矩会偏大,主要是因为算法假设屈服后是平的,而实际alpha1可能会比较大,所以软件还需要完善。

3.容许位移和能力曲线屈服点的问题

上面四-5-(2)对比容许位移实际并不准确,因为增加塑性铰后位移会增大。能力曲线屈服点是Midas的计算点还是用“结构计算工具箱”的结果呢?

4.双柱墩的计算

目前看来双柱墩确实会遇到很多特别的问题,需要特别的研究。