橡胶构件abaqus+hypermesh有限元分析探讨

2017-01-23  by:CAE仿真在线  来源:互联网

1引言

有限元网格划分是进行有限元数值模拟分析至关重要的一步,它直接影响着后续数值计算分析结果的精确性。网格划分涉及单元的形状及其拓扑类型、单元类型、网格生成器的选择、网格的密度、单元的编号以及几何体素。在有限元数值求解中,单元的等效节点力、刚度矩阵、质量矩阵等均用数值积分生成,连续体单元以及壳、板、梁单元的面内均采用高斯(Gauss)积分,而壳、板、梁单元的厚度方向采用辛普生(Simpson)积分。辛普生积分点的间隔是一定的,沿厚度分成奇数积分点。由于不同单元的刚度矩阵不同,采用数值积分的求解方式不同,因此实际应用中,一定要采用合理的单元来模拟求解。

橡胶材料是一种典型的超弹材料,具有大变形、大应变及强非线性的特点。与金属类材料的小应变特性不同,大应变特性的橡胶材料在承载过程中,其结构形状会随着载荷的增加而发生改变。在模拟橡胶类材料的大变形过程中,初始设置为良好质量的单元,在变形过程中,可能会遭受扭曲,甚至严重畸变,从而导致分析程序收敛失败。因此,为改善程序的收敛性,应理解橡胶单元的变形特性,并把握好网格的整体布局,从而使网格质量在整个分析阶段都能保持较好的水平,确保计算分析成功进行。

2有限元网格划分方法

2.1网格划分的指导思想

有限元网格划分的指导思想是首先进行总体模型规划,包括物理模型的构造、单元类型的选择、网格密度的确定等多方面的内容。在网格划分和初步求解时,做到先简单后复杂,先粗后精,2D单元和3D单元合理搭配使用。为提高求解的效率要充分利用重复与对称等特征,由于工程结构一般具有重复对称或轴对称、镜象对称等特点,采用子结构或对称模型可以提高求解的效率和精度。利用轴对称或子结构时要注意场合,如在进行模态分析、屈曲分析整体求解时,则应采用整体模型,同时选择合理的起点并设置合理的坐标系,可以提高求解的精度和效率。例如,轴对称场合多采用柱坐标系。有限元分析的精度和效率与单元的密度和几何形状有着密切的关系,按照相应的误差准则和网格疏密程度,避免网格的畸形。在网格重划分过程中常采用曲率控制、单元尺寸与数量控制、穿透控制等控制准则。在选用单元时要注意剪力自锁、沙漏和网格扭曲、体积自锁等问题。

典型有限元软件平台都提供网格映射划分和自由适应划分的策略。映射划分(Mapped/IsoMesh)用于曲线、曲面、实体的网格划分方法,可使用三角形、四边形、四面体、五面体和六面体,通过指定单元边长、网格数量等参数对网格进行严格控制,映射划分只用于规则的几何图素,对于裁剪曲面或者空间自由曲面等复杂几何体则难以控制。自由网格划分(Free/Paver)用于空间自由曲面和复杂实体,采用三角形、四边形、四面体进行划分,采用网格数量、边长及曲率来控制网格的质量。例如,在MSC.MARC中,其转换(Convert)用法是几何模型转换为网格模型,点转换为节点,曲线转换为线单元,面转换为三角形、四边形等。网格自动划分(AutoMesh)则是在任意曲面上生成三角形或者四边形,对任意几何体生成四面体或者六面体。

自适应网格(adaptiveremeshing)是在每一步计算过程中,检查各单元法向来判定各区域的曲率变化情况,在曲率较大变形剧烈的区域单元,进行网格加密重新划分,如此循环直到满足网格单元的曲率要求为止。自适应网格的思想是通过网格加密的方法来提高分析的精度和效率。网格重划(solution map)是当单元发生严重扭曲变形、网格畸变导致计算不收敛时,在已经变形的几何构件上重新划分网格,再将计算结果映射回来,继续进行计算的方法。ALE(Arbitrary Lagrange-Euler)方法是Euler方法和Lagrange方法的结合,既能处理畸变动态分析问题,又能准确描述流体内部的运动。

2.2网格划分的基本方法

有限元网格划分方法有两种,对于简单的结构多采用直接建立单元模型的网格直接生成法,当对象比较复杂时,多通过几何自动生成法来完成,即在几何元素描述的物理基础上自动离散成有限单元。有限元单元可以按几何维数划分为一维、二维和三维单元,而在实际应用中采用拓扑结构单元,包括常用的质量单元、弹簧元、杆与梁管单元、平面三角形单元、平面四边形单元、膜单元、等参单元、壳单元和三维实体单元。有限元网格划分,对于二维平面、三维曲面和三维实体网格有以下几种划分方法:

(1)覆盖法:基于四边形的网格划分,要求网格划分的平面或曲面必须是完整裁减曲面,该曲面边界必须是裁减曲线;

(2)前沿法:通过把曲面等参变换到二维空间进行网格划分,然后映射到三维空间曲面上,把曲面划分成完全的四边形单元或三角形单元;

(3)Delaunay三角形法:主要用于由至少一条封闭曲线所围成的单连通域或多连通域内生成三角形单元,趋向于等边三角形。充分考虑了几何形状中细微的几何特征,并在微小特征处划分成较细的单元,在不需要密网格处,采用稀疏单元网格。

(4)转换扩展法:针对曲面几何形状比较规则的几何区域进行网格划分,其网格生成速度快,网格质量高。由节点扩展为线单元,从线单元生成平面二维单元,从二维单元生成三维单元。它不仅仅用于三维网格的生成,同时可进行一维、二维网格和几何体的生成,包括移动、镜像、拉伸、旋转、扫描三维实体的扩展方式、扩展系数和扩展方向。

3橡胶构件大变形分析的网格布局设计

3.1橡胶单元的变形特性

橡胶材料在承载过程中,结构形状会不断改变,在模拟其大变形的过程中,橡胶单元会经历这样的一个变化过程(见图1):首先是小变形、大变形,然后进入到一定量的扭曲、严重畸变甚至发展到体积为负的一个网格质量不断恶化的过程。因此,为确保有限元分析的顺利进行,应根据橡胶元件的结构特性及加载特点设置出与其相适应的网格布局。即网格布局应既能反应橡胶元件的结构特点,又能表征某一承载方式的承载特性。

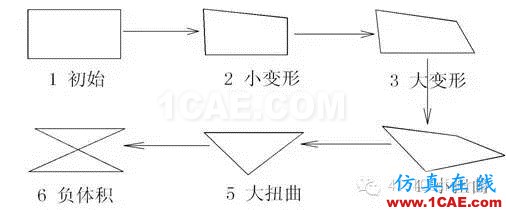
图1 网格形状的变化过程

显然,相比于相同结构下小位移问题的网格设置,大位移问题的网格布局和网格设计更加复杂,难度更大。这是因为,大位移问题的网格必须保证使单元形状在整个分析过程中是合理的。因此,为确保大位移问题的网格设计满足分析要求,应在理解元件结构及承载特性的基础上,充分预估模型的变形趋势,才能设计出有限元计算所需要的网格布局和网格质量。

3.2典型橡胶结构的网格布局设计

橡胶材料因其良好的弹性和近似不可压缩性,在密封、减振降噪等领域得到了广泛应用。橡胶材料根据使用要求,被设计成不同的结构以满足其特定的性能。而从有限元分析的角度来讲,橡胶元件的单元布局及单元形状应能适应结构形状及加载方式。根据结构形状及加载的特定方式,本文以下探讨的典型橡胶元件的单元布局及单元形状均较好地考虑了这些因素。

a圆形结构的网格布局

在橡胶密封件领域,横截面为圆形或半圆形结构的密封件使用较多,为了确保良好的密封效果,实际密封前需要对密封元件进行高度预压缩。因此在有限元分析中,为成功模拟出这种大变形下的预压缩效果,需要对密封结构进行针对其加载特性的网格布局,并最终产生环状式网格。在仿真计算中,利用这种网格布局,可以完成高达90%的变形量的分析(见图2),而如果采用普通的网格布局及单元形状,一般仅能完成 30%左右变形量的分析。

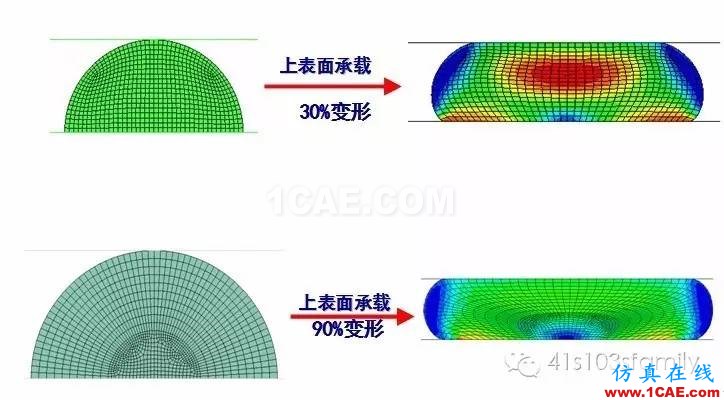
图2网格布局与分析收敛程度

b球铰结构的网格设置

橡胶球铰(见图3)是一种不同于金属关节的弹性关节,根据使用要求可设计成不同的结构形状以满足其特定功能的要求,以提供轴向、扭转、径向及偏转等六向刚度及刚度组合。从有限元分析的角度来讲,需要设计一种合适的网格布局以使由此形成的网格形状能适应各向变形及各向刚度的分析需要。图4为一种典型的分析球铰用的阶梯状网格,该阶梯状网格的优势在于可根据球铰的预压缩量及各向承载要求,参数化调整网格形状,以达到不同工况对网格的要求。因此该网格布局可适应球铰在大变形下的分析需要。

图3 橡胶球关节

图4 阶梯状网格

c锥形结构的网格特性

锥形弹簧(见图5)是一种起减振作用的橡胶弹簧,它能提供大位移量的垂向挠度,其载荷、位移特征曲线表现为较强的非线性特性。它在承载时橡胶表面变形表现为高度褶皱、自接触等复杂形态。因此,要成功模拟其承载特性及变形,设计合适的网格布局及网格形状,是完成有限元分析最为重要的环节。图6为锥形弹簧横截面上设置的放射状网格布局及单元形状,用以模拟其垂向承载特性。该放射状网格的优势在于可根据锥形弹簧垂向承载要求,适时参数化调整网格形状,以达到不同垂向承载大小对网格布局的要求。

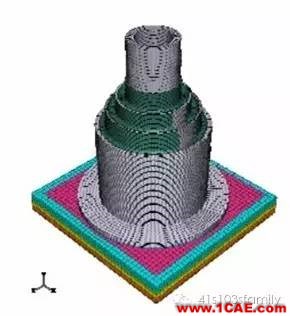
图5 橡胶锥形弹簧

图6 截面的网格布局

d堆类结构的网格设计

堆类结构(见图7)主要应用于承受垂向压缩载荷工况,其元件疲劳破坏的部位主要为橡胶与上下铁件表面的接触区域。因此,精确地模拟出橡胶部位的应力应变状态,是研究堆类结构疲劳问题的关键,而实现精确模拟的前提是设置适应结构形变的网格布局和网格形状。图8为一种典型的堆类结构有限元分析所用的层状网格,该层状网格的优势在于可根据堆类结构的垂向载荷量及结构特点,参数化调整网格形状,以适应堆类结构在垂向承载下的分析需要。

图7堆类结构

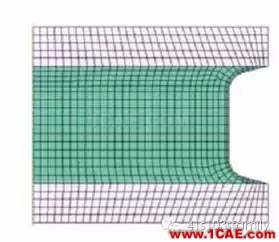
图8层状网格

4基于ABAQUS的有限元网格重划研究

良好的网格布局设计,可有效保证网格在计算分析前的较好质量。但是无法确保网格在大变形、大应变的工况下,整个的分析阶段都具有较为可靠的质量,而且当位移量继续增大时,良好的网格布局已经无法解决网格畸变所带来的问题。为确保分析能完全进行,整个分析过程中网格都具有较好质量,必须采用网格重划技术。

4.1二维网格重划技术

文献中已经详细讲述了二维网格重划的详细步骤和适应情况。图9为一简单的橡胶支座在承受正压力过程中,应用二维网格重划技术的例子。

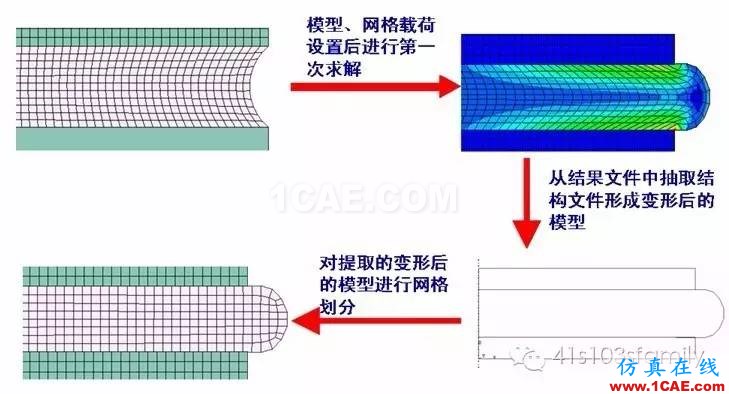
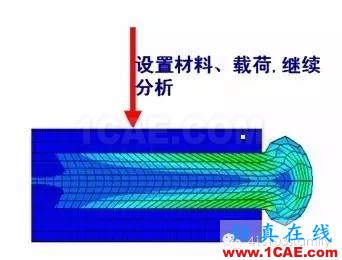
图9 二维网格重划技术应用

网格重划技术是否准确的依据是看重划前后所关心方向的刚度变化是否连续。将该橡胶支座经过二次分析所得到的完整载荷位移绘制成为一条曲线,如图10所示。

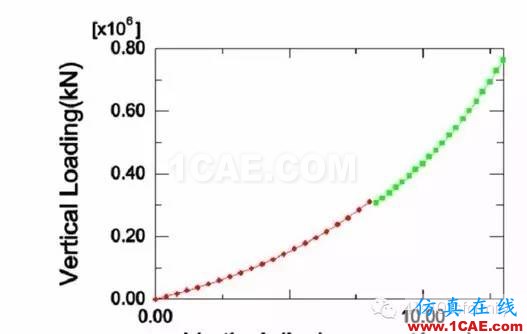
图10 元件的载荷位移曲线

如图10所示,网格重划前后的曲线没有很好的连接起来,而是存在一定的偏移,这是因为网格重划前,单元形变产生了较严重的网格畸变。这也说明,为使网格重划后的分析结果更合理,应合理确定初始分析的载荷量。这种重划方法只适用于二维几何构件。当有限元模型自身的几何构型、所受的应力状态不能简化为二维状态时,二维网格重划技术已经不再适用。

4.2三维网格重划技术

柔性接头在实际工作过程中主要受到燃烧室压强和摆动时作动力作用,可将其载荷分解为垂直增强件表面的压力和平行增强件的剪力两部分。由于双向载荷的作用,导致三维有限元模型的网格变形随着载荷增加而增大,最终网格畸变,导致计算发散。为解决弹性件橡胶材料的网格畸变问题,三维网格重划技术是一个必要途径。本文利用有限元软件对柔性接头弹性件试件进行压剪联合加载分析。成功将三维网格重划技术应用于弹性件试件应力应变状态的有限元模拟,很好的解决了双向加载中网格畸变问题,为因网格畸变而导致计算终止的三维有限元分析提供思路。

a三维网格重划过程

网格重划的基本过程见图11所示。另外,如果橡胶变形过大,则需要二次甚至多次网格重划来完成整个分析,以得到一个较准确的计算结果。

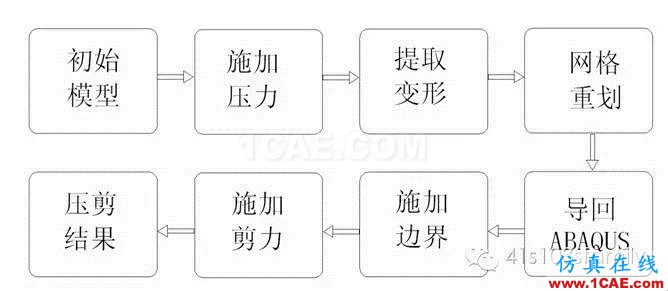
图11 网格重划的基本过程

b压剪联合网格重划计算示例

示例是一个三维橡胶板,上下两块钢板与橡胶粘接为一体,橡胶表征柔性接头弹性件,钢板表征柔性接头增强件,几何模型见图12,有限元模型见图13。有限元分析分为两个加载分析步,每个分析步时长1秒钟。第一个分析步上钢板承载垂向压力载荷,第二个分析步上钢板承受对橡胶件的水平剪力载荷。当第一个分析步结束,网格已经产生一定大变形,继续施加剪力载荷,使橡胶件网格畸变严重,计算发散。因此文中将第一分析步结束时的网格变形提取,进行网格重划。本文以ABAQUS软件为分析工具,并结合HyperMesh的强大网格划分功能,说明柔性接头弹性件橡胶材料的三维网格重划技术的全过程。

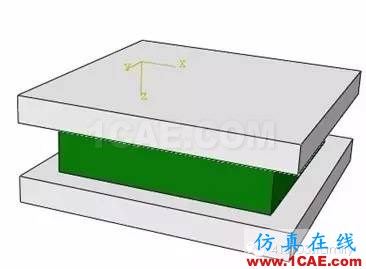
图12 试件几何模型

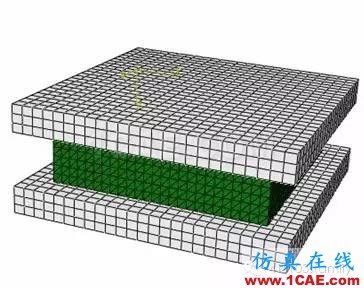
图13 试件三维有限元模型

在数值模拟过程中,要求对试件垂向加载4MPa的压强,水平施加500N的剪力。第一个分析步结束时,橡胶网格已经处于大变形状态,继续施加剪力,橡胶板网格畸变严重,计算不能收敛,此时模型中橡胶块的变形如图14所示(图中已将钢板隐藏)。由图14可见,模型中橡胶鼓出面和钢板接触边缘的网格发生了严重的畸变,网格质量检查结果为“Analysis errors:210(0.856933%),Analysis warnings:238(0.971191%)”。为使计算可以继续,在本文中利用软件HyperMesh对网格重划分,用质量好的网格代替原来的畸变网格,再将原网格上的计算结果通过Map Solution插值计算映射到新的网格上,使分析在原有结果基础上继续进行。

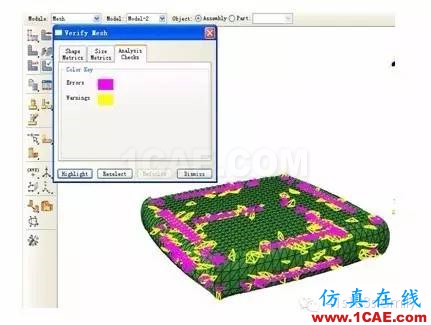
图14 垂向施加4MPa压强橡胶变形

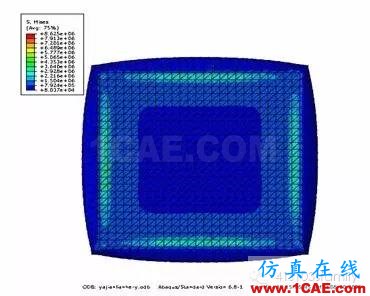
图15 橡胶垂向加载4MPa计算结果

c三维网格重划分全过程

本文利用ABAQUS/CAE中的import功能提取模型变形后的网格,在HyperMesh中读入被提取的变形网格见图16。HyperMesh可以对导入的四面体单元模型直接重划网格,利用remesh模块对旧网格范围进行重新划分网格,再将重划网格后的模型导入ABAQUS/CAE。重新划分的有限元模型如图17所示,注意尖角处的畸变网格已经得到明显改善,网格质量检查结果为“Analysis errors:0(0%),Analysis warnings:9 (0.0804%)”。

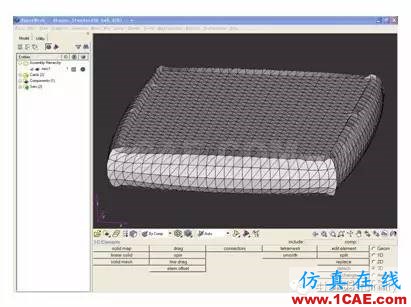
图16 4MPa压强时提取的模型

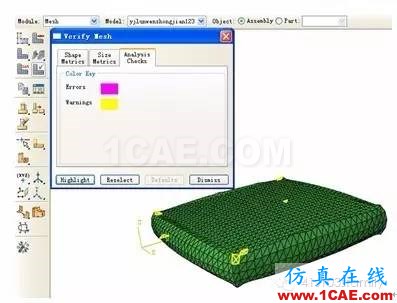
图17 重新划分网格

重新建立分析任务,比如材料属性、施加载荷等,注意本次施加水平剪力500N。写出该Job的INP,并加入*MapSolution,Step=1命令以实现映射功能,如图18所示。从ABAQUS Command中运行该INP文件,系统提示输入旧的Odb文件名,输入后Standard自动开始计算。

图18 修改INP文件

图19 将计算结果映射到新网格上

图20压剪联合计算结果

图19为将原变形网格上的计算结果映射到新网格上的结果。通过网格重划分,使水平施加500N剪力的计算任务顺利完成,图20为模型压缩剪切联合加载后的计算结果。

d结果分析

从图15与图19的比较可以发现,把原网格的计算结果映射到新网格上后,虽然结果稍有变化,但分布基本上是一致的。由于映射前后的网格不同,结果必然会有小的差异。通过合理划分网格和正确选择重划网格的载荷步,可以将差异降到最低。如果压力载荷或者剪力载荷过大,单独作用时就已经产生网格畸变,计算不收敛。可以将载荷分成几个较小的载荷步加载,进行网格重划分之后加载到预定载荷,继续计算。

5小结

对有限元网格划分方法进行了总结;设计了不同工作状态中橡胶元件的网格布局,这些布局有利于减小橡胶元件在大变形分析时的网格扭曲问题;介绍了二维网格重划技术在橡胶元件有限元分析中的应用;本文针对柔性接头的受力特点,提出了三维网格重划技术,并以表征柔性接头弹性件工作状况的试件为算例,详细阐述了这种方法的应用步骤。得到以下主要结论:

(1)橡胶材料有限元分析时经常遇到大变形收敛问题,根据结构及承载特性,设计出的反应橡胶变形的网格布局和网格形状,能够使计算得到良好的变形效果和分析结果。

(2)当橡胶材料单元畸变尤为严重时,网格布局设计已经不能解决计算不收敛的问题。此时,可以运用网格重划分技术,将加载分为几个载荷步,对变形较大模型进行重划网格,使计算继续,可以得到符合客观情况的计算结果。

(3)HyperMesh对ABAQUS四面体网格自动重划分功能可简化网格重划的步骤。同时Map Solution可以将上一步的计算结果映射到重新划分的网格上,保证了计算的连续性和结果的准确性。

相关标签搜索：橡胶构件abaqus+hypermesh有限元分析探讨 abaqus分析培训 abaqus技术教程 abaqus岩土分析 钢筋混凝土仿真 abaqus分析理论 abaqus软件下载 abaqus umat用户子程序编程 Abaqus代做 Abaqus基础知识 Fluent、CFX流体分析 HFSS电磁分析 Ansys培训