ANSYS与ABAQUS实例比较 | 矩形截面简支梁的弹塑性分析

一跨度为2米,高0.2米的矩形截面梁,在上面受到8MPa的竖直向下的均布载荷。梁的左下端是固定铰支座,右下端是滚动支座。材料为理想的弹塑性材料,弹性模量是200GPa,泊松比为0.3,屈服应力是380MPa。现在要求对该梁做静力学分析,以考察加力后梁上的应力分布,以及塑性应变。

1. 这是一个材料非线性问题,材料是理想的弹塑性。这意味着它在开始是线弹性,当越过屈服点后,应力就保持不变,而只是变形持续增加。

2. 从题目来看,该问题可以用一个平面应力问题来考虑。这就是说,忽略梁的厚度方向的应力。

1. 创建部件

二维平面应力问题,所以生成一个二维平面的部件。绘制一个矩形(2*0.2)如下图

2. 定义材料属性和截面属性

首先定义弹性属性

再定义塑性部分,当塑性应变是0时,其屈服应力是380Mpa

此时材料成为弹塑性材料

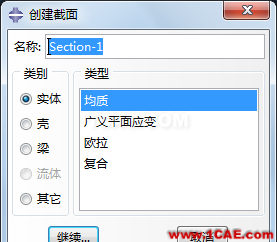
然后定义截面属性

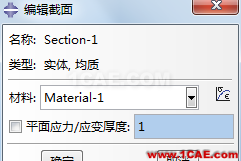
这意味着它是均质的实体截面。

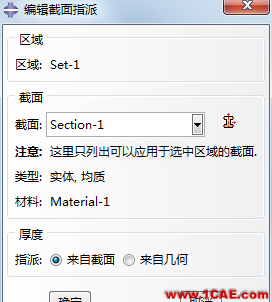
最后将该截面属性指定到部件。

3. 生成装配体

唯一的部件,根据它生成装配体。

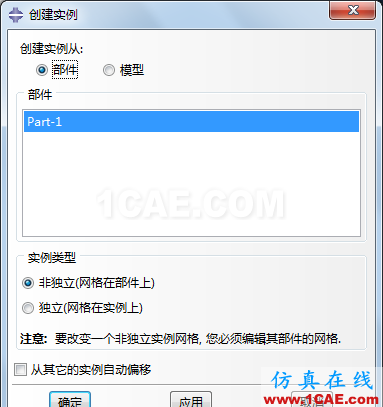
4. 创建分析步

创建一个静力学分析步。

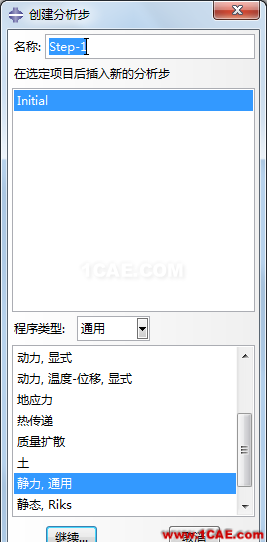
5. 定义载荷和边界条件

在初始载荷步中定义两个边界条件

(1)左下角点----固定铰支座

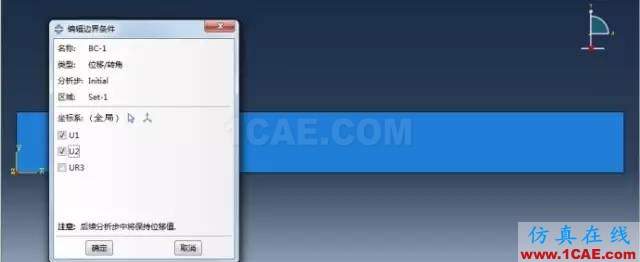
(2)右下角点----滚动支座

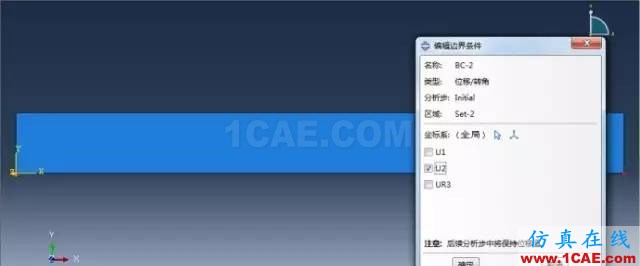
在通用静力学分析步中定义分布载荷

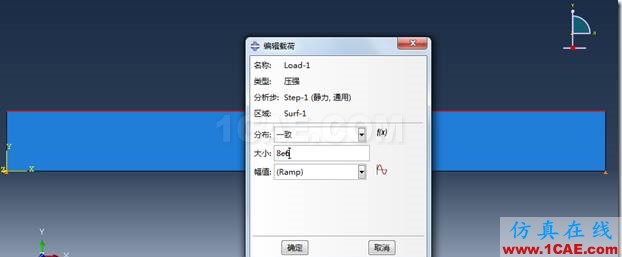
最后结果如下图

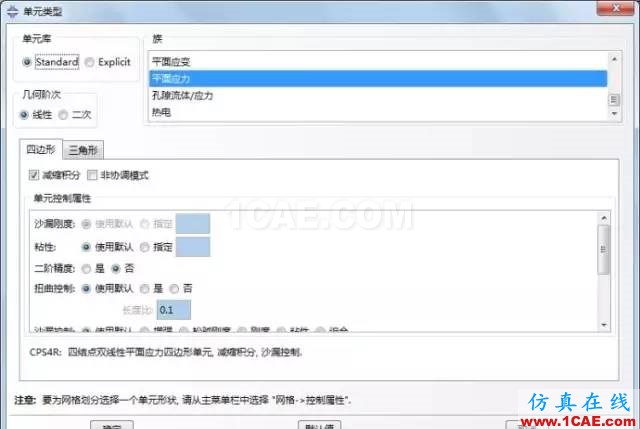
6. 划分网格

使用CPS4R平面应力单元

指定单元尺寸为0.05m

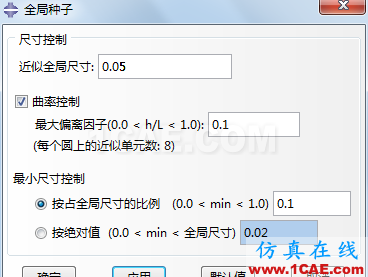
最后划分网格如下

7. 提交作业

创建作业并提交分析

8. 后处理

查看米塞斯应力

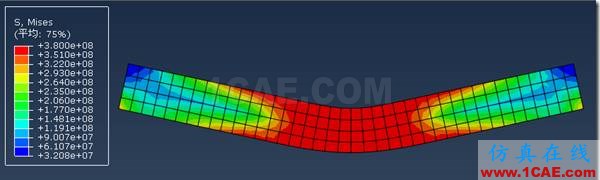
可见,中间一部分均进入到屈服状态,而两边还没有达到屈服。

查看等效塑性应变

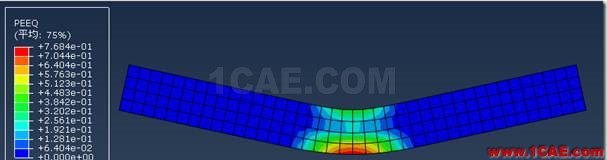
可见中间部分等效塑性应变大于0,材料发生了屈服。

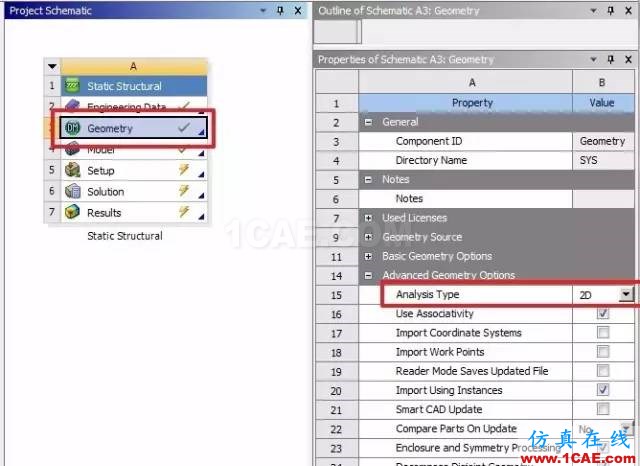
1.创建静力学分析

设置分析类型为2D分析

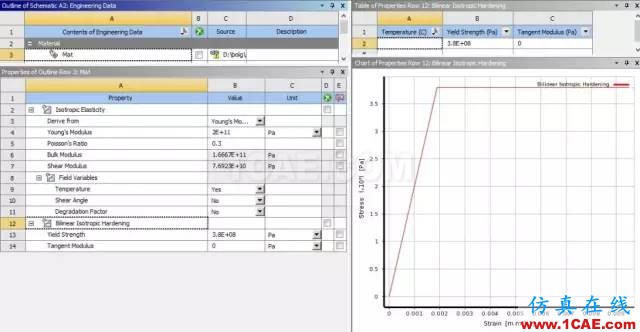
2.设置材料属性

设置弹性模量为2e11Pa,泊松比为0.3,设置塑性行为,选择塑性为双线性等向强化模型,设置屈服强度为380MPa,切线模量为0,也就是理想的弹塑性模型材料。

3.创建几何模型

创建一个 2m x 0.2m 的长方形。

4.赋予塑性材料属性

5.划分网格

设置网格尺寸为0.05m。

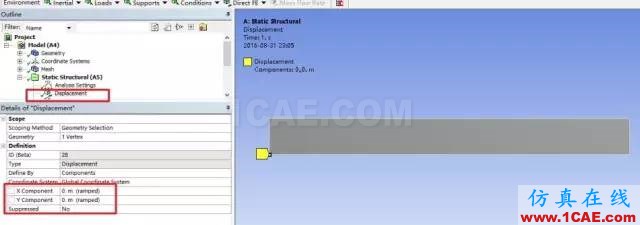
6.施加位移边界

约束左下角点的x,y方向位移和约束右下角点的y方向位移。

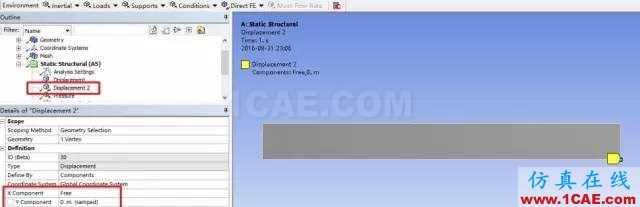
7.施加载荷边界

在上面的线上施加竖直向下的均布载荷,大小为8MPa。

8.保持默认的求解算法设置进行求解

这时,我们发现求解并不收敛,查看求解信息,我们可以看到,由于47号节点在UY的位移值为4033815.42m,该值大于软件设置的最大位移上限值,提示我们检查约束设置,可能是产生了刚性位移。然而对于这个问题来说,并不是约束不足而产生的刚性位移,而最大可能就是材料非线性的求解算法问题,但是在ANSYS中修改其他算法,皆无法求解收敛。下面将修改压力值看看是否收敛。

9.再次进行求解

减少均布压力值为6MPa,再次进行求解,这时我们发现,这次是可以求解收敛。

查看等效应力,最大值为410.47MPa。

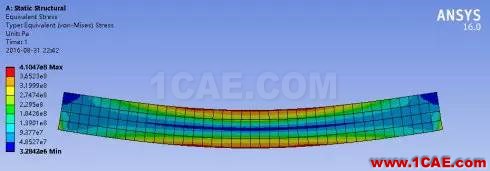
查看等效应变。

(1)在理想的弹塑性材料模型下,当施加的载荷过大时,ANSYS求解很难收敛,而ABAQUS求解容易收敛。

(2)在查看米塞斯应力时,ANSYS中最大的米塞斯应力值大于设置的屈服强度值,而在ABAQUS中最大的米塞斯应力值刚好等于设置屈服强度值,这说明二者在危险点所采用应力准则可能是不一样的,就是说,ANSYS是否是用危险点的最大正应力在与屈服应力比较,而ABAQUS则是用危险点的米塞斯应力与屈服应力在比较。

从这个实例看出,ANSYS在材料非线性求解算法方面确实没有ABAQUS算法好,当然,有可能是本人水平有限,并没有在ANSYS中找到合适的方法来求解收敛,这里欢迎各位CAE朋友多多指教!