ABAQUS小球下落问题分析
2017-05-08 by:CAE仿真在线 来源:互联网
工程结构的动力问题有两大类,一类是求结构的自振频率(固有频率)及相应的振型,另一类是求在任意动力载荷(例如冲击力、风、海浪或地震)作用下结构位置、变形或内力等随时间的变化规律。
对于线性结构,其自振频率和振型只与结构本身属性(如刚度、质量分布、约束条件等)有关、而与引起结构振动的原因无关,是结构本身的固有属性。而对于非线性结构,其动力学上的有关特性不仅与结构自身属性有关,而且与引起结构振动的原因有关。
对结构进行动力分析的目的要保证结构在使用期间,在可能发生的动力载荷作用下能够正常地工作,并确保其安全可靠。这就需要知道结构在任意动力载荷作用下随时间而变化的响应(包括位移、应变和应力等)。为此。这就需要一套有效的求解动力响应的方法。对于小型简单的动力学问题,应用相关的动力学理论知识便可解答,但对于非线性复杂的动力学分析,用理论知识求解过于繁琐也不现实,随着计算机技术的发展这类问题得到一定程度上的解决,现如今各种分析软件如:ANSYS、ABAQUS以及ADINA等。这些软件不管在静力问题还是动力问题上都能很好的应用。
本设计课题研究的是冲击方面的动力分析。冲击,顾名思义是一个结构体撞击另一个结构体的动力问题,其研究的是二物体碰撞时由于外力急速变化引起的结构物的短暂响应,控制方程和一般动力问题没有什么不同,但是在碰撞的过程中有应力波传播、局部区域的弹塑性变形、短时响应以及局部破坏等现象。如果采用数值分析方法进行求解,则要使用较小的单元网格分割,对时间间隔△T也需要取得很小。对于工程中三维问题计算费用相当大。为了应对这方面的问题,这次课题采用CAE软件辅助的办法减小计算成本以及加快计算速度。
1背景意义
1.1 背景
该课题研讨的是小球自由落体与底板碰撞的动力学分析问题,这其中存在两个可以说独立的过程,一个是自由落体过程,另一个自然是碰撞接触过程。现在分别对两种分析进行相关的介绍。
对于自由落体问题,历史上对自由落体最先研究的是古希腊的科学家亚里士多德,他提出:物体下落的快慢是由物体本身的重量决定的,物体越重,下落得越快;反之,则下落得越慢。亚里士多德的理论影响了其后两千多年的人。直到物理学家伽利略在提出了相反的意见。伽利略在1636年的《两种新科学的对话》中写道:如果依照亚里士多德的理论,假设有两块石头,大的重量为8,小的为4,则大的下落速度为8,小的下落速度为4,当两块石头被绑在一起的时候,下落快的会因为慢的而被拖慢。所以整个体系和下落速度在4-8之间。但是,两块绑在一起的石头的整体重量为12,下落速度也就应该大于8,这就陷入了一个自相矛盾的境界。伽利略由此推断物体下落的速度应该不是由其重量决定的。他在书中设想,自由落体运动的速度是匀速变化的。伽利略自由落体定律:物体下落的速度与时间成正比,它下落的距离与时间的平方成正比,物体下落的加速度与物体的重量无关,也与物体的质量无关。为了彻底改变亚里斯多德的错误所形成的影响,伽利略特意在比萨斜塔上当众用两个大小不一的铁球做了一次实验,结果让所有在场的人大吃一惊,两个铁球同时落地。亚里士多德(前384—前322年),古希腊斯吉塔拉人,世界古代史上最伟大的哲学家、科学家和教育家之一。是柏拉图的学生,亚历山大的老师。公元前335年,他在雅典办了一所叫吕克昂的学校,被称为逍遥学派。马克思曾称亚里士多德是古希腊哲学家中最博学的人物,恩格斯称他是古代的黑格尔。现在科学界对自由落体问题的认识还是从伽利略时期开始的也正是因为那个经典的落体实验推翻了亚里士多德对重物下落问题的理论。经过几百年的科学发展,无疑伽利略是对的。
碰撞,在物理学中表现为两粒子或物体间极短的相互作用。碰撞前后参与物发生速度,动量或能量改变。由能量转移的方式区分为弹性碰撞和非弹性碰撞。弹性碰撞是碰撞前後整个系统的动能不变的碰撞。弹性碰撞的必要条件是动能没有转成其他形式的能量(热能、转动能量),例如原子的碰撞。非弹性碰撞是碰撞后整个系统的部分动能转换成至少其中一碰撞物的内能,使整个系统的动能无法守恒。
两个作相对运动的物体,接触并迅速改变其运动状态的现象。可以是宏观物体的碰撞,如打夯、锻压、击球等,也可以是微观粒子如原子、核和亚原子粒子间的碰撞。经典力学中通常研究两个球的正碰,即其相对速度正好在球心的联线上。由于碰撞过程十分短暂,碰撞物体间的冲力远比周围物体给它们的力为大,后者的作用可以忽略,这两物体组成的系统可视为孤立系统。动量和能量守恒,但机械能不一定守恒。如果两球的弹性都很好,碰撞时因变形而储存的势能,在分离时能完全转换为动能,机械能没有损失,称完全弹性碰撞,钢球的碰撞接近这种情况。如果是塑性球间的碰撞,其形变完全不能恢复,碰撞后两球同速运动,很大部分的机械能通过内摩擦转化为内能,称完全非弹性碰撞,如泥球或蜡球的碰撞,冲击摆也属于这一类。介于两者之间的即两球分离时只部分地恢复原状的,称非完全弹性碰撞,机械能的损失介于上述两类碰撞之间。微观粒子间的碰撞,如只有动能的交换,而无粒子的种类、数目或内部运动状态的改变者,称弹性碰撞或弹性散射;如不仅交换动能,还有粒子能态的跃迁或粒子的产生和湮没,则称非弹性碰撞或非弹性散射。在粒子物理学中可借此获得有关粒子间相互作用的信息,是颇为重要的研究课题。
1.2 意义
前人的成果是为了让后人能有更大的成果,而作为后人不能也不会让探索世界的脚步就这样停止。对简单的自由落体问题,现如今的科学界以对其有很深的认知,然而认知无底线。由于碰撞类问题的研究日渐盛行,人们对其研究的的热情有增无减,该课题研究的就是将自由落体运动和碰撞运动结合在一起的复合运动的非线性问题。这类问题可以应用到很多类似的落体问题的现实中去,比如手机跌落,拍打篮球等行为。不同的材料,得到的结果必然不同。但是跌落类碰撞问题太多,而自己正在分析的可能是前人没有研究的在这方面的该问题的问题。希望自己对这类问题的研究能够在某种程度上起到前人的推动作用,即便微乎其微。
理论及公式
2.1 碰撞冲击问题理论知识
碰撞问题牵涉到动力学分析,它所研究的不单单是简单的静力学方面的问题,更涉及到非线性的,无限自由度的,瞬时的动力分析问题。由于篇幅限制,这里仅介绍一些简单的动力学理论,具体这方面知识可自行参考相关书籍。
2.1.1 理论分析
结构动力学分析中,把结构的质量假设为一连续的空间函数。因此结构的运动方程是一个含有空间坐标和时间的偏微分方程,只是对某些简单结构,这些方程才有可能直接求解。对于绝大多数实际结构,在工程分析中主要采用数值方法。作法是先把结构离散化成为一个具有有限自由度的数学模型,在确定载荷后,导出模型的运动方程,然后选用合适的方法求解。
2.1.2 数学模型的建立
将结构离散化的方法主要有以下三种:
集聚质量法:把结构的分布质量集聚于一系列离散的质点或块,而把结构本身看作是仅具有弹性性能的无质量系统。由于仅是这些质点或块才产生惯性力,故离散系统的运动方程只以这些质点的位移或块的位移和转动作为自由度。对于大部分质量集中在若干离散点上的结构,这种方法特别有效;
瑞利-里兹法(即广义位移法):假定结构在振动时的位形(偏离平衡位置的位移形态)可用一系列事先规定的容许位移函数f(x)之和来表示,这样,离散系统的运动方程就以广义坐标qj作为自由度。对于质量分布比较均匀,形状规则且边界条件易于处理的结构,这种方法很有效(具体类容可见结构动力学基础一书);
有限元法:可以看作是分区的瑞利-里兹法,其要点是先把结构划分成适当数量的区域(称为单元),然后对每一单元施行瑞利-里兹法。通常取单元边界上(有时也包括单元内部)若干个几何特征点(例如三角形的顶点、边中点等)处的广义位移qj作为广义坐标,并对每个广义坐标取相应的插值函数作为单元内部的位移函数(或称形状函数)。在这样的数学模型中,要求形状函数的组合在相邻单元的公共边界上满足位移连续条件。一般地说,有限元法是最灵活有效的离散化方法,它提供了既方便又可靠的理想化模型,并特别适合于用电子计算机进行分析,是目前最为流行的方法,已有不少专用的或通用的程序可供结构动力学分析之用。
动力学基本运动方程
这里也简单的对动力学基础运动方程给予简单的介绍。可用三种等价但形式不同的方法建立,即:
用达朗伯原理引进惯性力,根据作用在体系或其微元体上全部力的平衡条件直接写出运动方程;
利用广义坐标写出系统的动能、势能、阻尼耗散函数及广义力表达式,根据哈密顿原理或其等价形式的拉格朗日方程导出以广义坐标表示的运动方程;
根据作用在体系上全部力在虚位移上所作虚功总和为零的条件,即根据虚功原理导出以广义坐标表示的运动方程。对于复杂系统,应用最广的是第二种方法。
通常,结构的运动方程是一个二阶常微分方程组,写成矩阵形式为:
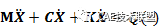 式中M、C、K、分别为质量、阻尼、刚度矩阵,X为结构的广义坐标矩阵,Q为结构的广义力矩阵。
式中M、C、K、分别为质量、阻尼、刚度矩阵,X为结构的广义坐标矩阵,Q为结构的广义力矩阵。
2.1.4 理论求解公式:
根据振动力学和结构动力学理论,我们可以计算出简支梁的固有频率和模态函数,计算过程如下:
连续梁的自由振动方程为 :
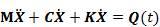 (2.1)
(2.1)
由分离变量法设:
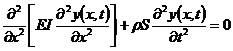 (2.2)
(2.2)
代入自由振动方程得:
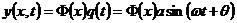 (2.3)
(2.3)
对于等截面梁:
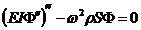 ,其中
,其中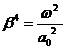 ,
,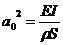 (2.4)
(2.4)
可得通解:
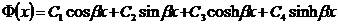 (2.5)
(2.5)
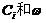 应满足的频率方程由梁的边界条件确定,对于简支梁
应满足的频率方程由梁的边界条件确定,对于简支梁
固定铰由于挠度和截面弯矩为零则在两端有:
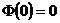 ,
,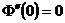
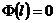 ,
, 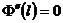 (2.6)
(2.6)
带入上式得: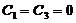 (2.7)
(2.7)
以及:
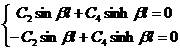

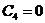 (2.8)
(2.8)
由 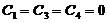 (2.9)
(2.9)
可得频率方程: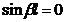

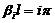 ,
,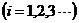 (2.10)
(2.10)
固有频率:
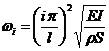 ,
,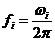
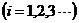 (2.11)
(2.11)
频率:
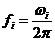 ,
, 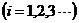 (2.12)
(2.12)
模态函数:
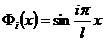 ,
,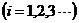 (2.13)
(2.13)
2.2 有限元法
有限元法(finite element method)是一种高效能、常用的计算方法。有限元法在早期是以变分原理为基础发展起来的,所以它广泛地应用于以拉普拉斯方程和泊松方程所描述的各类物理场中(这类场与泛函的极值问题有着紧密的联系)。自从1969年以来,某些学者在流体力学中应用加权余数法中的迦辽金法(Galerkin)或最小二乘法等同样获得了有限元方程,因而有限元法可应用于以任何微分方程所描述的各类物理场中,而不再要求这类物理场和泛函的极值问题有所联系。基本思想:由解给定的泊松方程化为求解泛函的极值问题。
2.2.1原理
将连续的求解域离散为一组单元的组合体,用在每个单元内假设的近似函数来分片的表示求解域上待求的未知场函数,近似函数通常由未知场函数及其导数在单元各节点的数值插值函数来表达。从而使一个连续的无限自由度问题变成离散的有限自由度问题。用有限个单元将连续体离散化,通过对有限个单元作分片插值求解各种力学、物理问题的一种数值方法。有限元法把连续体离散成有限个单元:杆系结构的单元是每一个杆件;连续体的单元是各种形状(如三角形、四边形、六面体等)的单元体。每个单元的场函数是只包含有限个待定节点参量的简单场函数,这些单元场函数的集合就能近似代表整个连续体的场函数。根据能量方程或加权残量方程可建立有限个待定参量的代数方程组,求解此离散方程组就得到有限元法的数值解。有限元法已被用于求解线性和非线性问题,并建立了各种有限元模型,如协调、不协调、混合、杂交、拟协调元等。有限元法十分有效、通用性强、应用广泛,已有许多大型或专用程序系统供工程设计使用。结合计算机辅助设计技术,有限元法也被用于计算机辅助制造中。
2.2.2运用步骤
步骤1:剖分:
将待解区域进行分割,离散成有限个元素的集合.元素(单元)的形状原则上是任意的.二维问题一般采用三角形单元或矩形单元,三维空间可采用四面体或多面体等.每个单元的顶点称为节点(或结点).
步骤2:单元分析:
进行分片插值,即将分割单元中任意点的未知函数用该分割单元中形状函数及离散网格点上的函数值展开,即建立一个线性插值函数
步骤3:求解近似变分方程
2.2.3发展历程
有限单元法最早可上溯到20世纪40年代。Courant第一次应用定义在三角区域上的分片连续函数和最小位能原理来求解St.Venant扭转问题。现代有限单元法的第一个成功的尝试是在 1956年,Turner、Clough等人在分析飞机结构时,将钢架位移法推广应用于弹性力学平面问题,给出了用三角形单元求得平面应力问题的正确答案。1960年,Clough进一步处理了平面弹性问题,并第一次提出了"有限单元法",使人们认识到它的功效。
50年代末60年代初,中国的计算数学刚起步不久,在对外隔绝的情况下,冯康带领一个小组的科技人员走出了从实践到理论,再从理论到实践的发展中国计算数学的成功之路。当时的研究解决了大量的有关工程设计应力分析的大型椭圆方程计算问题,积累了丰富而有效的经验。冯康对此加以总结提高,作出了系统的理论结果。1965年冯康在《应用数学与计算数学》上发表的论文《基于变分原理的差分格式》,是中国独立于西方系统地创始了有限元法的标志。
2.3 ABAQUS理论
该课题可以说部分分析是瞬态动力学分析,比如小球碰撞底板的时候。而MATKAB求解的原理也是基于有限元分析的原理对模型进行单元离散网格划分,并且对模型做一些必要的前处理。具体见相关资料说明。这里简述如下:
瞬态动力学分析需要求解半离散的方程组,离散意指结构由离散的节点描述,半离散是指在方程的导出过程中,每个时刻都要满足平衡。在瞬态分析中,连续的时间周期分为许多时间间隔,并且只有在离散的时间上才能得到解。
对于线性动力学问题,动力学行为完全由两个独立的特性决定:线弹性(动力)结构行为和施加的动力载荷。因此,可首先不考虑施加的载荷进行结构动力分析(即模态分析)来确定特征值;其次基于结构的特征值和特征模态计算给定载荷历程的结构动力响应。这一过程称为模态分析或模态叠加法。由于高阶模态不准确,因而比较成功的应用大都在于由低频范围的激振的结构。
另一种方法,动力学方程可以作为施加载荷的函数而直接积分,积分方法有多种,重要的一点就是稳定性和精度,这些方法可以用于短波长问题,只要有限元网格足够细密,就能够描述这些局部的现象。
按照求解方法,ABAQUS 允许在瞬态动力分析中包括各种类型的非线性——大变形、接触、塑性等。常用的求解方法如图2—1所示。
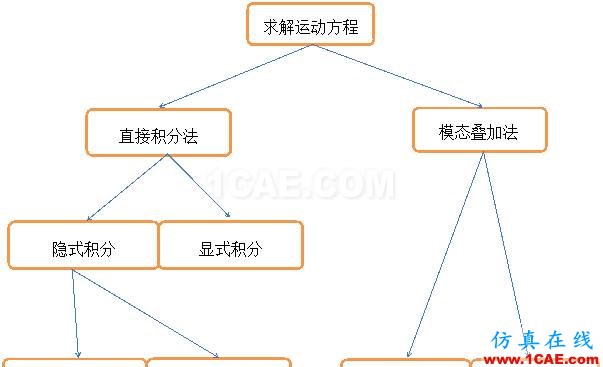
图2—1 求解方法
其中缩减矩阵和完整矩阵的主要区别是:
缩减矩阵:
用于快速求解。
根据主自由度写出[K]、[C]、[M]等矩阵,主自由度是完全自由度的子集。
缩减的[K]是精确的,但缩减的[C]和[M]是近似的。此外,还有其他一些缺陷。
完整矩阵:
不进行缩减,采用完整的[K]、[C]和[M]矩阵。
有限元分析
3.1 模型材料与几何参数
模型图见上面图3—1。下面给出具体尺寸以及材料参数:
底板:碳钢材料,密度ρ=2850kg/m3,弹性模量E=210Gpa,泊松比v=0.28;底板几何参数,底板长度x宽度=1mx1m,厚度t1=0.05m,约束情况,底板四边固定铰支。
球:橡胶材料,本构关系为Moony-Rivilin,基本参数C1=3.2MPa、C2=0.8MPa、C3=0。密度ρ=1500kg/m3,厚度t2=0.02m,内压P=0.4MPa;小球的几何参数,直径D=0.2m。
装配参数:小球放在底板正上方H=0.5m处
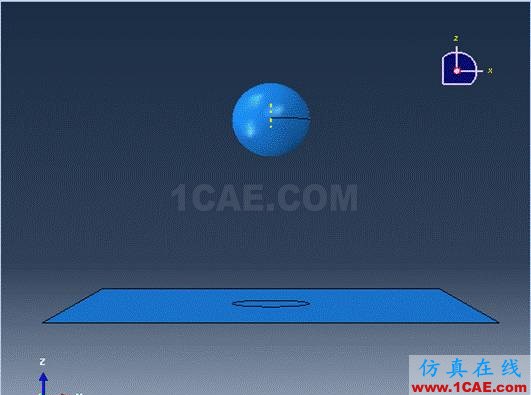
图3-1 计算模型
3.2 有限元模型的建立
由于求是密闭容器,受到外载荷的作用后,内压随变形变化,虽然常内压无法模拟这种变化,但是由于研究变内压会使得计算更加复杂而且结果不容易收敛,因此这里采用常内压进行求解计算。这里采用ABAQUS进行建模分析。
建模步骤:
-
部件的创建(这一步也可以在一些CAD软件中实施):
创建部件,用三维可变形壳造底板和球,命名。
ball:3D,Deformable,Shell,Revolution,1。轴右半圆,旋转360°。
planar:3D,Deformable,Shell,Planer,1。-0.5,-0.5; 0.5,-0.5; 0.5, 0.5; -0.5, 0.5。
-
2. 材料属性
创建材料:
将材料命名,球的材料Material-ball:密度Density:ρ=1500kg/m3;
依次操作Mechanical,Elasticity,Hyperelastic,Strain Energy potential:Mooney-Rivlin;Input Source:
Coefficients;C10=3.2MPa,C01=0.8MPa,D1=0。
将材料命名,底板材料Material-planar:密度Density:ρ=2850kg/m3;
依次操作Mechanical,Elasticity,Elastic:弹性模量E=210GPa,泊松比v =0.28。
创建截面:
球:命名为Section—ball。选中shell(壳),各项同性Honogeneous,单击Continue,在Basic中的Thickness中输入壳的厚度值Shell thickness:Value 0.02,在Material中选中之前创建的材料Material-ball,单击OK确定。
板块:命名为Section—planar。同上面选中shell(壳),各项同性Honogeneous,单击Continue,在Basic中的Thickness中输入壳的厚度值Shell thickness:Value 0.05,在Material中选中之前创建的材料Material-planar,单击OK确定。
将截面的性质附加到部件上:
球:点击Assign(或者点击快捷按钮),Section,然后选中部件ball,Done,在弹出的窗口中的Section框中选中之前创建的截面Section—ball将截面信息注入部件ball;
板块:点击Assign(或者点击快捷按钮),Section,然后选中部件planar,Done,在弹出的窗口中的Section框中选中之前创建的截面Section—planar将截面信息注入部件planar。
-
3. 装配
创建计算实体
以部件ball和planar为原形,用Dependent 方式生成实体。
装配
用旋转、平移等方法把底板放置到球的正下方。
-
创建分析步:
-
1) 创建非线性动力学分析步,命名为Step-1,Dynamic, Explicit,几何非线性(Nlgeon)打开,Δt=0.315,0~0.315s(time period 0.315),Description:The Falling Step,单击Ok确定;
-
2) 创建非线性动力学分析步,命名为Step-2,Dynamic,Explicit,几何非线性(Nlgeon)打开,Δt=0.015,0.315~0.33s(time period 0.015),Description:The Crash Step,单击Ok确定。
-
接触:
创建相互作用属性:
命名IntProp-1,属性为接触Contact,性质:无(无摩擦有限滑动),单击Ok确定。
创建接触对:
创建轮轴接触对,命名int—1在初始步Step-1 中,面-面接触Surface-to-surface contact(Explicit),主动面选球外表面,被动面选底板上表面。
-
6. 施加载荷
-
6.1 施加位移边界条件:
命名,只约束底板四边自由度ux、uy、uz。
-
6.2 创建载荷:
-
6.2.1 创建时间历程:
-
1) 历程1:平滑历程,0s:0 幅度;0.1s:1 幅度;1.0s:1 幅度;命名幅度-时间历程文件为Amp -1。顶部下拉菜单,Tools,Amplitude,Create,Amp-1,Smooth step,0,0,0.1,1,1,1。
-
2) 历程2:突变历程,0s:1 幅度;1.0s:1 幅度;命名幅度-时间历程文件为Amp -2。顶部下拉菜单,Tools,Amplitude,Create,Amp-2,Smooth step,0,1,1,1。
-
6.2.2 施加重力
顶部下拉菜单Load,命名Load—1,选择Step—1,Mechanical,重力载荷Gravity,Continue,Z方向,重力加速度Component3输入-9.8,Amplitude:Amp-1。
6.2.3 施加内压
顶部下拉菜单Load,命名Load—2,选择Step—1,Mechanical,球的内压载荷Pressure,Continue,作用于球的内壁,在Magnitude中输入0.4MPa,Amplitude:Amp-2。
-
7. 划分网格
进入Mesh模块,对部件Prat-1、Prat-2 分别进行。
-
7.1 板网格控制
-
1) 对板进行分割:将中央接触区单分区,顶部菜单Tools,Partition,Face,Sketch,选中板右边界,进入草绘界面。用绘圆工具在坐标原点做一个半径为0.1m的圆,Done;
-
2) 撒种子:顶部菜单,Seed,Edges,按住Shift键选中底板的四个边界,Done,控制种子数为3,继续选中刚刚绘制的圆,控制种子数为7,OK确定;
-
3) 划分网格:选中部件Planar,Mesh,part,Yes。
-
7.2 球网格控制
-
1) 撒种子:顶部菜单,Seed,Edges,选中部件ball的母线,Done,控制种子数为3,OK确定;
-
2) 网格控制:顶部菜单,Mesh,Controls,Tri,Free,OK确定;
-
3) 划分网格:选中部件ball,Mesh,part,Yes。
-
8. 建立项目
进入Job模块,创建项目求解。
项目:顶部菜单,Job,Create,命名Job—1,Continue,完全分析,OK确定。
计算:进入项目管理器,顶部菜单,Job,Manager,提交Submit,打开Monitor查看器观看计算过程,知道计算结束。单击Results按钮进入后处理模块,查看结果。
观察结果
利用可视化后处理模块,观察小球在下落及碰撞整个过程的应力云图及动态画面。查看接触后各帧结果的应力、位移云图以及能量变化图,分析结果数据,得到问题的结论。
3.3 结果与分析
-
3.3.1 应力云图:由于帧数有点多,这里只显示Step2中的几帧。
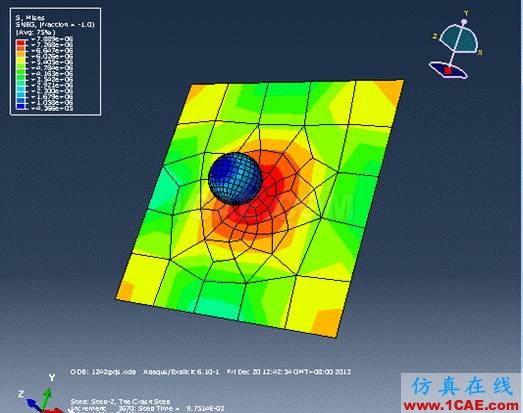 图3-2:Frame 13
图3-2:Frame 13
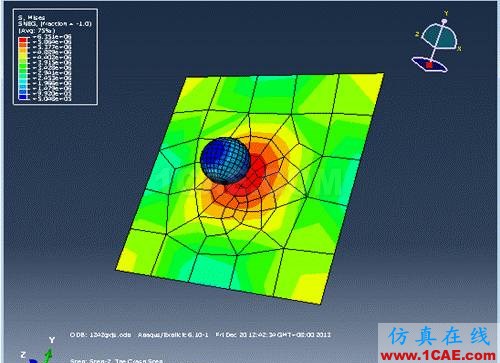 图3-3:Frame 20
图3-3:Frame 20
-
3.3.2 第二载荷步中小球模型中304号结点应力结果如下图所示:
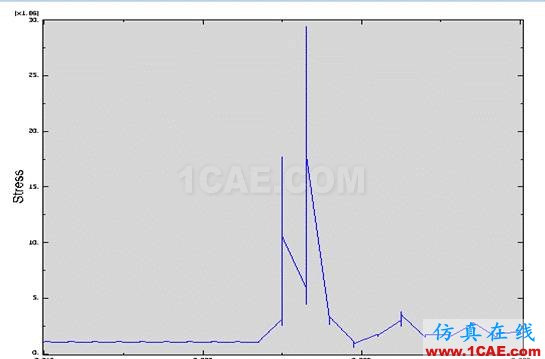 图3-4
图3-4
从该结果中可看出小球在0.322502秒之前应力值是趋于稳定阶段,可能这个阶段变形趋于稳定,应力变化不大;而过了该阶段,也就是0.3222502(s)—0.324751(s)阶段,小球接触区该结点应力变化幅度较大,最大可达到2.94507E+007Pa,可能在该阶段小球变形完全,也是自己弹性势能最大点。之后从0.324751秒之后直到结束,小球逐渐离开碰撞区,内力变化逐渐稳定,但由于弹性因素,还略有波动。
-
3.3.3 平板中间接触区某结点(80号)在Step2时应力结果
该课题所研究的是被撞底板在受到碰撞后板中的应力情况,这里只研究直接碰撞去某一结点的应力情况,研究该点最大值和应力变化情况。
曲线显示:
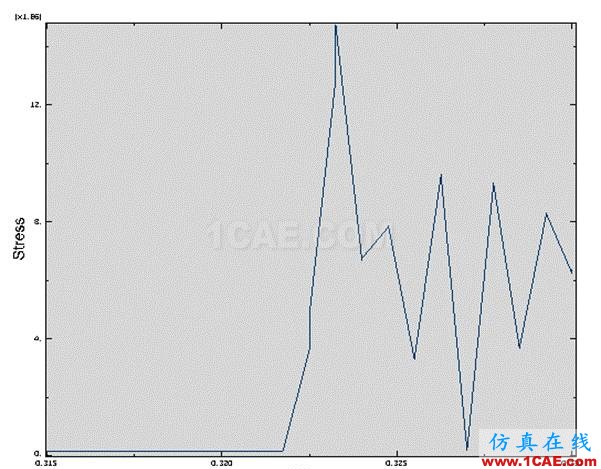 图3-5
图3-5
表格显示:
由于图表只是显示该时间段的应力变化趋势情况,具体数值情况没有很好的给出。下面给出对应上图3-6的各个具体坐标值表格如下:
表3-1
|
Time(s) |
Stress(Pa) |
|
0.315 |
164638 |
|
0.315752 |
164638 |
|
0.316501 |
164638 |
|
0.317251 |
164638 |
|
0.318 |
164638 |
|
0.318752 |
164638 |
|
0.319502 |
164638 |
|
0.320251 |
164638 |
|
0.321001 |
164638 |
|
0.32175 |
164638 |
|
0.322502 |
4.75804E+006 |
|
0.323251 |
1.4688E+007 |
|
0.324002 |
6.81925E+006 |
|
0.324751 |
7.82629E+006 |
|
0.3255 |
3.30636E+006 |
|
0.326252 |
9.65869E+006 |
|
0.327001 |
201458 |
|
0.32775 |
9.33287E+006 |
|
0.328502 |
3.71761E+006 |
|
0.329251 |
8.30387E+006 |
|
0.33 |
6.31961E+006 |
从表格数据和图形中可以看出,在0.32175秒之前板中应力状况保持不变,这段时间版中应力来源应该是版自身重力荷载所引起,如同剪支梁受局部载荷作用。在0.32175秒到最后分析结束,版中该结点应力变化成锯齿状,该过程中在0.32775秒是应力变化幅度有点大,但马上峰回路转。说明整个过程中,板中该结点应力变化是线性的,但有些模态时奇异的。另外从数据中看出该结点应力最大时刻发生在0.323251秒,Stress(MAX)= 1.4688E+007。数值相当可观。
-
3.3.4 模型在整个过程的应变能变化过程如下图所示:
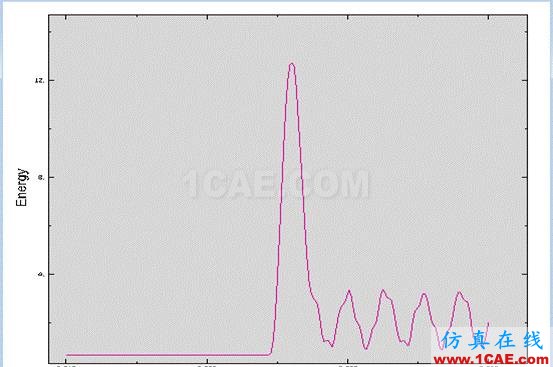
图3-6
从图中可看出,整个过程中应变能总体上是成递减状态,这也证实了碰撞能量的理论。
-
3.3.5 命令流:
*Heading
** Job name: 1242gxjs Model name: Model-1
** Generated by: Abaqus/CAE 6.10-1
*Preprint, echo=NO, model=NO, history=NO, contact=NO
** PARTS
*Part, name=ball
*Node
1, 0., 0.100000001, 0.
.........
408, 0.0203050822, -0.0978147611, -0.00446948688
*Element, type=S4R
1, 17, 18, 3, 2
........
377, 14, 15, 408, 407
*Element, type=S3
378, 17, 2, 1
.........
435, 15, 16, 408
*Nset, nset=_PickedSet5, internal, generate
1, 408, 1
*Elset, elset=_PickedSet5, internal, generate
1, 435, 1
** Section: Section-ball
*Shell Section, elset=_PickedSet5, material=Material-ball
0.02, 5
*End Part
*Part, name=planar
*Node
1, -0.5, 0.5, 0.
.........
85, -0.0259475131, 0.0442680791, 0.
*Element, type=S3
1, 68, 36, 48
………
64, 85, 76, 75
*Element, type=S4R
6, 49, 57, 69, 40
………
78, 27, 28, 83, 84
*Nset, nset=_PickedSet6, internal, generate
1, 85, 1
*Elset, elset=_PickedSet6, internal, generate
1, 78, 1
** Section: Section-planar
*Shell Section, elset=_PickedSet6, material=Material-planar
0.05, 5
** ASSEMBLY
*Assembly, name=Assembly
*Instance, name=Part-1-1, part=ball
0., 0., 0.1
*End Instance
*Instance, name=Part-2-1, part=planar
0., 0., -0.4
*End Instance
*Nset, nset=_PickedSet16, internal, instance=Part-2-1
1, 2, 3, 4, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17
18, 19, 20, 21
*Elset, elset=_PickedSet16, internal, instance=Part-2-1
7, 16, 18, 19, 22, 24, 27, 28, 32, 35, 37, 43, 47, 50, 51, 52
*Elset, elset=__PickedSurf14_SPOS, internal, instance=Part-1-1, generate
1, 435, 1
*Surface, type=ELEMENT, name=_PickedSurf14, internal
__PickedSurf14_SPOS, SPOS
*Elset, elset=__PickedSurf15_SPOS, internal, instance=Part-2-1, generate
1, 78, 1
*Surface, type=ELEMENT, name=_PickedSurf15, internal
__PickedSurf15_SPOS, SPOS
*Elset, elset=__PickedSurf17_SNEG, internal, instance=Part-1-1, generate
1, 435, 1
*Surface, type=ELEMENT, name=_PickedSurf17, internal
__PickedSurf17_SNEG, SNEG
*End Assembly
*Amplitude, name=Amp-1, definition=SMOOTH STEP
0., 0., 0.1, 1., 1., 1.
*Amplitude, name=Amp-2, definition=SMOOTH STEP
0., 1., 1., 1.
** MATERIALS
*Material, name=Material-ball
*Density
1500.,
*Hyperelastic, mooney-rivlin
3.2e+08,800000., 0.
*Material, name=Material-planar
*Density
2850.,
*Elastic
2.1e+11, 0.28
** INTERACTION PROPERTIES
*Surface Interaction, name=IntProp-1
** BOUNDARY CONDITIONS
** Name: BC-1 Type: Displacement/Rotation
*Boundary
_PickedSet16, 1, 1
_PickedSet16, 2, 2
_PickedSet16, 3, 3
** STEP: Step-1
*Step, name=Step-1
The Falling Step
*Dynamic, Explicit
, 0.315
*Bulk Viscosity
0.06, 1.2
** Name: Load-1 Type: Gravity
*Dload, amplitude=Amp-1
, GRAV, 9.8, 0., 0., -1.
** Name: Load-2 Type: Pressure
*Dsload, amplitude=Amp-2
_PickedSurf17, P, 400000.
** INTERACTIONS
** Interaction: Int-1
*Contact Pair, interaction=IntProp-1, mechanical constraint=KINEMATIC, cpset=Int-1
_PickedSurf14, _PickedSurf15
** OUTPUT REQUESTS
*Restart, write, number interval=1, time marks=NO
** FIELD OUTPUT: F-Output-1
*Output, field, variable=PRESELECT
** HISTORY OUTPUT: H-Output-1
*Output, history, variable=PRESELECT
*End Step
** STEP: Step-2
*Step, name=Step-2
The Crash Step
*Dynamic, Explicit
, 0.015
*Bulk Viscosity
0.06, 1.2
** OUTPUT REQUESTS
*Restart, write, number interval=1, time marks=NO
** FIELD OUTPUT: F-Output-1
*Output, field, variable=PRESELECT
** HISTORY OUTPUT: H-Output-1
*Output, history, variable=PRESELECT
*End Step
综合自网络
相关标签搜索:ABAQUS小球下落问题分析 abaqus分析培训 abaqus技术教程 abaqus岩土分析 钢筋混凝土仿真 abaqus分析理论 abaqus软件下载 abaqus umat用户子程序编程 Abaqus代做 Abaqus基础知识 Fluent、CFX流体分析 HFSS电磁分析 Ansys培训






