CFD逆天黑科技:“多重网格法”
2017-02-24 by:CAE仿真在线 来源:互联网
CFD的偏微分方程组离散后需要使用迭代解法来求解,比较常用的求解方法有高斯赛德尔点迭代法、雅克比点迭代法等(参考:可否认真的考虑过什么是CFD中的残差?为什么残差都是小数?)。随后,不同的Krylov子空间方法成功逆袭被应用到CFD中。
但是,Krylov子空间方法的一个致命问题即为当稀疏线性系统变得非常大的时候,收敛速度会变慢。这种迭代速率的变慢,每一步操作数的增加造成了严重的效率损失。
下图是采用普通的迭代算法求解10*10矩阵,20*20矩阵,40*40矩阵的收敛速度对比(CFD界:H.K. Versteeg在原著中并没有表示是采用了什么迭代算法...)。很明显的,40*40矩阵的收敛速度在大约100次迭代后严重放缓。
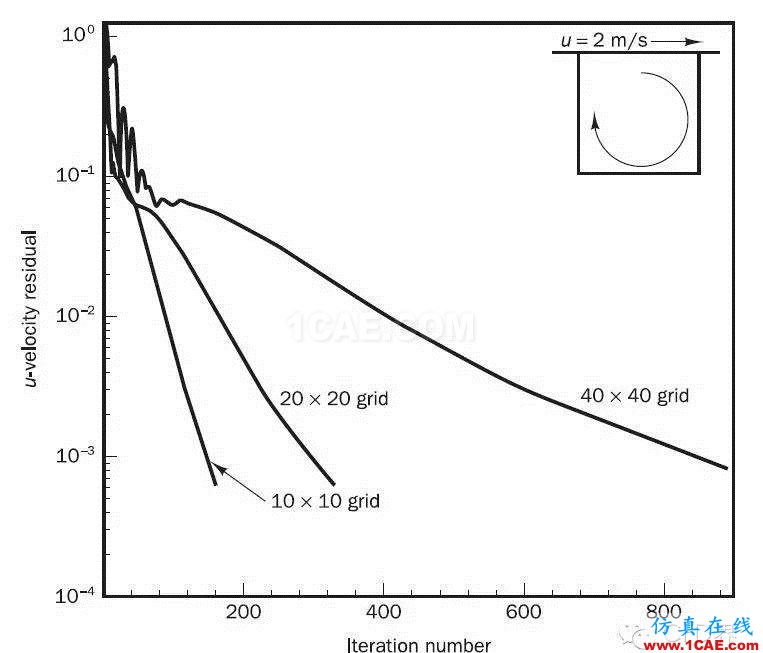
多重网格针对这种求解系统越大,收敛越慢的问题而生!
早期的多重网格方法可以追溯到60年代。然而,在70年代末和80年代初期多重网格法才出现各种变种。Brandt是多重网格的先驱者。他在多重网格中引入了各种关键技术(至今仍然广泛采用),并且和当时现存的求解方法相对比,充分的展示了多重网格法的优越性。随后,代数多重网格法被提出。
时至今日,多重网格法依然是求解椭圆PDE最有效的方法。然而,多重网格法依然存在一些缺陷,因此对多重网格法的研究从未停止。因为计算机能力越来越强,这种收敛速度和网格大小无关的算法越来越重要。
多重网格求解技术需要在不同的粗细量级的网格上对同一个原始的PDE方程进行求解。举个栗子:
-
我们首先在40*40网格上对PDE方程进行离散,然后在这个10*10网格上求解n1次
-
将PDE方程离散到20*20的网格上,进行n2次迭代
-
将PDE方程离散到10*10的网格上,进行n3次迭代
-
将10*10的网格上求得的解,重组到20*20网格,进行n4次光顺
-
将20*20的网格上求得的解,重组到40*40网格,进行n5次光顺
上述过程就完成了多重网格求解的一次循环。由于多重网格法是极为、非常、相当复杂的。关于如何正确地对方程进行操作和计算,CFD界在这里就不介绍了。
CFD大牛?一测便知
Q4:
理论上,如果计算网格无限大,不管使用什么格式,对传输方程离散后的数值解会和精确解完全一样。然而,在CFD计算中我们仅仅使用有限的、非常少的网格来计算。在这种情况下,要保持解的正确。格式需要具有以下特点:守恒性、_____、传输特性。
回复q4至CFD界获取答案
原版内容取自,额,各大CFD教材,并由CFD界整理
相关标签搜索:CFD逆天黑科技:“多重网格法” Fluent培训 Fluent流体培训 Fluent软件培训 fluent技术教程 fluent在线视频教程 fluent资料下载 fluent分析理论 fluent化学反应 fluent软件下载 UDF编程代做 Fluent、CFX流体分析 HFSS电磁分析






