FLUENT和CFX的激波分辨能力怎么样?有图有真相
2017-03-30 by:CAE仿真在线 来源:互联网
太长不看版
FLUENT的激波分辨能力优于CFX。但是,无论是FLUENT还是CFX,其激波分辨能力与激波分辨能力优秀的数值算法相比,都存在较大差距。
可压缩流动中常常存在各种间断面,如激波和接触间断等。激波的厚度是非常小的,理论计算和实际测量表明,在一般情况下,激波的厚度和气体分子的自由行程是同一个数量级的[1]。在计算流体力学软件中,激波的分辨主要采用激波捕捉(shock capturing)的方法,也就是说并不在激波位置使用局部朗金—雨贡纽条件,而是通过使用守恒形式的控制方程,在流场的基于事先构造好的网格节点的离散解答中,自动地算出激波并给出其正确的位置。为了避免激波附近的数值振荡,所使用的数值方法都含有一定的数值耗散。但是,数值耗散的存在使得原本物理上极其锋利的激波被抹平了,例如像图1所示的那样,激波的跳跃过程跨越了几个网格点,或者说激波分辨得较宽。甚至有时候,由于数值耗散太大,可以让实际上应当存在的激波在计算中消失。对于这样的数值算法,我们就说它的激波分辨能力较差。由于激波在实际应用中的重要性,激波的分辨能力成为了衡量计算流体力学软件计算精度的重要因素。
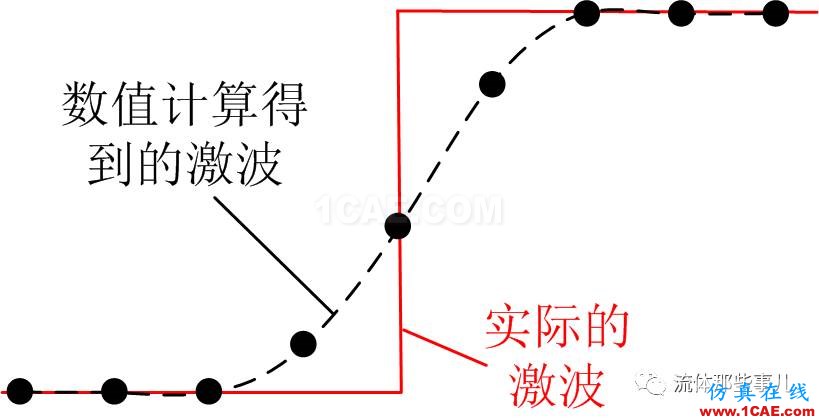
图1 激波在数值计算中被抹平
今天我们用一个算例来考验一下FLUENT和CFX的激波分辨能力。这就是经典的前向台阶激波反射流动[2]。计算域如图2所示,入口边界为均匀的马赫数Ma=3来流。注意这是一个非定常流动问题,假定在初始时刻(t=0)时全流场均为与入口边界相同的均匀流场。
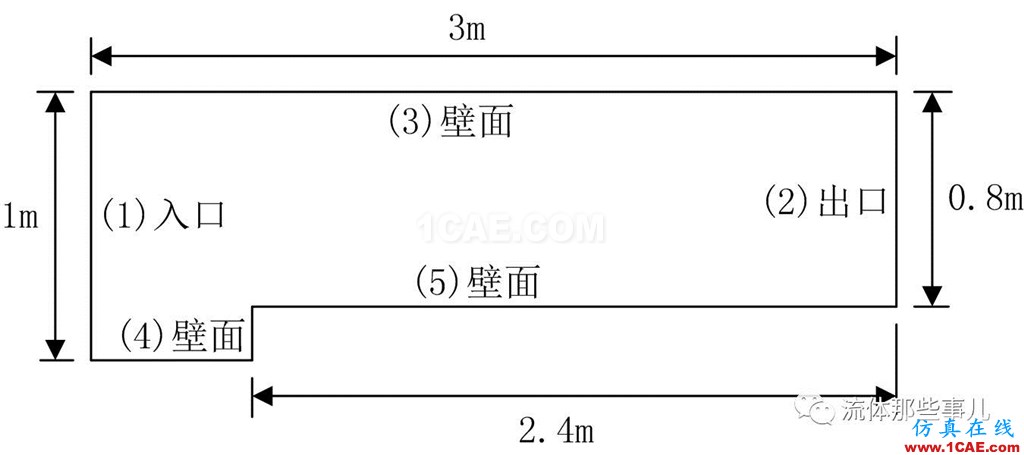
图2 计算域
计算网格等距划分,网格单元的尺寸在水平方向和垂直方向均为0.0125m,因此网格总数为16128。图3显示了计算所用的网格。
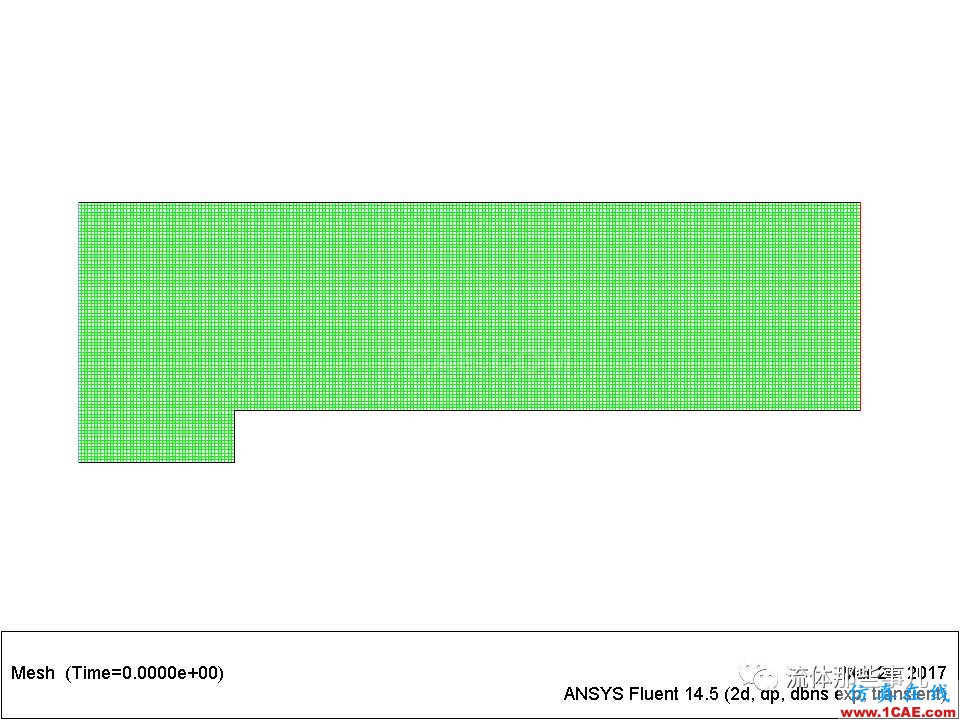
图3 网格
所用的软件版本为FLUENT 14.5和与之同期发布的CFX 14.5。下面按照FLUENT叙述主要的操作。选取基于密度的求解器。由于求解非定常流动,所以时间选项选取“瞬态”(Transient)。时间离散采用显式格式(Explicit,见图4)。
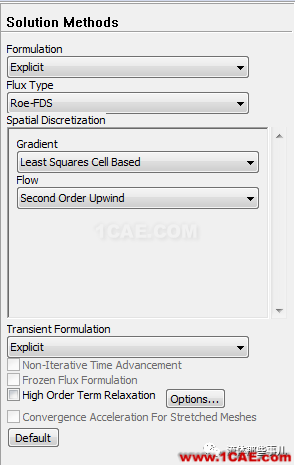
图4 时间离散
工质的状态方程使用完全气体模型(ideal-gas)。为了便于和文献[2]、[3]直接对比计算结果,将工质的定压比热(Cp, Specific Heat)设为3.5J/(kg•K),分子量(Molecular Weight)设为8314.46kg/kmol。采用无粘流动模型(Inviscid)计算。工作压力(Operating pressure)设为0。边界(1)为入口边界,使用pressure-inlet边界条件,总压(Gauge Total Pressure)设为36.73272Pa,静压(Supersonic/InitialGauge Pressure)设为1Pa。总温(Total Temperature)设为2K。注意这里入口的流动是超声速的,因此入口截面的流动状态不受下游的影响,而是由所设定的总压和静压决定。静压和总压的比值是根据入口的流动马赫数,使用气动函数[1]算出的。边界(2)为出口边界,使用pressure-outlet边界条件。由于出口截面的流动在所研究的时间范围之内都是超音速的,所以出口反压的数值对整个流场的流动实际上并没有影响,这里将反压设为0。边界(3)、(4)和(5)为壁面边界,使用wall边界条件。对于初始条件,使用入口边界的参数初始化整个流场。
在基于密度的求解器中,FLUENT提供了两种通量格式(Flux Type),即Roe和AUSM+;我们分别使用这两种格式进行计算。空间离散采用默认的二阶迎风格式(Second Order Upwind)。Courant数(Courant Number)设为0.5。由于本算例中压力、温度的数值都很小,所以要将压力和温度的下限设为0(图5)。
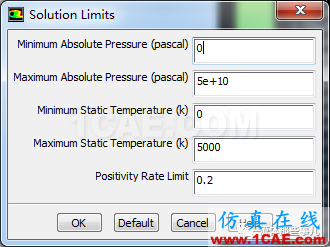
图5 变量范围的限制
计算得到的密度场演化过程如图6所示,这与文献[2]算出的密度场的演化过程(见文献[2]的图3)基本一致:t=0.5s时台阶前产生一道弓形激波;t=1s时弓形激波打在上壁面上,产生一道反射激波;t=2s的时候反射激波打在下壁面上,产生二次反射激波;t=3s的时候二次反射激波打在上壁面上,产生三次反射激波。
在CFX中,工质物性参数、边界条件、初始条件的设置可参照FLUENT的设置。对流项的离散格式(Advection Scheme)使用默认的“High Resolution”(这也是CFX理论指南[5]中考虑计算精度时推荐的格式)。CFX算出的流场演化过程大体上与FLUENT类似,这里不再给出插图。
下面我们重点观察t=4s时的流场细节(图7),由此对FLUENT和CFX的激波分辨能力进行分析。
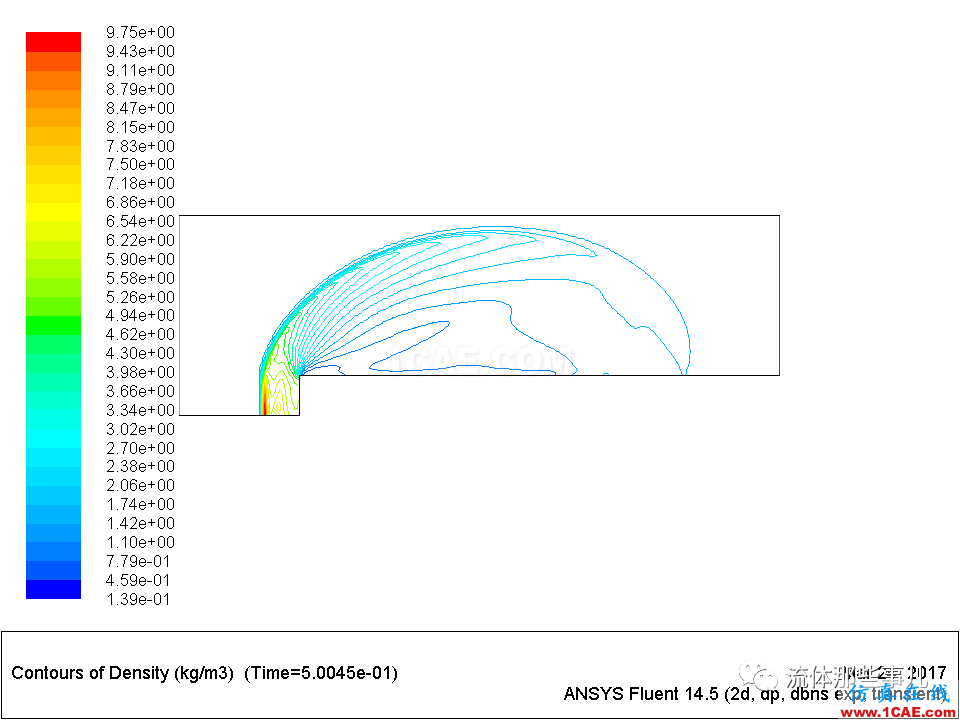
(a) t= 0.5s

(b) t= 1s

(c)t= 2s
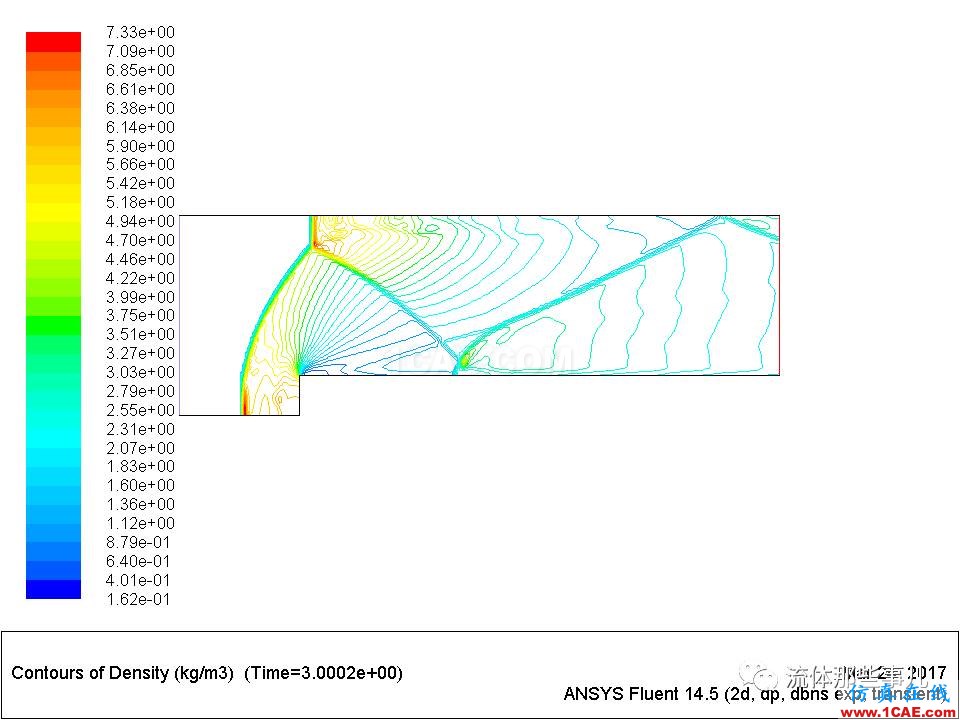
(d)t=3s

(e)t=4s
图6 计算结果(FLUENT;Roe格式)。密度等值线;等值线数量为30。
作为参考标准,我们引入了文献[3]自编程序算出的结果,即图7(a)(b),其网格密度与本文的一致。可以看出,图7(a)的流场细节与图7(b)有很大差别。由此可以看出限制器的运用对激波分辨率的决定性影响。限制器的本质就是在流场中间断面附近引入适当的数值耗散,使得这些间断面处不产生数值振荡,但是这也损害了激波分辨能力。限制器的类型有很多,其数值耗散的大小也各不相同。minmod限制器属于耗散最大的一种限制器,而superbee限制器则为耗散最小的一种限制器。由于superbee限制器的耗散非常小,所以图7(b)对整个流场结构分辨得很清晰[4]:台阶前有一弓形激波,因为其强度较大,在上壁面反射形成λ激波,波后拖出接触间断;而反射激波又在下壁面反射回上壁面,在计算域内共形成三次反射。此外流动在台阶拐角处过度膨胀,过膨胀流与台阶上壁面相撞形成一道孤立激波(图中R所示),此激波相对较弱,并与第一道反射激波异侧相交,相交后的弱激波(图中T所示)又与第二道反射激波同侧相交,相交后形成一道弱的接触间断。图7(b)的结果代表了激波分辨能力优秀的数值算法的水平。
相比之下,由于minmod限制器耗散非常大,对激波的抹平效应很大,所以图7(a)对流场结构的分辨大为逊色[4]:弱孤立激波在发展过程中被耗散掉了(图中R),与二、三次反射激波相交后的弱激波被抹平(图中T),而且在台阶上沿因数值边界层影响,二次反射形成虚假λ激波(图中S)。图7(a)的结果代表了激波分辨率较低的水平。
图7(c)为FLUENT中使用AUSM+格式的计算结果。可以看出,FLUENT的计算结果中,在台阶上二次反射形成了虚假λ激波(图中S),这与文献[3]使用minmod限制器的结果类似。可以看出弱孤立激波的存在(图中R),因此说明其激波分辨能力比文献[3]使用minmod限制器的结果强,但是与文献[3]使用superbee限制器的结果相比,这一道弱孤立激波分辨得较宽,这说明FLUENT的激波分辨率比文献[3]使用superbee限制器的结果差。弱孤立激波与第一道反射激波异侧相交后形成的弱激波也可见(图中T),但是与文献[3]使用superbee限制器的结果相比,这一道激波分辨得宽很多。
图7(d)为FLUENT中使用Roe格式的计算结果。Roe的计算结果同样存在虚假λ激波。可以看出,在FLUENT中,AUSM+格式对激波的分辨能力优于Roe格式:AUSM+格式对弱孤立激波的分辨(图7(c)中R)要比Roe格式的结果更窄。这从两者的弱孤立激波局部放大图(图7(f)和(g))可以更清楚地看出来。
图7(e)为CFX的计算结果。显然,CFX的计算结果也存在虚假λ激波。可以看出,与FLUENT相比,CFX对激波的分辨能力较差。CFX对弱孤立激波的分辨宽度虽然和FLUENT中AUSM+格式(图7(c)中R)的结果相似,但是激波的强度却要弱一些(只跨越了三条等值线)。与FLUENT中Roe格式的结果相比,激波的强度同样是较弱。这从三者的弱孤立激波局部放大图(图7(f),(g),(h))看得非常清楚。另外,在CFX的计算结果中,弱孤立激波与二次反射激波相交后的弱激波非常不明显,这一点比FLUENT中AUSM+的结果(图7(c)中T)要差。
综合上面的分析,可以看出FLUENT的激波分辨能力优于CFX;但是,无论是FLUENT还是CFX,其激波分辨能力与激波分辨能力优秀的数值算法相比,都存在较大差距。当然,好的的激波分辨能力意味着数值算法的耗散小,而耗散小则会使得算法的稳定性变差,容易计算发散。FLUENT和CFX作为商业软件,当然要更多地从用户易用性的角度考虑,所以设计算法的时候会非常重视算法的稳定性。但是,这样的软件在进行精度要求较高的机理问题研究的时候,其激波分辨率就显得不足够了。
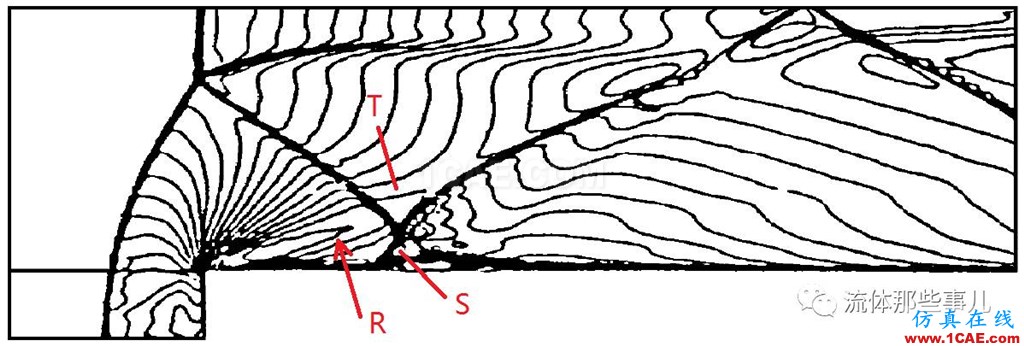
(a)文献[3],AUSM+格式,minmod限制器
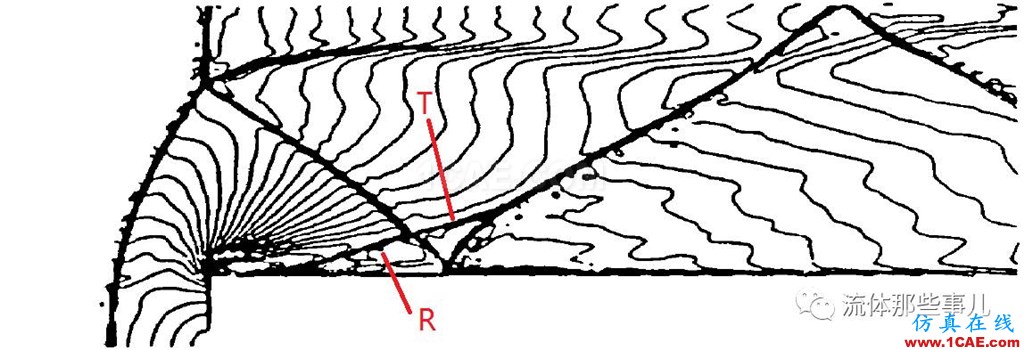
(b)文献[3],AUSM+格式,superbee限制器
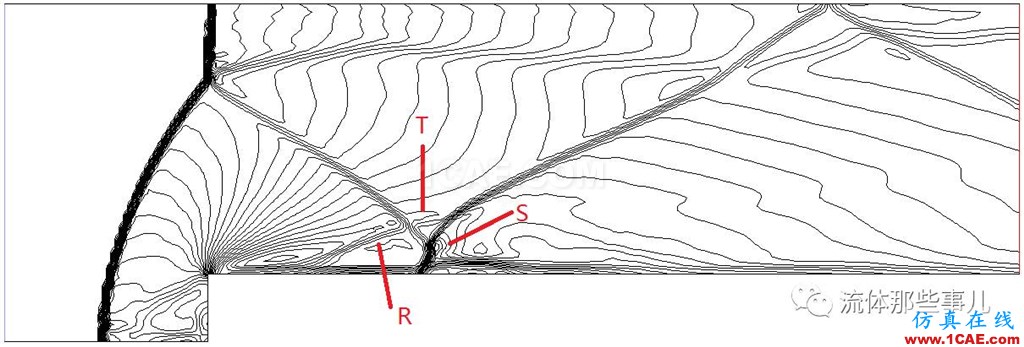
(c)FLUENT,AUSM+格式,等值线数量30
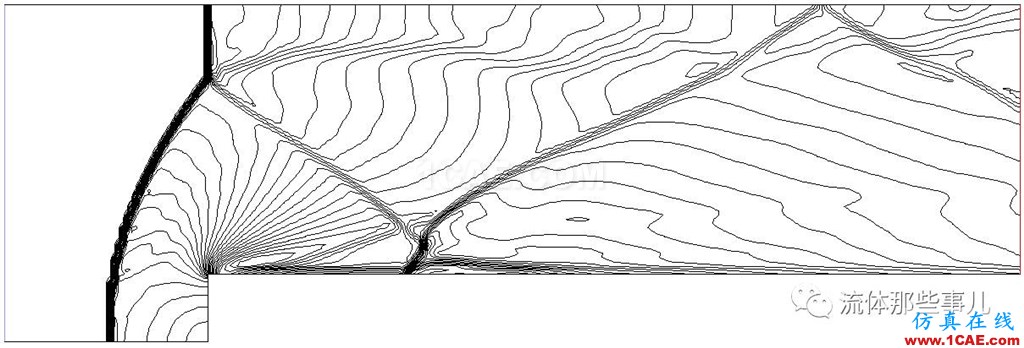
(d)FLUENT,Roe格式,等值线数量30
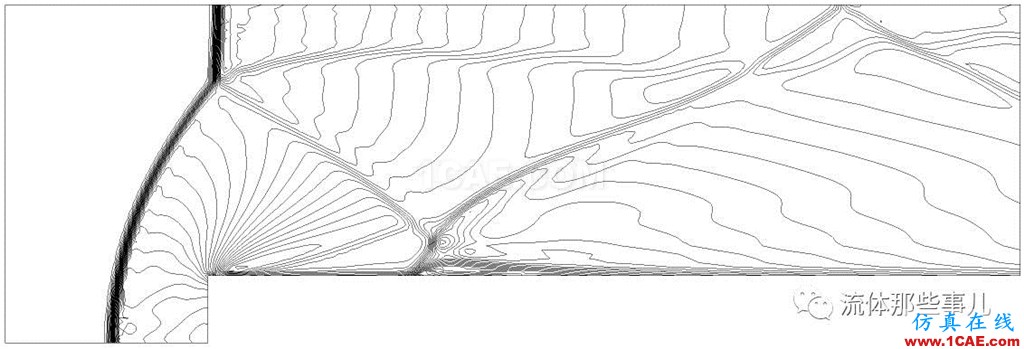
(e)CFX,等值线数量30
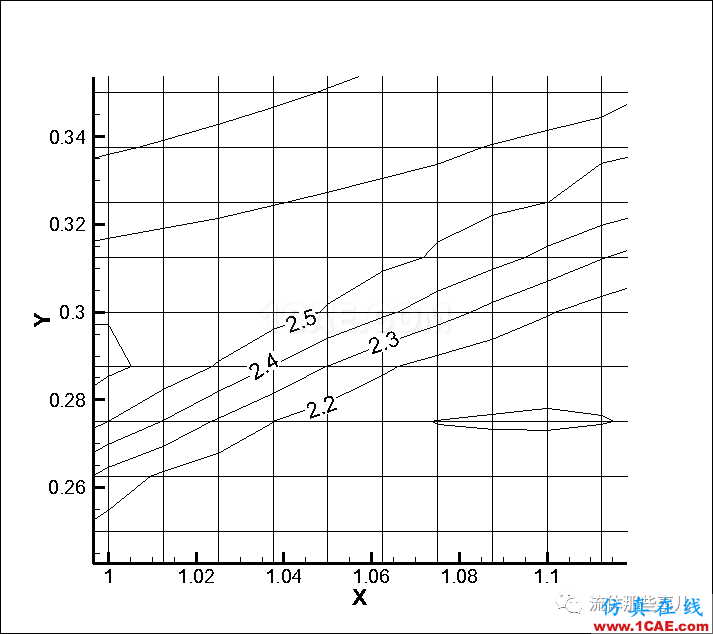
(f)FLUENT,AUSM+格式,等值线数量30;弱孤立激波局部;同时画出网格
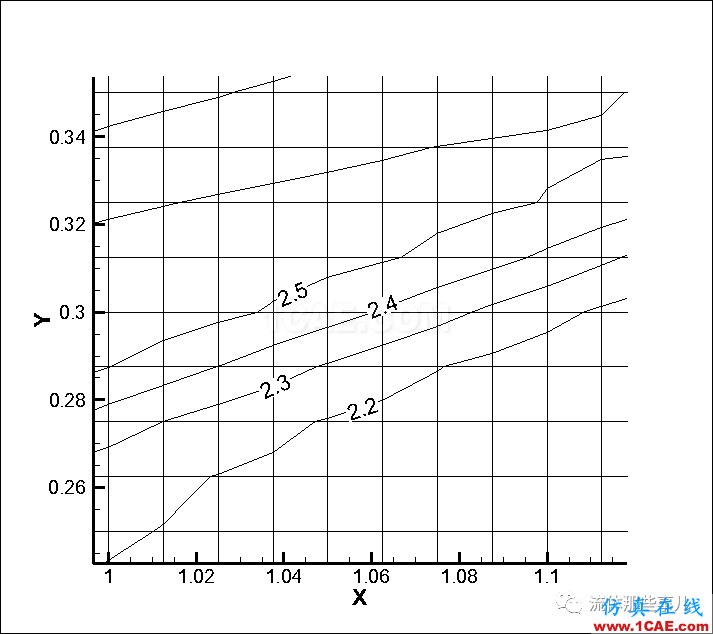
(g)FLUENT,Roe格式,等值线数量30;弱孤立激波局部;同时画出网格
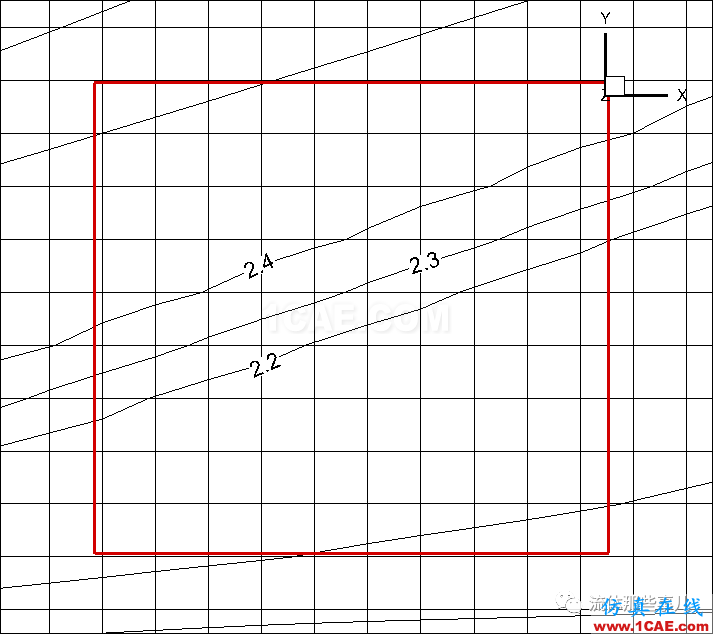
(h)CFX,等值线数量30;弱孤立激波局部;同时画出网格
图7 激波分辨率的比较。t=4;马赫数等值线。
作者感谢北京航空航天大学航空科学与工程学院的研究生靳一超。他在本文的写作上提供了很多有益的建议。
转自微信公众号:注流体那些事儿
相关标签搜索:FLUENT和CFX的激波分辨能力怎么样?有图有真相 Fluent培训 Fluent流体培训 Fluent软件培训 fluent技术教程 fluent在线视频教程 fluent资料下载 fluent分析理论 fluent化学反应 fluent软件下载 UDF编程代做 Fluent、CFX流体分析 HFSS电磁分析






