基于CFD的车辆进气系统流场仿真与分析
2017-04-24 by:CAE仿真在线 来源:互联网
针对传统发动机辅助系统中进气系统的设计多采用经验公式,结果不够准确这一问题,提出了基于计算流体动力学(computational fluid dynamics,CFD)的设计方法。通过建立进气系统的三维模型并进行网格划分,选择RNG(renormalization-gr oup)湍流模型建立气相的数学模型,定义适当的边界条件,利用Fluent 软件对进气系统气相流动规律进行数值模拟。在充分考虑空气滤清器滤网的影响,将滤网结构设为多孔介质区域的基础上,对比分析3 种设计方案内部流场的速度矢量分布和压力分布,以进气阻力为评判准则,确定进气阻力最小的方案2 为最佳设计方案。这种方法对进气系统的设计提供了实用的参考。
进气系统是车辆的重要组成部分,进气系统的性能影响着发动机和整车性能。不合理的进气系统设计导致进气阻力较大,发动机燃油经济性变差。同时进气阻力增加造成系统内部真空度加大,对系统各接口密封性提出严格的要求,当不能完全满足密封条件时,未经过滤的空气会从各接口被吸入气缸,造成气缸的磨损,减短气缸的使用寿命。
本文考虑了空气滤清器滤网的影响,针对某铰接履带运输车进气系统的几种方案,基于计算流体动力学(CFD)方法,利用成熟的流体力学软件Fluent对进气系统进行整体仿真,计算出进气系统三维湍流流场,得到内部气体的速度分布和压力分布图像,分析比较得到最优的设计方案。
模型建立
一、三维模型及网格生成
采用前处理软件gambi t 建立进气系统三维模型,由于空气滤清器结构比较复杂,在三维建模时需作适当的简化处理。建立的空气滤清器几何模型,应用gambit 进行网格划分,计算区域网格模型如图1所示。为使Fluent 处理方便、易收敛,网格划分时采用主要以六面体为主,在适当位置包含楔形网格生成体网格,在不适宜采用六面体网格部位采用非结构化四面体和锥形网格。单只空气滤清器总网格数约为43 万个。

根据发动机进气量需求及车辆具体安装空间限制,设计出3 种进气系统管路布置方案。表1 列出了3 种进气系统结构的区别。图2 表示的是3 种不同进气方案的几何模型。

二、数学模型建立

为了方便计算,提出以下假设:
1)由于进气系统工作时,气体来源于外界大气,颗粒和气体的混合物看作是一种均匀介质,它们之间没有相对滑移;在进行模拟时,可以把这种稀相气固两相流近似简化成具有平均流体特性的单相流。
2)在流动过程中密度不变,是不可压缩流体。
3)工作过程中温度不变,是等温过程。
4)空气滤清器入口的气流速度分布实际上并不均匀,在模拟时,假设入口处气流速度分布均匀。
基于以上假设,可列出进气系统内不可压缩湍流流动的控制方程组。
质量守恒方程:
连续相在计算过程中,首先要满足的是连续性方程,即质量守恒方程,任何流动问题都必须满足质量守恒定律,即
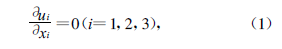
其中ui (i =1 ,2 ,3)分别为x1 ,x2 ,x3 三个方向的速度分量。
动量方程:
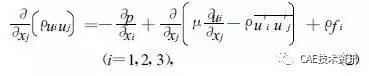
其中ρ为流体密度,p 为流体微元体上的压强,fi为3个方向的单位质量力。
式(1)、(2)中未知量个数多于方程的个数,因此是不封闭的,需要建立相应的湍流模型方程来完成封闭。
选择合适的湍流模型对仿真结果的正确性起着重要的作用。因为空气滤清器中存在着高速的旋转流场,它会使在一般情况下稳定收敛的湍流模型发散。目前应用比较普遍的有标准k -ε模型、RNG(renormalization-g roup)湍流模型和RSM (Rey n-olds stress model)模型。针对各模型优劣,有学者将其应用于旋风分离器的模拟,发现:标准k -ε模型得到的流经旋风分离器的速度矢量不准确,尤其是在中心区域,出现了一个不合理的涡流;RSM 模型得到的结果比标准k -ε模型好得多,但RSM 模型控制方程复杂,作三维仿真时不易收敛或收敛较慢;RNG 模型能较好地解决前2 种模型的不足,受到越来越广泛的关注。
RNG 模型是利用重组化群的数学方法,在标准k -ε模型基础上推导出来的,改进的湍流模型具有更高的可信度和精度。其湍动能和耗散率方程与标准k -ε模型相似,为:

式中:Gk是由于平均速度梯度引起的湍动能产生;Gb是由于浮力影响引起的湍动能产生;αk,αε分别为湍动能和耗散率的有效普朗特数的倒数,Fluent软件默认值为αk=1.0,αε=0.77 ;Prt 为湍动普朗特数,取Prt =0.85 ;β 为热膨胀系数,一般β =0.011~0.015;对高雷诺数问题,取Cμ=0.0845,默认取C1ε=1.42 ,C2ε=1.68 ,C3ε=0.09。
边界条件
操作条件:环境压力为1.01 ×10^5 Pa ,环境温度为25 ℃。
入口条件:根据进气系统进气量,定义空气滤清器进气口速度。
出口条件:主要出口(即与发动机相连出口)和空气滤清器排尘出口均设为逃逸出口条件。
壁面条件:设为无滑移壁面条件。
多孔介质区:在处理空气滤清器滤芯时,采用Fluent 中多孔介质模型。该模型适用范围非常广泛,包括填充床、过滤纸、多孔板等,其本质就是在定义为多孔介质的区域,结合了一个根据经验假设为主的流动阻力,在动量方程上叠加了一个动量源项。源项包括两部分:粘性损失项(式(5)右边第1 项)和惯性损失项(式(5)右边第2 项),即
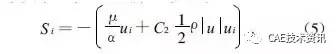
式中α为渗透性系数,C2是惯性阻力系数。根据空气滤清器厂家提供的数据,绘出一个速度与压降二次曲线,p =33.7 x2 +1.28 x 。与(5)式比较,对应系数相等,计算得到本模型的粘性阻力系数和惯性阻力系数。按实验值设定多孔介质的开孔率。
结果分析
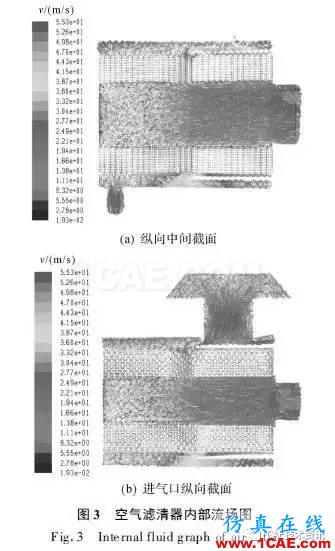
空气滤清器是进气系统的主要组成部件,也是模拟仿真的难点。为验证模拟结果真实性与准确性,对空气滤清器单独建模仿真,图3所示为空气滤清器纵向中间截面(x =0 mm)和空气滤清器进气口纵向截面(x =50.5 mm)流场示意图。从图中可以看出:气流能顺利通过多孔介质区域;在空气滤清器内部,气流速度矢量的方向和大小都有很大的改变,在出口处形成方向一致、速度较大的矢量场;在排尘口处有向外发散矢量,便于将灰尘颗粒带出空气滤清器。
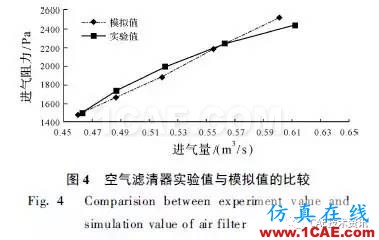
将模拟所得流速与阻力关系与实验值进行对比分析,如图4 所示。由该图可以看出,在空气滤清器正常工作范围内,模拟结果和实验结果有很好的一致性,表明多孔介质区域设置的粘性阻力系数、惯性阻力系数和开孔率符合实际,采用RNG 模型模拟的空气滤清器内部流场有良好的准确性。
根据设计好的3 种方案模型,在Fluent 中进行数值计算,得出进气系统内部的速度场与压力场。为方便比较,各方案设置相同的进气口速度,选取具有代表性的同一截面(空气滤水平中间平面)进行速度矢量分析。图5为3种方案的速度矢量图。图6为3种方案整体压力分布的压力云图。
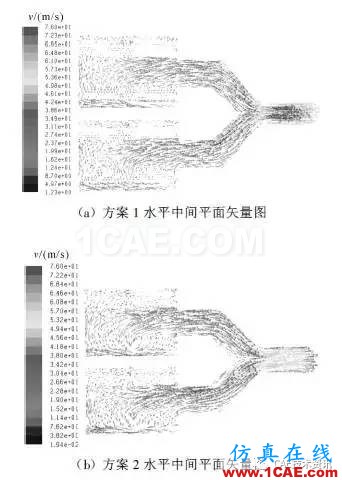

从各方案速度矢量图中可以看出:图5(a)中在两支路汇合处速度急剧升高,速度过大会对弯管产生冲击,影响接头的密封质量;图5(b)中在两支路汇合处速度变化也比较明显,但与图5(a)相比有较大改善;图5(c)显示在水平面上存在对流,气流相互撞击会造成能量损失;图5(d)显示在纵向平面内拐角处中心速度非常大,而近壁面处速度非常小,易形成涡流。
从各方案整体压力云图可以看出:图6(a)所示进气系统在两支路交汇处压力有较大变化;图6(b)与图6(c)中,同样是在两支路交汇处压力存在较大变化,但与图6(a)相比变化幅度不大;图6(a)、(b)、(c)中在折弯处均有较大负压存在,将会产生气蚀现象,造成局部的冲击,产生噪音和震动。
对进气系统进气口和出气口压力进行面积分,可以求得在不同流量下进、出气口的压力差,即进气阻力,进而得到3 种方案进气量与进气阻力之间的关系,如图7 所示。

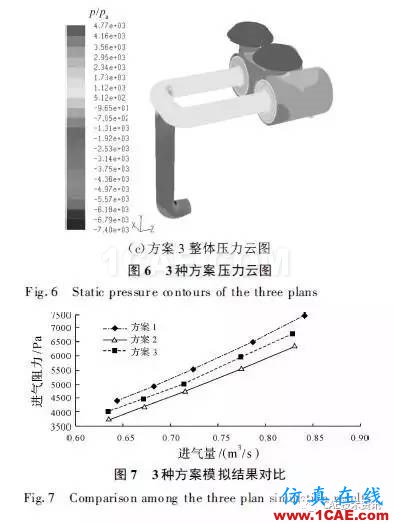
从图中可以看出:在相同进气量下,方案2进气阻力最小,方案1进气阻力最大;而在进气阻力相同时,方案2进气量最大,方案1进气量最小。
结论
1)采用合适的网格划分,设置合理的边界条件,用RNG 模型预测进气系统内流场有很好的精度。
2)用多孔介质模型计算空气滤清器滤网内部流场,能很好反映该区域的速度和压力分布,流体通过多孔介质时产生了较大的压降。
3)3 种方案中,方案2 内部流场速度变化最小,不存在对流或涡流,压力分布最均匀。
4)方案2 可以在最小的进气阻力下提供需要的进气量。
因此,通过分析Fluent 数值模拟计算结果,认为方案2为最佳设计方案。
相关标签搜索:基于CFD的车辆进气系统流场仿真与分析 Fluent培训 Fluent流体培训 Fluent软件培训 fluent技术教程 fluent在线视频教程 fluent资料下载 fluent分析理论 fluent化学反应 fluent软件下载 UDF编程代做 Fluent、CFX流体分析 HFSS电磁分析






