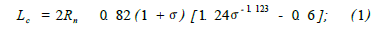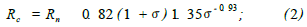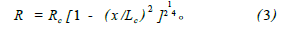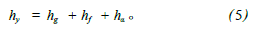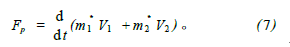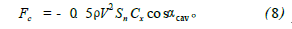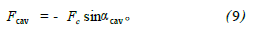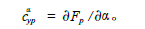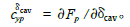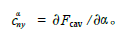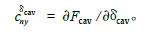为了使超空泡航行器生成满足要求的超空泡,不但在各系统功能上有特殊要求,而且在外部结构设计上也不同于普通航行器,即在超空泡航行器头部多了一个空化器,它不仅是空泡形成主要装置,同时还参与航行器的控制。由于结构的不同,决定了超空泡航行器流体动力布局的不同。航行器在超空泡形成及发展过程中经历了局部空泡到超空泡、自然空泡到通气空泡、不定常空泡到定常超空泡的过程。无论哪种过程,空泡和航行器的位置关系无外乎3种状态,即全沾湿、开式和闭合。下面就针对闭合和开式状态下航行器的受力特性进行分析。
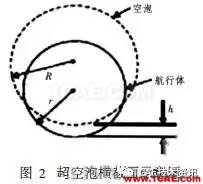
在超空泡闭合状态下,航行器几乎被空泡全包裹,沾湿部分只有头部空化器和尾部极小部分,航行器在几乎完全空化状态下运动。图1是超空泡闭合在航行器上的示意图。
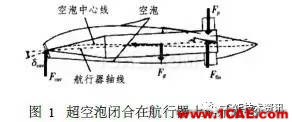
图1中δcav 为空化器舵角; Fg 为航行器重力;Fcav 为空化器的升力; Ffin 为航行器尾舵控制力; Fp为航行器尾部滑行力。
从图1中可以看出,航行器被分成了2个部分,即全包裹和半包裹。每一部分所处介质不同, 其受力特性也不同。在此,除了对常规的重力Fg 不做分析外,主要对作用在航行器上的力进行分析。
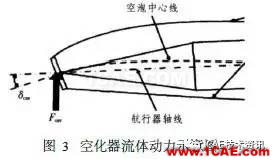
在航行器头部, 由于空化器与水接触, 产生空化器流体动力Fc ,当空化器打一个舵角时, 该力在速度系纵轴方向会产生升力Fcav。
将航行器本身所受流体动力按照空泡与航行器表面相对应关系沿纵轴方向分析如下。
对于空泡全包裹段,航行器表面充满了汽体或对于人工通气空泡则为气体,可认为气体均匀分布,则这部分航行器相当于处于气动力场中,由于气体密度远小于水的密度,因此该段航行器受到的水流体动力很小,可忽略不计。
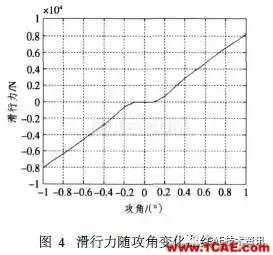
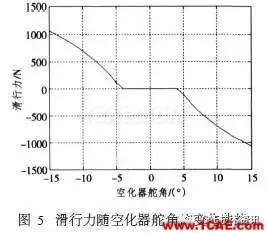
对于空泡半包裹段,航行器的一部分与水接触,另一部分与气体接触,与气体接触的压力要比与水接触压力小得多,这一部分的流体动力包括滑行力和表面粘性力等。
除了上述航行器本身的流体动力外,如果尾舵打一舵角则产生对航行器的控制力Ffin。
针对图1状态,浮力和尾舵的升力可以忽略,在纵平面内,航行器所受的流体动力只有头部空化器产生的升力和尾部在空泡壁滑行时产生的滑行力,当航行器稳定运动时,这2个流体动力与重力相平衡,这种状态是所期望的,所以超空泡航行器的大部分运行时间都处于这种状态即滑行状态。
当超空泡航行器形成自然超空泡后,开始人工通气来拉长空泡并使其趋于稳定,如果充气量过大就会使超空泡过大,没有闭合在航行器上,而是在航行器尾部敞开,这种状态即为开式超空泡。
在开式超空泡状态,航行器在纵平面内受力只有重力和作用在头部空化器的升力,显然这种状态的受力不平衡,航行器将发生倾覆,超空泡会迅速溃灭,所以这种状态持续时间不会太长。