流沙,博士,拥有近10年CFD从业经验,其编写的《ICEM CFD简明教程》在网上疯传,被学习者视为入门宝典。现已出版专著《ANSYS ICEM CFD工程实例详解》,广受好评!

本公众号将陆续推送流沙的《小白的CFD之旅》——是小说,也是CFD教程;有故事性,也有技术点;小白,也许是现在的你,亦或是曾经的你

忙碌了一个学期终于放暑假了,小白心情很愉快。然而想起CFD教材上的那些点缀着各种让人眼花缭乱符号的数学公式,整个人就不好了。不过这些事情小白也不好意思去麻烦师兄师姐们,还得靠自己去摸索。正好趁着暑假把这些东西整理一下。小白觉得最基础的CFD理论是流动控制方程,除此之外是各种数值算法。

所谓的流动控制方程,指的是流体流动过程中所需要遵循的物理规律,最常见的流动控制方程包括质量守恒方程、动量守恒方程与能量守恒方程。针对不同的流动工况,控制方程可能还包括组分守恒方程、湍流方程、状态方程等。然而对于任何流动问题,都必须遵循质量守恒方程和动量守恒方程。在非常多去的参考文献中,质量守恒方程也称之为连续方程,而把动量方程称之为纳维-斯托克斯方程,简称NS方程,CFD的任务即求解NS方程。

1 连续方程(质量守恒方程)

连续性方程比较简单。简单来讲,就是流入(流出)系统中的质量要等于系统质量的增加量(减少量)。

连续方程更严谨的表述为:

[控制体内流体质量变化率] = [穿过控制体表面的流体质量流量]

因此有:

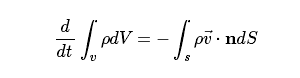
式中,n为单位法向矢量。

利用高斯散度定理(一个矢量散度的体积分应等于这个体积表面通量的面积分),即:

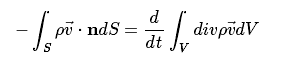
则有:

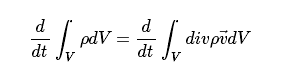
改变形式可得:

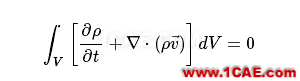
式中,

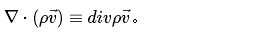
由于推导过程中对控制体形状未做任何限定,因此意味着

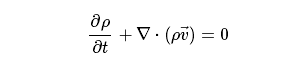
此即流动控制方程的质量守恒方程。

可展开为:

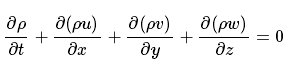
对于不可 压缩流体介质,其密度ρ为常数,则质量守恒方程可简化为:

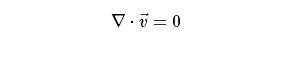
展开即为:

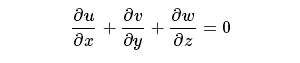
2 随体导数

随体导数是流体力学中的概念,与数学上的导数概念有差异。随体导数通常指流体微团岁时间的变化率。

随体导数用

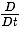
来表示。其形式为:

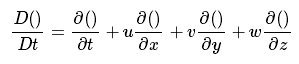
随体导数非常有用。若将单位质量通用变量记为Φ,将对时间的随体导数记为

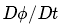
,则有:

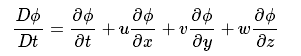
此方程定义了单位质量通用变量Φ对时间的变化率。而单位控制体体积内通用变量Φ的密度可通过密度ρ与Φ的随体导数的乘积得到,即

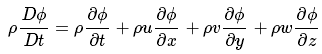
此式表示单位控制体内通用变量Φ变化率的非守恒形式。

通过质量守恒方程

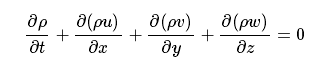
容易猜想通用变量Φ的守恒形式的各项可统一表示为:

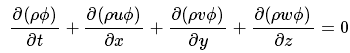
转换形式:

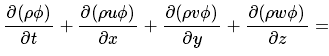
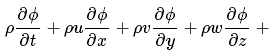
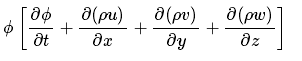
而根据质量守恒定律,有

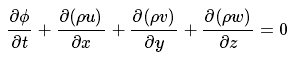
故可得:

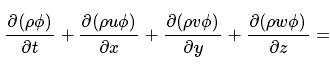
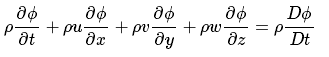
因此单位体积内Φ的变化率可表示为

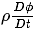
3 动量守恒方程

应用牛顿第二定律,作用在流体微团上的合力等于流体质量与加速度的乘积,即

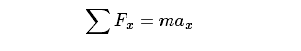
式中,Fx和ax分别为x方向上的分力与加速度。