圆柱绕流，你真的会算吗？【转发】

2017-05-01 by:CAE仿真在线来源:互联网

圆柱绕流是流体力学中的经典问题。几乎所有的流体力学教科书在讲解不可压缩无旋流动(势流)的时候,都以圆柱绕流为例分析平行流、偶极子以及点涡的组合。圆柱绕流的实际应用也非常广泛,例如桥墩、烟囱、架空电缆、换热器中的管束、飞机起落架等等。

圆柱绕流的几何形状看似简单,但是其流动图像随着雷诺数(Re=ρUD/μ,其中ρ为流体密度,U为来流速度,D为圆柱直径,μ为流体的动力粘性系数)的变化非常丰富,至今还有许多机理并未被人们认识清楚。图1是不同Re数下的圆柱绕流图像。图2是圆柱绕流阻力系数(CD=2F/ρU2A,其中F为阻力,A为迎风面积。迎风面积等于圆柱的直径乘以圆柱的长度)随Re数的变化情况。

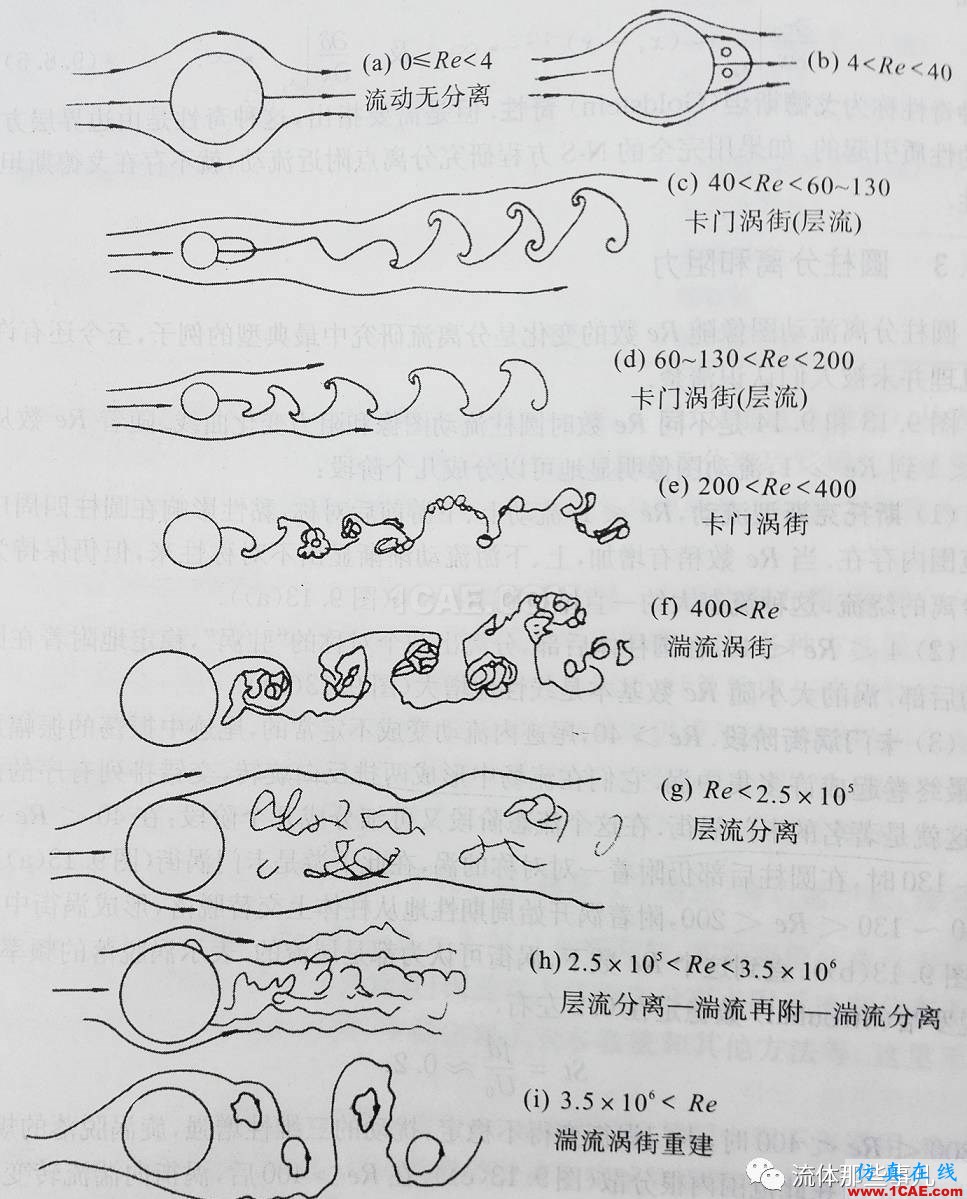
图1 不同Re数下的圆柱绕流图像。(复制自文献[1])

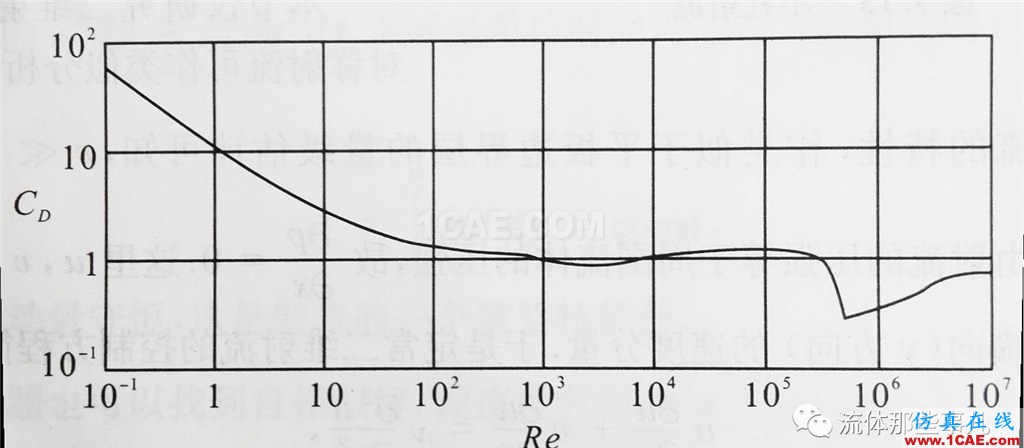
图2 圆柱绕流阻力系数随Re数的变化。实验结果。(复制自文献[1])

由于流动的复杂性,圆柱绕流的数值模拟是非常具有挑战性的课题。在最近出版的一本流体力学教科书[2]中,作者展示了圆柱绕流模拟的三个案例。使用的程序是商业软件FLUENT,模拟的雷诺数分别是150,104和107。使用二维求解器计算;由于圆柱的几何对称性,将计算域设定为一个半圆形区域(图3);使用了三种不同密度的网格:粗网格(径向30×圆周方向60)、中等网格(60×120)以及细网格(120×240)。图4是中等网格的局部放大图。三个雷诺数下都使用定常算法求解。

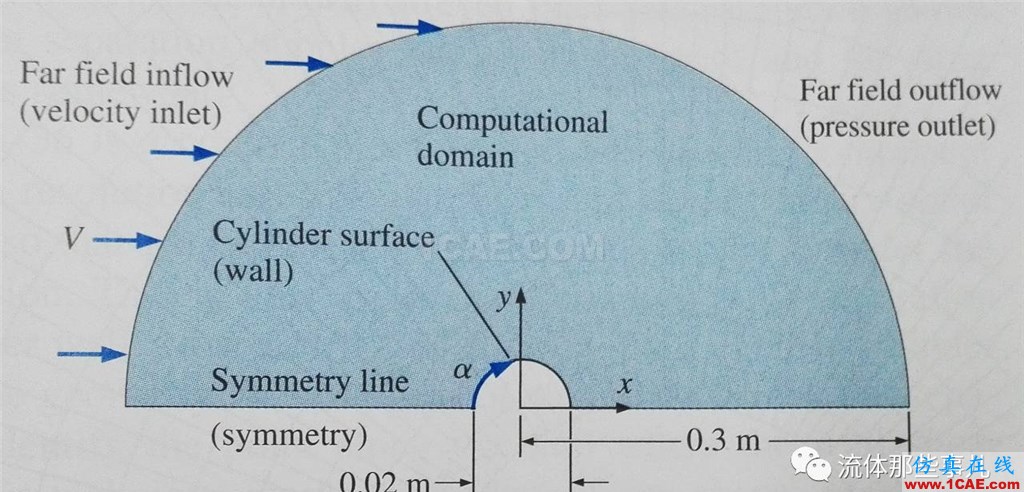
图3 计算域(复制自文献[2])

图4 中等网格(复制自文献[2])

当Re=150时,对于实验测得的阻力系数,不同文献的结果有一定差异,范围在1.1~1.4之间。实验表明这时圆柱表面的边界层是层流的,分离点位于82°的位置(图5(a)),即位于圆柱最高点的前方;尾迹也是层流的。

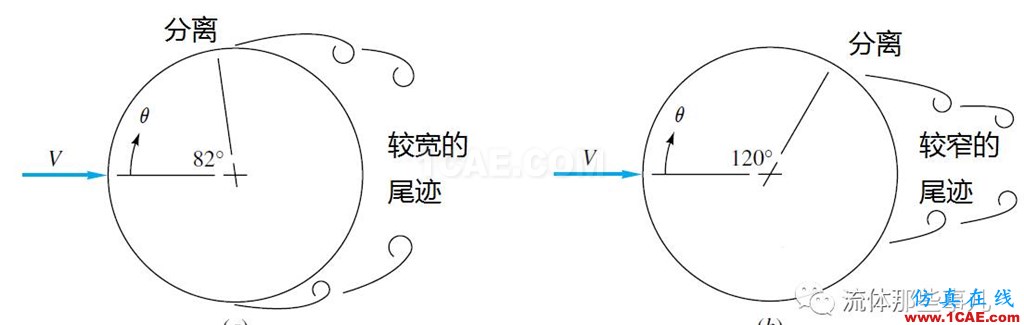
图5 分离点的位置。(a) Re=150和104; (b) Re=107

对Re=150使用层流模型计算。图6是三种不同密度网格的计算结果(流线图);三种密度的网格的计算收敛性都很好。对于图6(a)的粗网格的结果,边界层的分离点位于圆柱最高点的后方,在120°的位置,阻力系数为1.00。对于图6(b)的中等网格的计算结果,分离点稍向上游移动,位于110°的位置,似乎和实验接近了一点,但是算出的阻力系数却降低到0.982——与实验值的距离更远了。对于图6(c)的细网格的结果,外观上与中等网格的结果差异不大,分离点位于109°的位置,而阻力系数更小(0.977)。再加密网格,结果的变化就非常小了,因此可以认为已经达到网格无关。

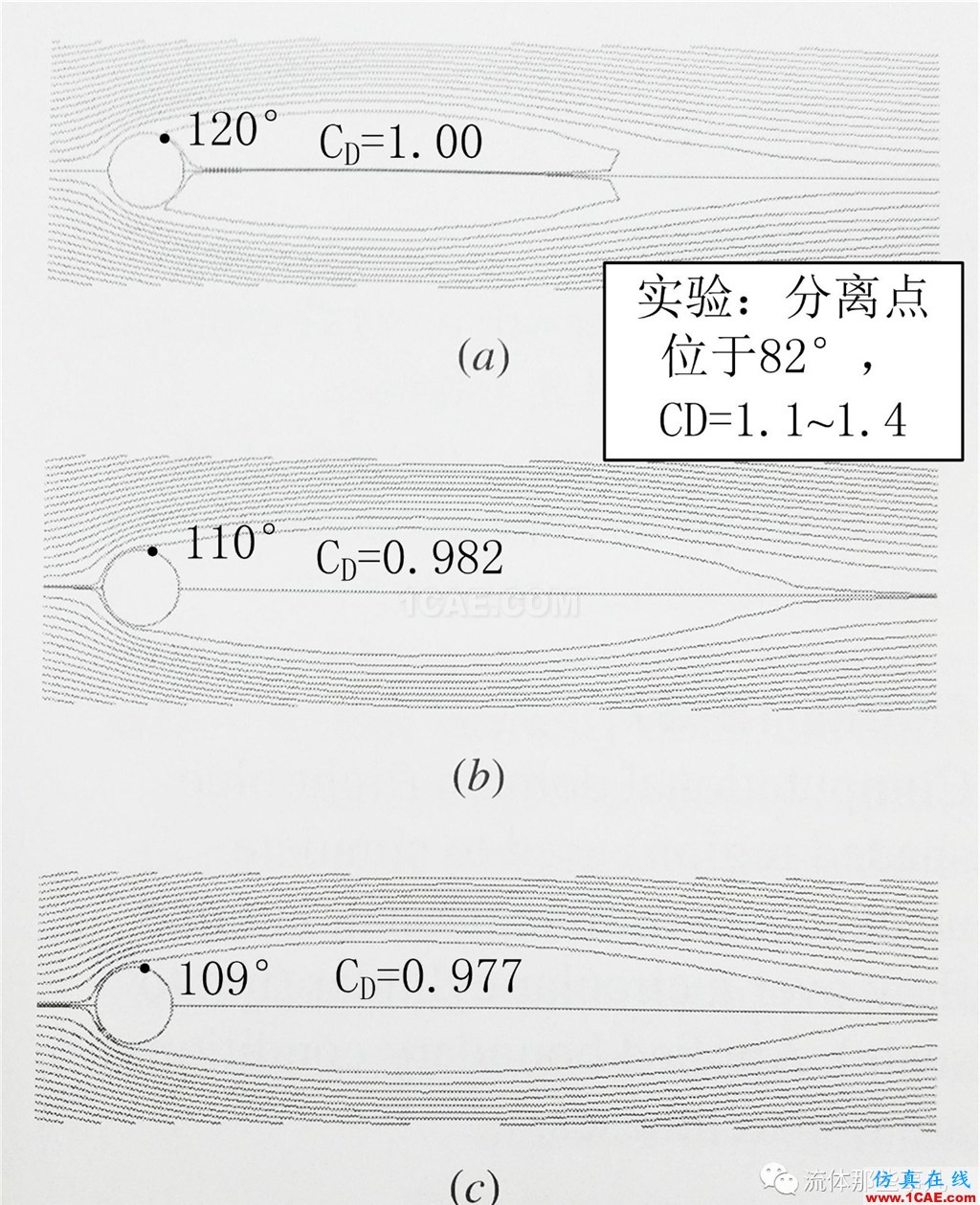
图6 Re=150的流线。(a) 粗网格;(b) 中等网格;(c) 细网格

(复制自文献[2])

显然,数值模拟结果并不符合实际。实验表明分离点位于圆柱最高点前方,在82°的位置,而数值模拟的结果中,分离点位于圆柱最高点后方,在约109°的位置。此外,数值模拟算出的阻力系数也比实验值小。

对于Re=104,实验结果表明圆柱前部的附着边界层是层流的,分离点也位于82°的位置,但是,圆柱的尾迹是湍流的;实验测得的阻力系数为1.15。这个雷诺数下使用k-ε湍流模型计算;入口的湍流度设为10%,湍流长度尺度设为圆柱直径的一半。图7是三种不同密度网格的计算结果(流线图);三种密度的网格的计算收敛性都很好。对于图7(a)的粗网格的结果,边界层分离点在圆柱顶部后方很远的地方(140°处),算出的阻力系数只有0.647,几乎比实验值小了一半。对于图7(b)的中等网格的结果,分离点前移到104°的位置,阻力系数增加到0.742——虽然离实验值近了一些,但是仍然显著小于实验值。对于图7(c)的细网格的结果,与中等网格的结果非常相似,阻力系数为0.753,分离点位于102°的位置。可以看出,这次数值模拟结果仍然不符合实际;分离点的位置与实验不符,阻力系数也显著小于实验值。

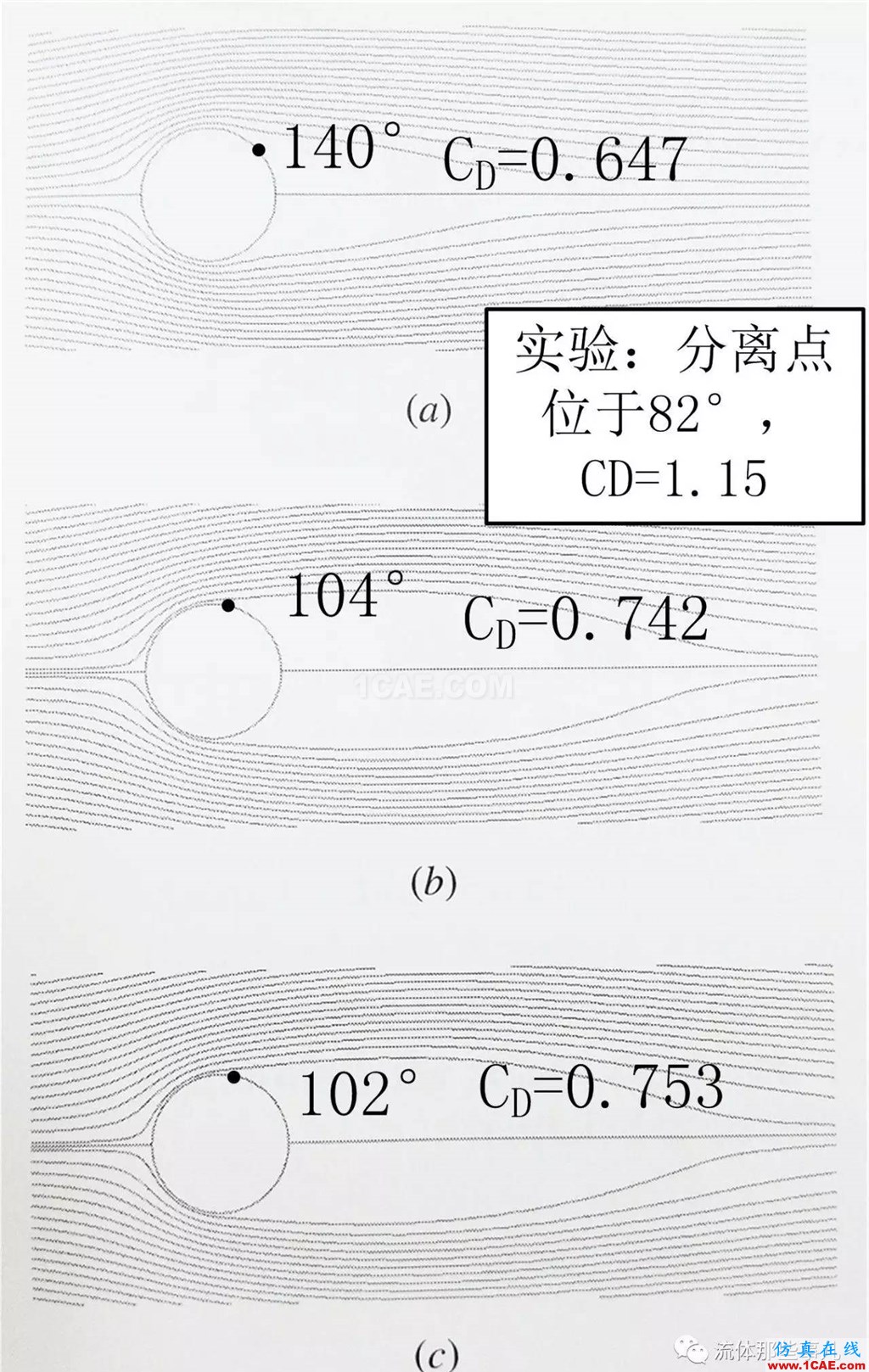
图7 Re=104的流线。 (a) 粗网格;(b) 中等网格;(c) 细网格

(复制自文献[2])

对于Re=107,实验结果表明圆柱表面的附着边界层是湍流的(头部驻点附近除外),尾迹当然也是湍流的;分离点位于圆柱最高点后方,在120°的位置(图5(b));阻力系数为0.7。这个雷诺数的流动同样使用k-ε湍流模型计算。网格的密度与前述的细网格相似,但是在壁面附近按照湍流模拟中近壁面网格的要求进行加密(因为这时雷诺数很高,边界层很薄);与Re=104时一样,入口的湍流度设为10%,湍流长度尺度设为圆柱直径的一半。不幸的是,算出的阻力系数只有0.262——比实验值的一半还要小。按计算结果画出的流线如图8所示;算出的分离点位于129°的位置,虽然与实验值同处于圆柱最高点后方,但是与实验值相比要往下游一些。

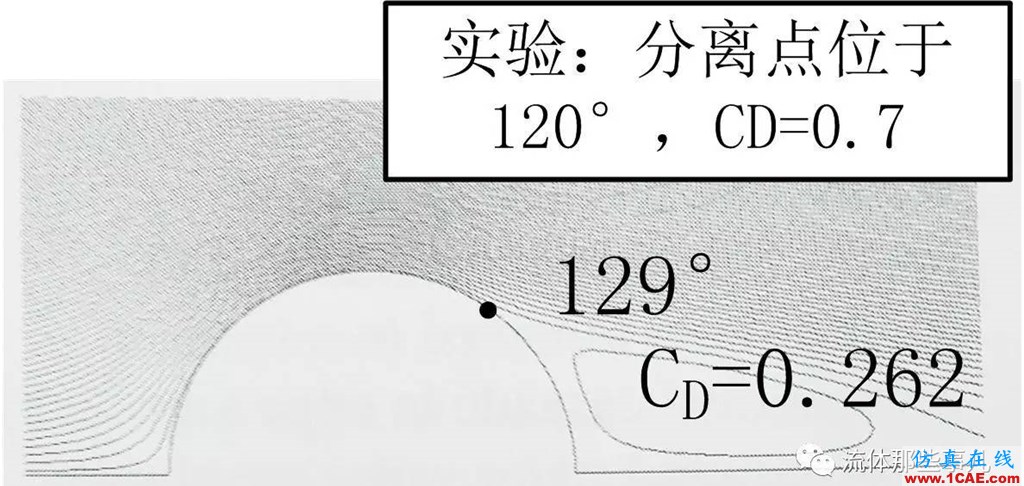
图8 Re=107的流线。数值模拟的结果。(复制自文献[2])

Re=150,104和107这三种情形分别代表了圆柱分离流动的三种最典型的流态,即“层流边界层—层流尾迹”、“层流边界层—湍流尾迹”以及“湍流边界层—湍流尾迹”。不幸的是,三种流态的数值模拟都以彻底失败告终。

实际上,对于Re=150的情形,圆柱尾迹中存在非定常的卡门涡街,附着涡交替地从圆柱的两侧脱落。而在计算模型中,根据圆柱的几何对称性天真地将计算域设为实际流动区域的一半,并在x轴上应用了对称边界条件;再者,计算过程中使用了定常的求解器;这些都是违背实际发生的物理机制的。计算结果表明,如果将计算域扩展到整个流动区域,并且使用非定常求解算法,就可以算出非定常的卡门涡街来,对算得的非定常阻力系数取时间平均之后,约为1.14,这时就落在实验值的范围(1.1~1.4)里面了。计算值接近实验值范围下限的原因可能是计算时采用了二维模型,使得任何倾斜的涡脱落或者其它三维不均匀性都被抑制了。

对于Re=104的情形,我们为了模拟湍流尾迹,使用了湍流模型进行计算。但是,实验结果表明,圆柱表面的边界层是层流的,这是计算结果不符合实际的重要原因。在我们的计算结果中,边界层的分离点位于>90°的位置;实际上只有当圆柱表面为湍流边界层时,分离点才会移动到这样的位置。总之,层流/湍流混合流动对于数值模拟来说,仍然是非常困难的问题。另外,实验表明这个雷诺数下尾迹是非定常的,而我们使用定常求解算法并在x轴使用了对称边界条件,这也是不符合实际的。

对于Re=107的情形,实际上圆柱下游存在湍流的卡门涡街,而我们使用定常求解算法并在x轴使用了对称边界条件,这是不符合实际的。

对Re=104这一类“层流边界层—湍流尾迹”的流态以及Re=107这一类“湍流边界层—湍流尾迹”的流态,要采用更细致的模拟方法才能得到合理的结果。例如,文献[3]采用了二维非定常RANS和三维DES对这两种流态进行了模拟(见注1),其结果表明,对于后一种流态,两种方法都能得到比较合理的结果;而对于前一种流态,只有三维DES才能得到合理的结果。

顺便说一句,从图2可以看出,Re=2.5×105时阻力系数突然下降。层流边界层分离点位置与湍流边界层分离点位置的截然不同,正是造成这时阻力系数突然下降的原因。当雷诺数超过此值时,边界层从层流转捩为湍流,由于湍流边界层对抗分离的能力比层流的强,所以分离点突然从<90°的位置移动到>90°的位置,使得尾迹显著变窄,压差阻力大大降低。这就是著名的圆柱绕流“阻力危机”(drag crisis)现象。所谓的危机并不是流动现象有什么很坏的影响,而是说这个现象使传统的流体力学理论受到了挑战,学术界出现了危机[4]。

从这几个例子还可以看出,要正确地模拟流动问题,必须对流动的物理机制有一定的认识;不懂物理机制而盲目地进行计算,常常会得到错误的结果。

未经许可,不得转载

参考文献

[1]庄礼贤, 尹协远, 马晖扬. 流体力学. 第二版. 中国科学技术大学出版社,2009

[2] Yunus A. Çengel, John M. Cimbala. Fluid Mechanics: fundamental and applications. McGraw-Hill, 2014

[3] ANDREI TRAVIN, MICHAEL SHUR, MICHAEL STRELETS and PHILIPPE SPALART. Detached-eddy simulations Past a Circular Cylinder. Flow, Turbulence and Combustion, 63, 1999

[4] 王洪伟. 我说理解的流体力学. 北京:国防工业出版社,2014

注1:RANS是“雷诺平均方法”(Reynolds averaged Navier-Stokes),即我们在商业软件中常用的湍流模型;DES是“脱体涡数值模拟”,即在流动附着于壁面的区域采用RANS,在其它区域自动转变为大涡模拟。

转自公众号:流体那些事儿

开放分享：优质有限元技术文章,助你自学成才