残差一定要降到1e-03以下才代表收敛吗？【转发】

2017-08-15 by:CAE仿真在线来源:互联网

太长不看版

判断收敛不仅要看残差,而且要使用monitor来监测计算结果随迭代次数的变化情况。另一种方法是使用双精度求解器:当采用单精度求解器算到残差不再下降的时候,采用双精度求解器继续计算,如果残差能继续显著下降,那就说明计算是收敛的,否则就说明计算不收敛。

总所周知FLUENT的默认收敛标准是残差降低到1e-03以下(能量方程和P-1方程除外,这两个方程的默认收敛标准是1e-06)。但是,残差降低到1e-03以下和收敛是否有必然联系呢?换句话说,残差不能降到1e-03以下,是否意味着不收敛?

先看两个例子。

例1:三维方腔突扩突缩流动

这是公众号先前的文章“为何我这个流动总是算不收敛?我要砸电脑!”中的例子。如图1所示,一个边长为2m的立方体连接着两根方形截面的管子。入口流速是1m/s,流体的密度是1kg/m3,粘性系数是10-5Pa•s。以入口流速为特征速度,入口截面的边长为特征长度,则流动雷诺数为105,所以流态是湍流流动。坐标原点位于立方体的中心,坐标轴的方向如图所示。使用FLUENT中的基于压力的求解器计算,速度和压力的耦合(Pressure-Velocity Coupling)采用SIMPLE算法,湍流模型使用k-ω SST。入口使用velocity-inlet边界条件,流速按上述条件设置。入口的湍流参数设为:湍流强度=5%,水力直径=1m。出口使用pressure-outlet边界条件,回流的湍流参数设为与入口相同。计算前的初始流场按照入口边界的数值初始化。

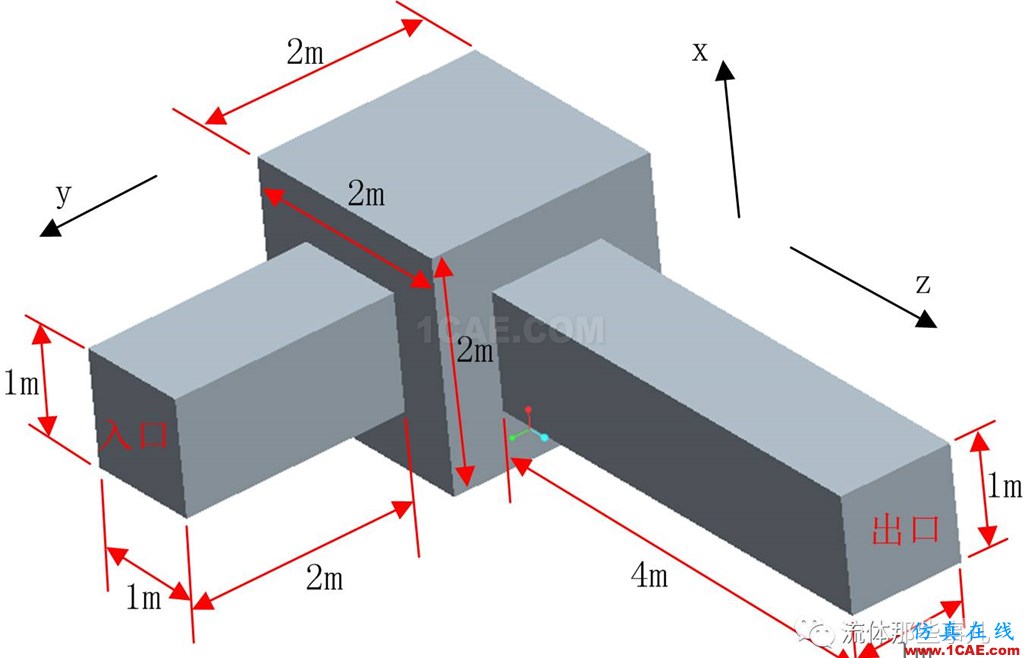
图1 例1

用定常算法(Steady)来计算,发现迭代500次之后,各方程的残差都开始振荡,在1e-02和1e-03之间徘徊,不再下降;特别是k方程和ω方程的残差,从来未曾下降到1e-03以下(图2)。

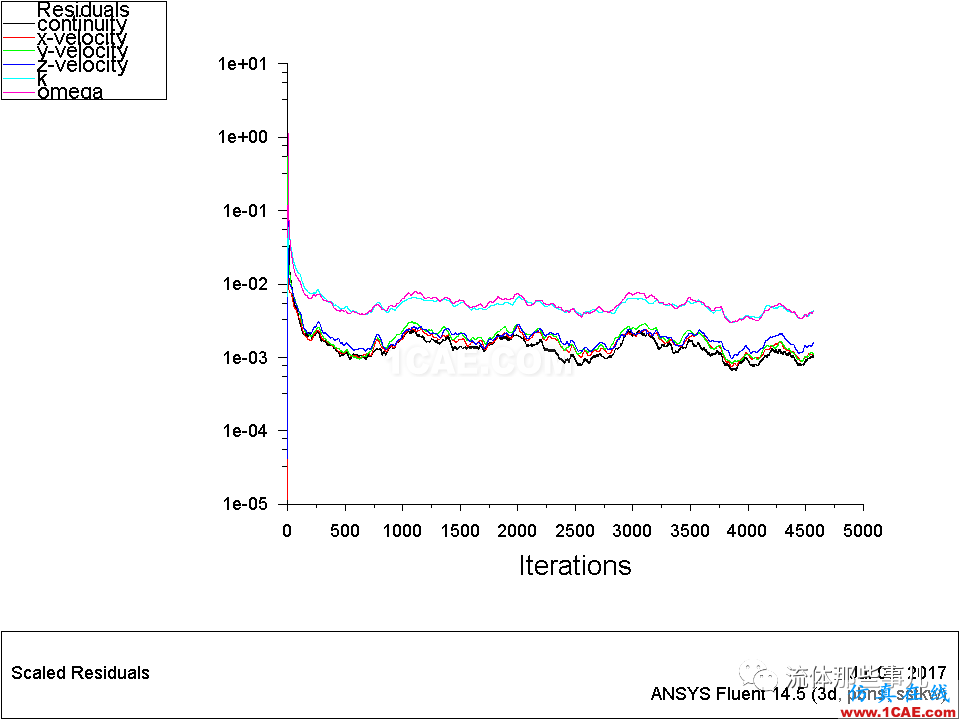
图2 例1——残差曲线

使用monitor监测点(-0.5,0.5,0.5)处的流速随迭代次数的变化情况,其曲线振荡得非常厉害(图3)。所以显然这个题没有收敛。

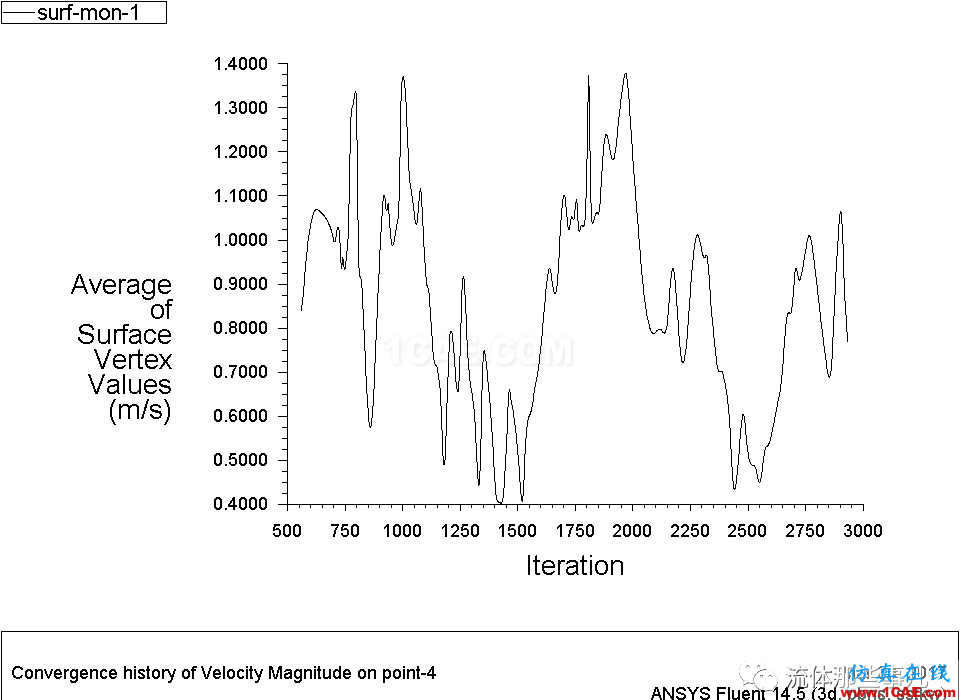
图3 例1——(-0.5,0.5,0.5)处的速度随迭代次数的变化情况

例2:圆管内的湍流流动

空气(密度=1.225kg/m3,粘性系数=1.7894×10-5Pa•s)流过一根直径为0.03m,长度为2.4m的圆管,使用二维轴对称模型计算,入口使用速度入口(velocity-inlet)条件,参数设为:流速=10m/s,湍流强度=5%,水力直径=0.03m,出口使用压力出口(pressure-outlet)条件。使用基于压力的求解器,算法为SIMPLE,湍流模型采用标准k-ε模型。计算前的初始流场按照入口边界的数值初始化。

图4 例2——管道入口附近的网格

残差曲线如图5所示。可以看出,虽然其它几个方程的残差都降到很低,但是连续方程的残差降低到2e-2左右就不再下降了。

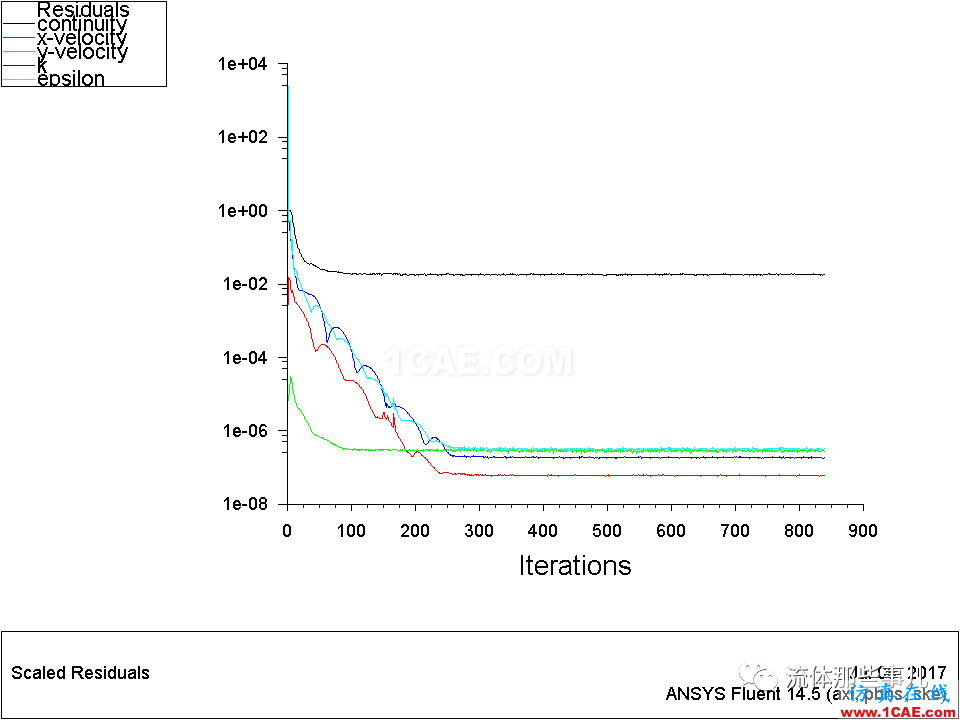
图5 例2——残差曲线

但是,如果我们使用monitor监测流场的变化情况,可以发现随着迭代次数的增加,流场并没有发生变化(图6-图9),所以这个题是收敛的。

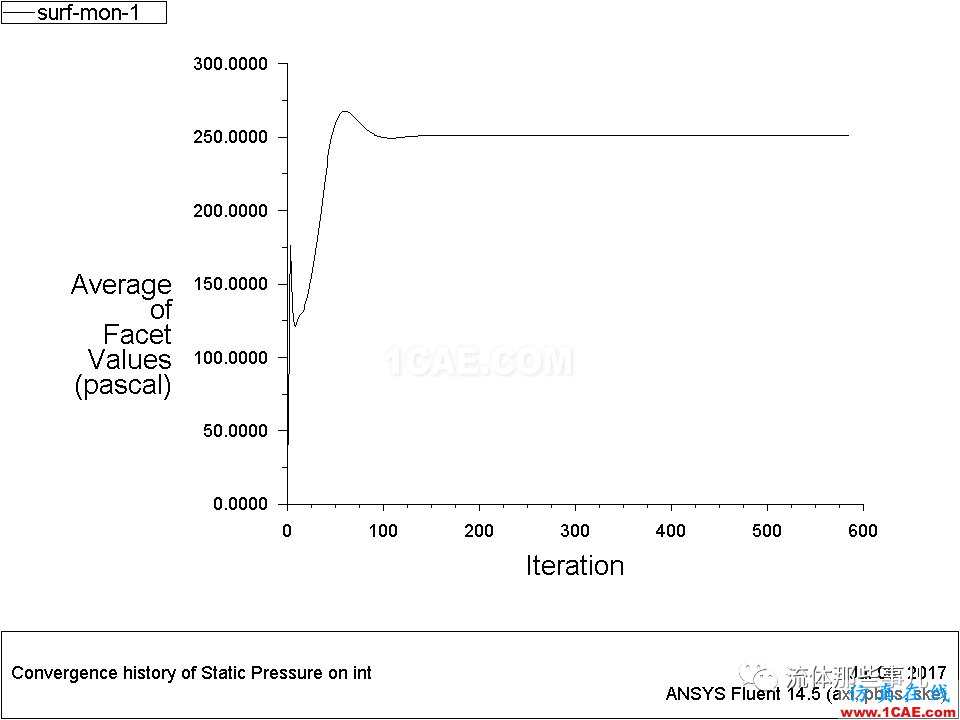
图6 例2——管道入口压力随迭代次数的变化

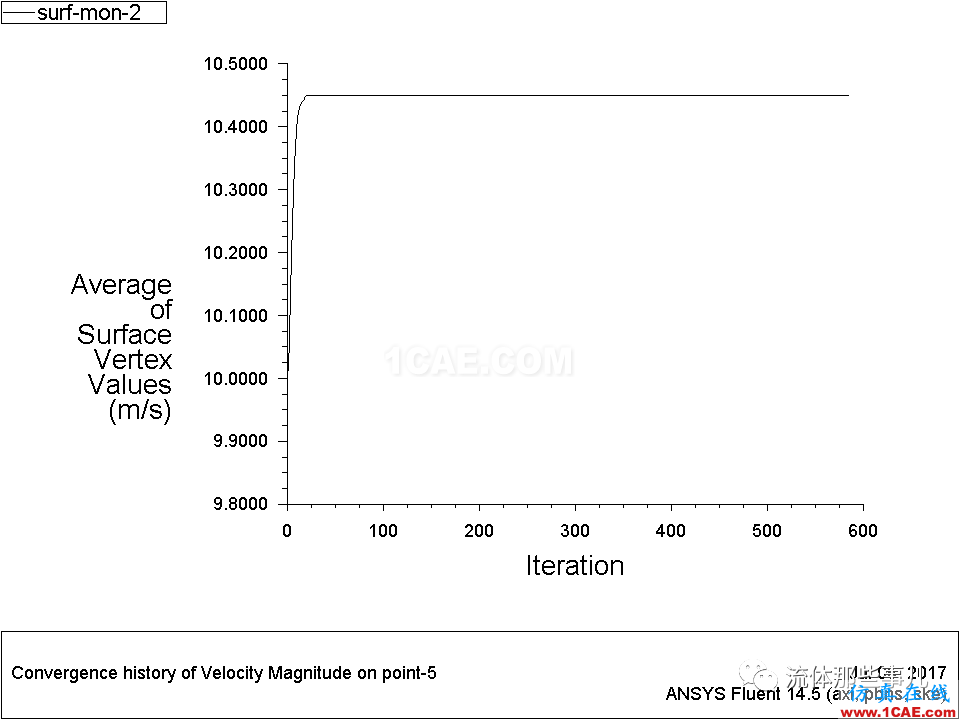
图7 例2——管道入口附近某个点的速度随迭代次数的变化

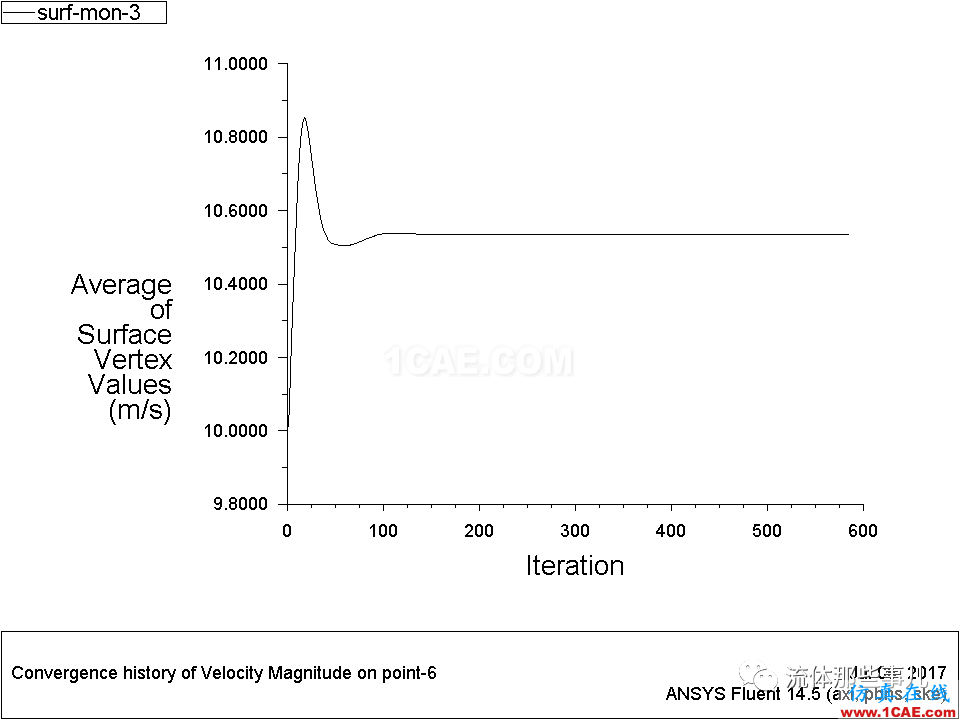
图8 例2——管道中部某个点的速度随迭代次数的变化

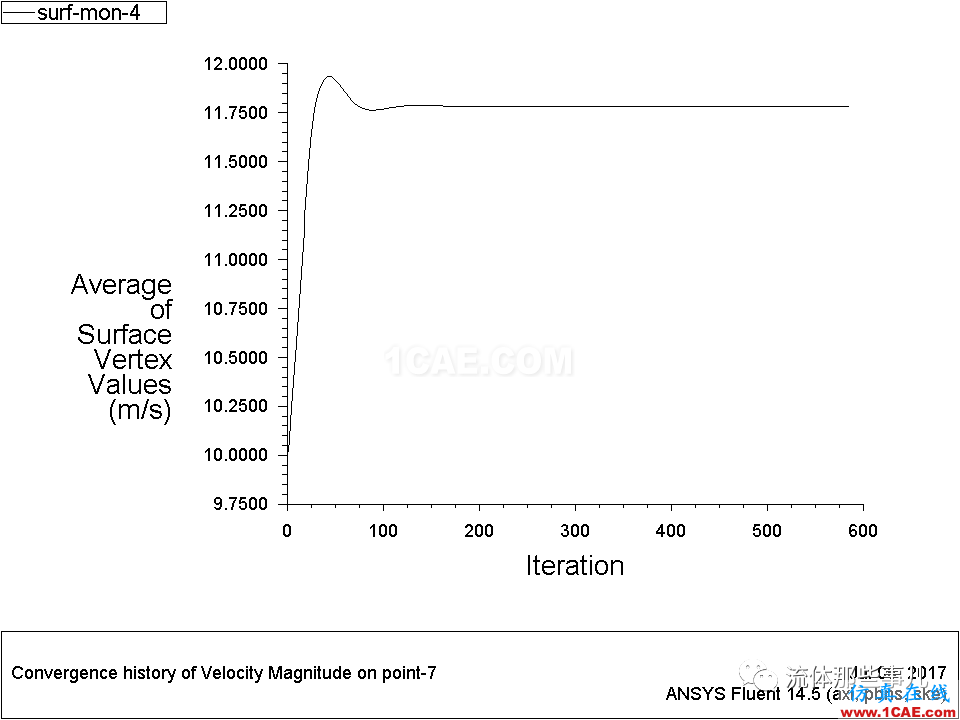
图9 例2——管道出口附近某个点的速度随迭代次数的变化

从这两个例子可以看出,并不能用残差是否能降低到1e-03以下来判断收敛。其实,在FLUENT的User’s Guide [1]中“Judging Convergence”这一节中,也指出了判断收敛不仅要看残差,而且要使用monitor来监测计算结果随迭代次数的变化情况。要弄清这个问题,需要知道FLUENT是怎样计算残差的,关于这方面的内容在FLUENT User’sGuide中“Definitionof Residuals for the Pressure-Based Solver”和“Definition of Residuals for the Density-Based Solver”中有介绍。例如,FLUENT的基于压力的求解器在计算连续方程的残差的时候,会将每次迭代的残差都除以最初5次迭代的残差,然后才显示到残差曲线图上。因此,如果用户在迭代之前设定的初始条件已经比较接近实际的流场,那么最初5次迭代的残差就会比较小,这样的话残差曲线上显示出来的数值就会比较大(这正是例2中发生的情况)。

用FLUENT计算一个题,如果已经计算到残差不再下降了,这时判断是否收敛的一种方法是采用monitor监测计算结果随迭代次数的变化情况。此外还有一种方法,那就是改用双精度(double-precision)求解器。例如,对于上面的两个例子,如果我们分别改用双精度求解器来计算,那么将得到图10、图11所示的残差曲线。可以看出,对于例1,改用双精度求解器之后,残差没有显著变化;而对于例2,改用双精度求解器之后,连续方程的残差可以降低到1e-08以下。注意,这里对每个题都采用双精度求解器从头开始计算,其实在实际的计算中,可以将单精度求解器计算的结果导入到双精度求解器中继续计算。

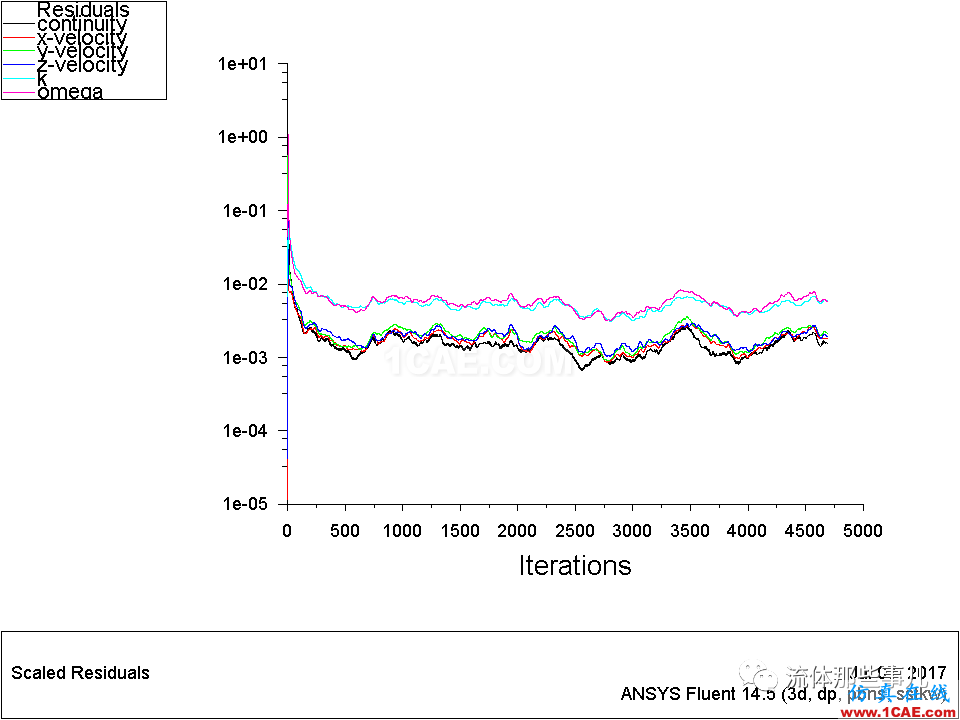
图10 例1——残差曲线。双精度求解器。

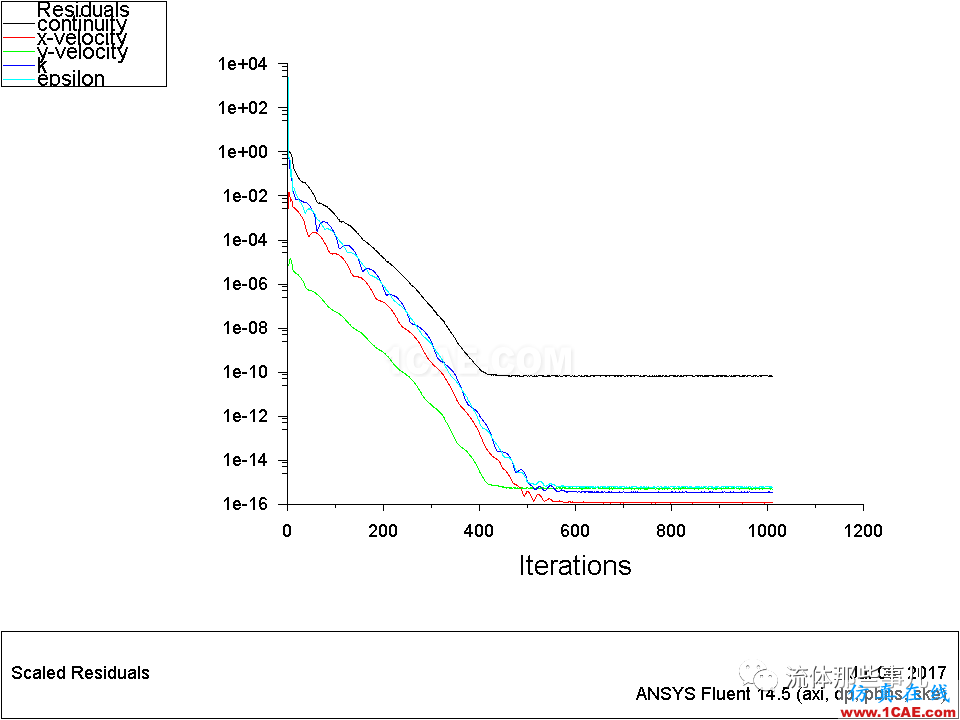
图11 例2——残差曲线。双精度求解器。

也就是说,计算一个题,当采用单精度求解器算到残差不再下降的时候,采用双精度求解器继续计算,如果残差能继续显著下降,那就说明计算是收敛的,否则就说明计算不收敛。这其中的道理其实很简单。残差不能下降的原因有两种,一种是因为计算误差已经降低到机器精度,而另一种则是因为设置不当导致计算不收敛(例如使用定常的求解器计算具有强烈的非定常分离的流动)。单精度求解器是使用单精度浮点数计算的,其机器精度大约有7位有效数字;而双精度求解器是使用双精度浮点数计算的,其机器精度大约有16位有效数字。因此,如果残差不能降低是机器精度导致的,那么改用双精度求解器之后残差可以继续显著降低。反之,如果残差不能降低是计算不收敛导致的,那么改用双精度求解器是无济于事的。

作者感谢北京航空航天大学宇航学院的研究生张少卿和冯盛;他们提供了例2的素材。另外,北航宇航学院的研究生衣然阅读了本文的初稿并提出了很好的建议。

转自公众号: 流体那些事儿叶汉玉

开放分享：优质有限元技术文章,助你自学成才