CFD最基本的数学概念:张量
2017-08-12 by:CAE仿真在线 来源:互联网
在CFD的学习中,最先接触的无非就是张量、导数以及各种积分定律了。本文简单介绍CFD中最基本的张量。
标量是一个单一的值,在任意的坐标系统中,标量都是单一的值(重复一遍)。其表示某一空间点和某一时间点具有单位的物理特性。典型的标量为流场温度、质量分数。其和流场的位置以及某一时刻均有关。标量可用于对物理量的某1个特性进行追踪。
矢量具有大小和方向,在任意的坐标系统中,矢量均具有三个分量。矢量可用于追踪物理量的2个特性,例如大小和方向。CFD中最常见的矢量即为速度矢量。在三维坐标下其具有三个速度分量。且速度的模表示速度的大小。
如果我们要追踪某个物理量的3个特性怎么办?
张量不仅可以追踪3个及3个以上特性。对于N阶张量,其具有3^N个分量。例如,零阶张量即为标量,一阶张量即为矢量。
二阶张量的典型例子即为应力以及形变率。
以应力举例,在各大教科书中我们均会发现类似下面的定义:

其即为应力张量(应力)。它是一个二阶张量,具有9个分量。对于应力张量我们可以追踪3个特性:大小、方向、作用的平面。
以下图为例:
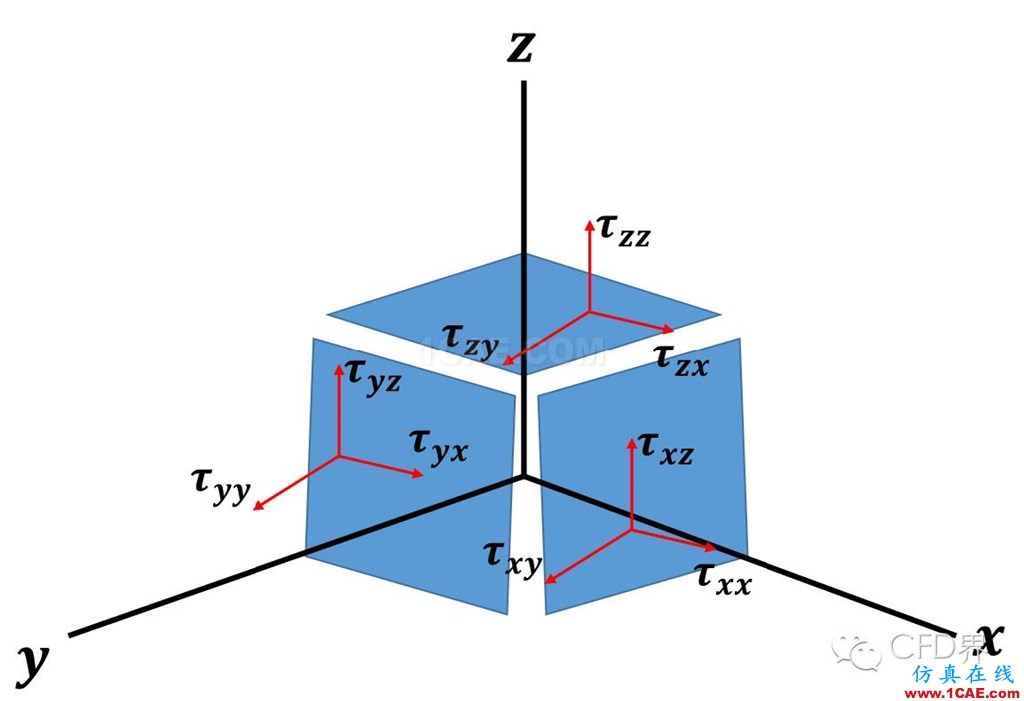
作用于这个小正方体上面的应力张量具有上述9个分量。τ_yx是一个标量。其中的下标yx具有两个含义,第一个下标y表示作用于和y坐标轴垂直的平面,第二个下标x表示作用于这个平面上的沿x方向的力。
通过应力张量的定义,对小正方体的任意的撕扯都会被表达!
1.对于某些情况下,张量是对称的,也就是τ_yx=τ_xy,τ_yz=τ_zy,τ_zx=τ_xz。在这种情况下,我们就只有6个独立分量。
2. 某些情况下,我们会发现分量为负值。这表示对小正方体向内的挤压。正值表示对小正面体向外的拉伸。
那么问题来了,CFD中的压力到底是标量还是矢量呢?
相关标签搜索:CFD最基本的数学概念:张量 Fluent培训 Fluent流体培训 Fluent软件培训 fluent技术教程 fluent在线视频教程 fluent资料下载 fluent分析理论 fluent化学反应 fluent软件下载 UDF编程代做 Fluent、CFX流体分析 HFSS电磁分析






