CFD中的高阶精度是不是扯淡
2017-08-12 by:CAE仿真在线 来源:互联网
(本文对英文原文适当概括)
先看高等数学对面积分的定义...,如图:
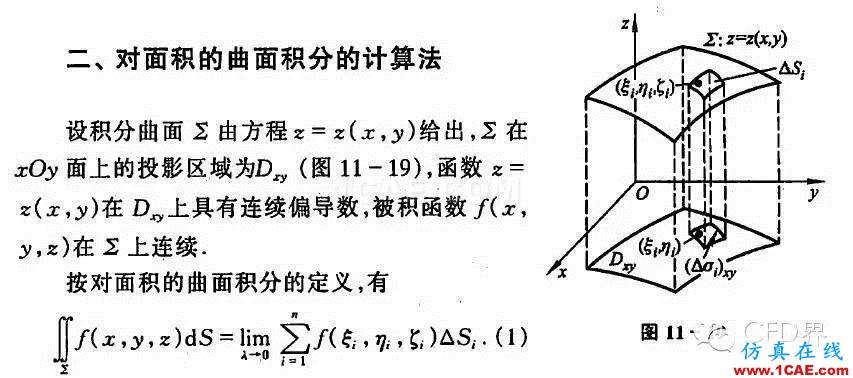
(不要看文字...不要被各种专业名词绕进去,其实很好理解)

他的意思就是说,对f在面S上的面积分等于n个面微元的大小乘以对应的n个f的值之和 (最后的公式)。
以上来自高等数学同济版下册
然后看CFD中的面积分(下面的公式和上面的一个道理):
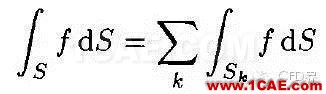
为了准确的计算上述方程表示的面积分,需要知道每个面上的f值。当然我们不知道每个面的f值,因此我们引入了各种插值方法。这涉及到2种插值:
-
面积分的积分点可以从1到n,即k=1,2,3,...,n;
-
面上的f值需要从体心值插值而来;
先看第一条:最简单的当然是中点(midpoint)规则。它认为积分等于f在面心的值和面积大小的乘积(即高等数学的公式中i=1,面微元就是整个面,f的值为f的面心值)。中点规则为二阶精度的。
当然我们可以达到更高的精度,比如如果采用辛普森(Simpson)规则,我们的面积分这样计算:
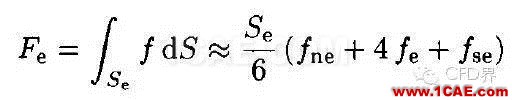
就是说,k=4。我们使用了4个点来计算这个面积分(中点规则使用了1个点)。
再看第二条:从体心插值到面心大家都很熟悉,就是迎风、中心、QUICK等格式。具有不同的精度。
如果我们针对第一条使用了中点规则达到了二阶精度,那么我们对面心f的值进行插值的时候也要至少保留二阶精度。
如果我们针对第一条使用了辛普森规则达到了四阶精度,那么我们对面心f的值进行插值的时候也要至少保留四阶精度(比如Cubic格式)。
不难理解,如果在从“体心插值到面心”的这个过程调用了高阶精度格式,比如调用了三阶精度的QUICK格式,那么我们在第一条就至少调用三阶精度的面积分规则。举例:
二阶精度的中点规则+三阶精度的QUICK格式=二阶精度。
四阶精度的辛普森规则+三阶精度的QUICK格式=三阶精度。
因此,只有在面积分调用高阶精度的时候,插值的高阶精度才有意义。
然而CFD中通常使用二阶精度的中点规则,这是不是就意味着高阶精度就是鬼扯...

下面我们请出Henry!看看他怎么说:
OpenFOAM使用的就是中点规则,因此不管你怎么插值,规则网格上的体积分都是二阶精度。但是,对流项还是使用高阶格式好一点。当然了你可以使用高阶精度的面积分,但我觉得没必要。或者,可以使用FDM,如果守恒不是很重要的话。

Computational Methods for Fluid dynamics 3rd Edition. Chapter 4.
相关标签搜索:CFD中的高阶精度是不是扯淡 Fluent培训 Fluent流体培训 Fluent软件培训 fluent技术教程 fluent在线视频教程 fluent资料下载 fluent分析理论 fluent化学反应 fluent软件下载 UDF编程代做 Fluent、CFX流体分析 HFSS电磁分析






