三环减速器建模动态特性有限元分析计算
2016-03-12 by:CAE仿真在线 来源:互联网
引言
对三环减速器振动系统进行振动与噪声的分析与研究,首先必须建立其数学模型,数学模型有理论建模和试验建模两类。所谓的理论建模是指由结构、机械的设计图纸出发,作出必要的假定与简化,根据力学原理建模;而试验建模是对振动系统进行激振,通过没量获得系统的输入、输出数据,再经过对它们的分析、处理而建立 的模型。这两类方法各有其特点,可分别适用于自己特点的情况。在此,我们仅讨论对三环减速器振动系统进行理论建模,并在SUN工作站上用I-DEAS软件 的有限元模块及实体建模模块对SHQ40建模并计算,而试验建模我们将在第六章中讨论。
3-2 描述振动系统的方法
振动系统有确定性和随机系统两大类,在这里,我们主要讨论确定性振动系统。确定性振动系统通常分为分布参数振动系统和离散振动两大类,不同的振动系统存在其相应的描述方法。
3-2.1 分布能数振动系统
具有分布质量、弹性和阻尼的系统,称为分布参数或连续参数系统。在域D的每一点都应满足如下的运动微分方程。
![]()
式中:U(p,t)——任意点p的位移,它应满足的边界条件是:
B,[u(p,t)]=0,(i=0,1,2……,p);
L—一个线性的2P阶齐次数微分算子,它描述了系统的刚度分布;
C—一个类似于算子L的2P阶线性齐次数分算子,它描述了系统的阻尼分布;
M—线性齐次微分算子,它描述了系统的质量分布;
f(p,t)——分布激振力;
![]()
A1,A2……——坐标x,y,z的函数;
x,y,z——p点的坐标,即p(x,y,z);
B1——线性齐次微分算子;
由式(3.1)可知,分布参数系统的运动是以偏微分方程来描述的,这类运动方程中所包含的参数,通常是空间变量的连续函数。分布参数系统具有无限多个自由度。所以,与一个分布参数系统相对应的特征解是由可数的然而是无限多个特征值和特征向量组成。
为了获得可靠的、精确的分布参系统的数学模型,就需精确地确定运动方程中的各个参数。为此,利用如上述的试验建模方法——振动参数识别技术是一个有效的方 法。通常,分布参数振动系统的参数识别方法有:(1)将分布参数系统离散化,获得离散系统的模型,然后识别离散模型中的参数或与它相应的特征解;(2)直 接以从布参数系统的响应识别分布参数系统运动微分方程中的各参数;(3)首先识别与实际分布参数系统相应的离散模型的特征解,然后,利用识别的特征解来识 别方程中的各个参数。
一个分布参数系统有无限多个的特征值与特征的向量。但是,人们不可能识别完全的特征解,通常是识别与该系统相应的低阶特征值和特征向量。此外,目前的技术水平还不能满足分布式测量的要求,因此,其识别工作还得借助于离散式测量来完成。
3-2.2 离散振动系统
分布参数系统是一个非常复杂的系统,它给振动分析和振动参数识别带来了很大困难,主要表现在:(1)系统的惯性、弹性、阻尼、激励力和运动都依赖于空间坐标,因而导致数学上较难处理的偏微分方程及复杂的边界条件。因此,一般情况下,除了少量的简单结构外,很难获得严格的封闭形式的解;(2)不可能获得分布 的响应测量及无限多个特征解。因而,实际作振动分析、振动参数识别时,通常将无限多个自由度的分布参数系统离散为有限自由度的离散振动系统。把分布参数系 统离散化一般有以下几种方法:
一、集中质量法
把结构的质量分别集中在若干点而形成有限个质点的集中参数系统。质量元件、弹性元件和阻尼元件分别只有惯性、弹性和阻尼特性;
二、广义坐标法
把结构的变形分解为一系列具有固定形式的函数,而以广义坐标表示结构的变形。这种方法,虽然理论上需要考虑无限多项,但实际上只要考虑有限几项即可获得具有足够精度的计算结果。如瑞利—里兹法、模态坐标法等。
三、有限元法
可以哈密顿原理导出的拉格朗日方程,导出离散振动系统的一般运动微分方程式:
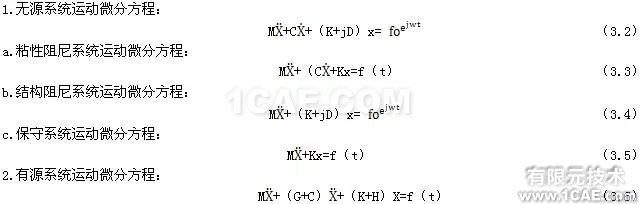
上式中:M——质量矩阵,正定矩阵;
C——粘性阻尼矩阵,实对称正定式或半正定短阵;
D——结构阻尼矩阵,实对称正定式或半正定短阵;
K——刚度矩阵,实对称正定式或半定矩阵;
G=-GT——陀螺矩阵,反对称矩阵;
H=-HT——循环矩阵,反对称矩阵;
f(t)——激励力矩阵;
![]()
对于无源系统,当系统作任一运动时,D就再出现,当振动系统中存在传递功率的曲柄、轴、滑动与装置时,常形成陀螺效应和循环力,这时系统就成为有源系统。
3-2.3 离散振动系统实模态坐标描述
仅讨论无阻尼离散振动系统,无阻尼自由振动系统运动微分方程由式(3.5)确定为:

求解上式得特征值,即得离散振动系统的固有频率ω,然后将ω代入式(3.8)就可能解出固有振型矩阵 ф,则由ω、ф就构成了振动系统固有模态参数。由于各阶固有振型ф,具有加权正交性质,且又是线性独立的,那么就可由固有振型ф构成一个n维空间的完备的 正交基,作为一个新坐标系,称之为固有模态坐标系。于是对应于原物理坐标系的任一向量x(t),在n维空间中,可表示n阶固有振型的线性组合,即:
![]()
式中q——模态位移向量;
将式(3.10)代入式(3.5),再以φT前乘可得:
![]()
由上式可知:在实模态坐标系里,用物理坐标系描述的运动微分方程,变成n个独立互不耦合的动运微分方程。解式(3.11)可确定q,再由式(3.10)可确定物理坐标系下的响应X(t)。式(3.10)是物理坐标系和固有模态和固有模态坐标系之间相互转换的重要关系式。
§3-3 三环减速器振动系统的数学模型
根据三环减速器的结构原理,如图2-3(a)(b)和图2-4(a)(b)所示。我们将其振动系统数学模型建立如图3-0所示。
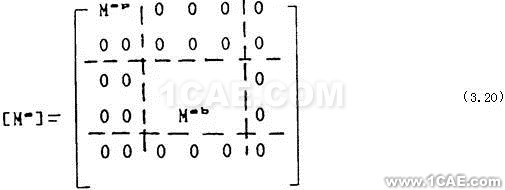
图3-0 三环减速器振动系统教学模型
该模型由Ⅰ、Ⅱ两个子模型组成,其中Ⅰ子模型为传动链及其附件部分,Ⅱ子模型为箱体部分。Ⅰ、Ⅱ子模型间通过轴与轴承在a、b、c、d、e、f处紧密联接而构成三环减速器振动系统数学模型。
Ⅰ、Ⅱ子模型振动系统都是由分布参数振动系统,它们实际的数学模型应曲式(3.1)来描述,但在实际作振动分析、振动参数识别时,我们将Ⅰ、Ⅱ两个子模型 都作为离散振动系统来考虑,即由式(3.2)~(3.6)来确定其相应的数学模型。
一、Ⅰ子模型振动系统数学模型
由图2-2、图2-3(a)(b)及图3-0分析知,Ⅰ子模型主要为传动链及其附件,用于传递系统的运动和动力,分析其传动结构及原理,根据式(3.2)可得Ⅰ子模型的数学模型为:
![]()

Krθ——轴、环板弹性矩;
Krθθ——各联接处弹性矩;
Kgθθ——轮齿弹性矩;
Mgg——由齿形识别差引起的力矩;
Mgf——由齿面摩擦力引起的力矩;
Mrf——各联接处的摩擦力矩;
Mb——轴承非线性刚度引起的弹性矩;
MD——传动链中轴承阻尼力;
Mx——双曲柄机构额外冲击力矩;
M——外界激励力矩;
式中Mx的成因及其对Ⅰ子模造成的影响在第二章中已有论述。
二、Ⅱ子模型振动系统数学模型
由图2-2、图2-3(a)(b)及其图3-0分析知,Ⅱ子模型为箱体结构,显然Ⅱ子模型为无源振动系统,故可根据式(3.2)、(3.3)、(3.4)、(3.5)知其数学模型为

Kx——弹性力;
F(t)——外界激励力;
三、Ⅰ、Ⅱ子模型间关系
由图3-0所知,Ⅰ、Ⅱ子模型间在a、b、c、d、e、f处紧密相连,Ⅱ的外界激励力F(t)就是由Ⅰ通过a、b、c、d、e、f处作用于Ⅱ子模型而引起 的,通过对Ⅰ子模型进行分析可计算出Ⅰ对Ⅱ的激励力F(t),将F(t)代入Ⅱ的式(3.13),就可对Ⅱ子模型进行动态特性的分析计算。
F(t)主要同Mgg、Mgr、Mrg、Mrf、Mb、MD、Mx等组成,在本研究中,我们用试验的方法来确定F(t)的大小,见第四章。
从上述分析中可知,在三环减速器振动系统中,Ⅰ子模型是产生振动和噪声的根源地,Ⅱ子模型是振动与噪声传播体。在第二章中,我们已分析了Ⅰ子模型产生振动、噪声激励的原因,在本章中我们仅讨论Ⅱ子模型受激后的振动与噪声问题。
§3-4 三环减速器箱体理论建模和有限元(FEM)法分析
§3-4.1 壳体结构
所谓的壳体结构定义为在两个具有小间距的以曲双面之间的密闭式体。这两个曲面间的距离,就是壳体结构的厚度。如果厚度与结合面的外廓尺寸相比很小的话,那 么这个壳体就定义为薄壳结构;反之则为厚壳结构。壳体结构实质上是一种可由薄板转化而来的结构,其法是非曲是一开始就将中面做成单曲(或双曲)的曲。虽然 关于应力和应变沿横向分布的假设仍然成立,壳体承受外载荷的方法却与平板完全不同。平行壳体中面作用的应力合力现在产生曲面法方向的分量,并且这一应力合 力平衡了载荷的大部分。这就是壳体作为承载结构比较经 济而且受到广泛应用的原因。
广泛应用于工业中的齿轮传动装置的箱体结构,根据使用场合的不同,有的就可以作为壳体结构来处理,并且一般箱体的材料都是均质、名向同性和完全弹性的(在一定范围内),这样就更利于对箱体的特性理行分析计算。
本研究中的SHQ40型三环减速器如图6-4(a)(b)及图3-1所示,其箱体的长宽高尺寸分别为708mm,147mm和385mm,厚度仅为8mm,所以在这里我们将其作为薄壳结构来进行研究,以分析其动态特性。
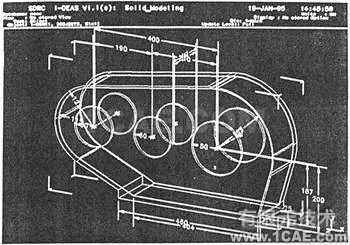
图3-1 SHQ40箱体尺寸图
§3-4.2 三环减速器箱体结构有限元(FEM)法理论分析
对于三环减速器箱体,即Ⅱ子模型振动系统,它实质上是一个连续的振动系统,我们必须将其离散化作为离散振动系统来进行分析计算,这我们已在第二节中详细讨 论过了。在这里,我们用有限法(FEM)对箱体离散化壳体结振动系统进行理论上的分析和计算。
一、三环减速器箱体结构有限元法(FEM)理论分析
所谓的有限元法,顾名思义,就是假设箱体薄壳体结构是由一系列薄壳小元素组成,称它们为有限元素。这些小元素通过它们交界上的一些点连接起来,这些点称为 节点。元素间的相互连接必须满足交界面上节点拉移协调条件和节点的力平衡条件。元素中任一点的位移用节点位移表示,取节位移为广义坐标。用弹性位能和动能 公式建立元素的质量矩阵、刚度矩阵。在元素质量矩阵、刚度矩阵的基础上,根据交界面上节点位移协调条件和节点的平衡条件组装成系统的总质量矩阵和总刚度矩 阵。于是,离散振动系统的弹性性质可用总刚度及矩阵来描述,惯性性质可用总质量矩阵来描述,阻尼性质可用阻尼矩阵来描述。由此,可以计算出振动系统的固有 模态参数。
对箱体薄壳体结构进行有限元离散化处理时,有曲壳元和平壳元两大类。显然,用曲壳元离散箱体薄壳体结构更接近于实际情况,但当采用曲壳元时,根据所引入的 近似的不同就会导出许多不相同的公式系统,给分析计算带来了一定的困难,且用曲壳元来计算所获成功的例子很少,而用平面壳元来对箱体薄壳体结构进行离散化 处理时,只要有限元素尺寸大小合适,采用平面壳元近似所带来的误差与对连续系统离散化处理所带来的误差是同一阶的,且分析计算大大的简化了。综上所述,我 们采用平面壳元对Ⅱ子模型进行有限元离散化处理。
平面壳元一般产生弯曲和面内两种变形,根据二者不干涉的假定,我们在分析时可分别处理之。
平面壳元根据节点数的不同可分为线性(一次)、二次或更高阶次的元;根据形状的不同可分为三角形、矩阵或别的形状等。在这里,我们根据三环减速器箱体结构 和特点及我们实际研究的需要,用线性薄壳矩形元对三环减速器箱体结构进行有限元离散化处理并分析,如图3-2示和图3-9示。
二、三环减速器箱体有限元法推导
对三环减速器箱体进行有限元理论分析计算的具体步骤简述如下:
1、用线薄壳矩形元把箱体离散化。
2、形成线薄壳矩形元的刚度矩阵[Kω]和5质量矩阵[Mω]
线性薄壳矩形元,它同时承受“面内”力和弯矩作用,如图3-2所(a)、(b)所示。
首先考虑面内力作用下的情况,如图3-2(a)示,应变状态由各节点的位移u,v唯一地描述,节点力fωp为:

类似地,当考虑弯矩作用下的情况时,如图3-2(b)所示。应变状态曲Z方向的节点位移ω及两个转角θx、θy唯一地描述,产生如下类型的刚度矩阵:

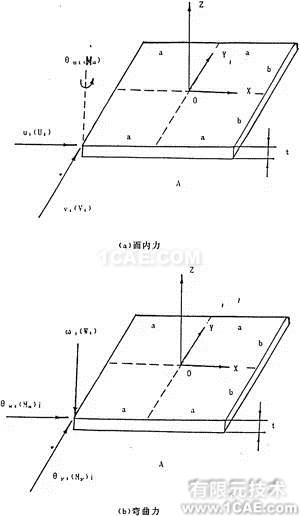
图3-2 线性薄壳距形元
在组合上述两个刚度短阵之前,有两点应注意,根据线性薄壳元互不干涉的假定,首先,对于面内力所规定的位移不影响弯曲变形,且反之亦然;其次,在两种模式中,转角θz都不作为参数进入变形定义式。但现在我们再考虑这一转角,并令一假想力矩Mr与其对应,则节点的位移为:

式中刚度矩阵为:

同样方法可以导出质量矩阵为:

以上清式的分析,全部是在局部坐标系(o,x,y,z)中进行的,再将它们合成整个系统的元素之前,应变换到总体坐标系(o′,x′,y′,z′)中,设局部坐标系与总体坐标系间的转换矩阵为[L],则在总体坐标系中单元的刚度矩阵Kω′和质量矩Mω′。
[Kω′]=[L]T[Kω][L] (3.21)
[Mω′]=[L]T[Mω][L]
这样我们就可以得到单元在总体坐系中运动的方程式为:
[Mω′]x′ω+[Kω′]xω=0 (3.22)
然后进一步可以构构造出Ⅱ子模型系统的运动方程式:
[M]x+[K]x=0?(3.23)
式(3.23)与第三节中建立的Ⅱ子模型的数学模型式(3.13)是一样的,建立了系统的运动方程式后,若再对Ⅱ子模型加上边界约束条件即或进行有限元的计算了。
对式(3.22)我们用式(3.10)将其转化到实模态坐标系里,就可求解Ⅱ子模型振动系统的固有模态参数。
相关标签搜索:三环减速器建模动态特性有限元分析计算 三环减速器建模动态特性有限元分析计算 有限元技术 Ansys有限元培训 Ansys workbench培训 ansys视频教程 ansys workbench教程 ansys APDL经典教程 ansys资料下载 ansys技术咨询 ansys基础知识 ansys代做 Fluent、CFX流体分析






