ANSYS对压路机十字铰接轴的疲劳分析

2016-10-25 by:CAE仿真在线来源:互联网

概述:

疲劳是产品/零件失效最常见的方式之一。疲劳的种类很多,常见的有机械疲劳、腐蚀疲劳、高温疲劳、热疲劳和微动疲劳等,其中机械疲劳包括应力疲劳、应变疲劳和接触疲劳3种方式。引起疲劳失效的机理和因素比较复杂,因此,必须遵循客观规律和按照严格的分析程序进行失效分析和疲劳预测。

本文以某公司22吨单钢轮振动压路机十字铰接轴为切入点,对其进行结构静力学和结构疲劳仿真分析。十字铰接轴是铰接式压路机的重要机构,是前、后车架的连接件,其结构的可靠性直接影响到压路机的使用。图1为该铰接轴的三维模型,其特点是结构类似于“十”字,在“十”字的四个顶点上安装轴承(定义点1为上铰接点,点2为下铰接点,点3为后铰接点,点4为前铰接点,)分别与前、后车架连接。点5为左转向油缸作用力点,点6为右转向油缸作用力点。

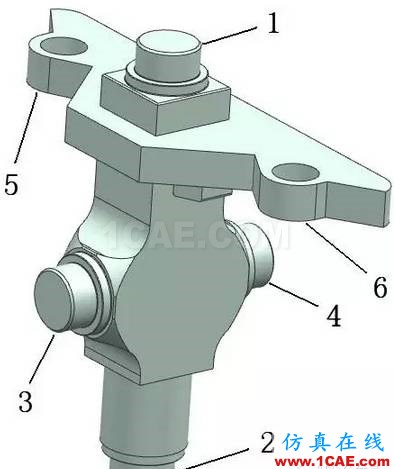
图1 十字铰接轴三维模型

首先计算该结构线性静力学中的Von Mises应力和应变值,判断结构在各种工况下是处于弹性应变阶段还是处于塑性应变阶段,这样下一步可以合理选取相应的疲劳寿命准则。

然后按照定义的疲劳寿命准则,计算以下条件的疲劳寿命:假设该模型受到1.5倍名义应力值载荷,作用周期10 000次循环,计算结构的疲劳寿命,分别按照强度安全因子、疲劳安全因子和疲劳寿命等评价指标进行查看。

2结构静力学仿真分析

2.1 创建有限元模型

在Solid-edge st3中建立三维模型,将其导入UG中。该模型为焊接件,由于在有限元模型中不允许出现细小间隙,因此,必须把该焊接件当做一个整体零件来建模,模型中省略了焊缝,一般认为质量良好的焊缝能够减小应力集中。

(1)材料选择。十字铰接轴的材料为Q345A,查阅机械手册得到该材料的屈服强度为345 MPa,极限强度为620 MPa,在UG软件的材料库中选择“STEEL”。

(2)网格划分。将建立好的三维模型进入“高级仿真”应用模块,选择“3D四面体单元网格”,单元属性类型选择“CTETRA(10)”,单元大小为20 mm,在预计会出现应力集中的边线减小相应的单元大小。图2是整体网格划分效果,划分完成后单元总数是21 116个,节点总数是34 689个。

图2 模型网格划分效果

2.2 创建仿真模型

十字铰接轴是前、后车架的连接件,是压路机工作时的重要传力部件。按照压路机行驶状态分为直线前进后退、行驶转向、原地转向等三种典型工况。经研究,压路机直线行驶时模型受力很小,只有十几MPa,而转向时,模型受力较大。

(1)行驶转向工况。

在该工况下图1中的点5和点6受到转向力作用,假设压路机右转(以下转向方向相同),点5受到一个沿着转向油缸的轴向推力,点6受到一个沿着转向油缸的轴向拉力,点1和点2主要受到后车架的径向推力,点4受到前车架的轴向阻力和与转向方向相反的阻力矩。

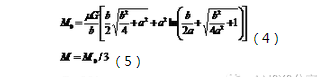
M0——原地转向阻力矩,N·m;

M——行驶的转向阻力矩,N·m;

G——前轮荷重,N;

b——钢轮宽度,mm;

a——压路机铰接中心到钢轮轴线之间的水平距离,mm;

F——点5或点6受到的转向油缸力,N;

r——转向油缸对铰接中心的力臂,mm。

这里G取110 kN,b取2 150 mm,a取1 505 mm,μ为0.31[5]。计算出原地转向阻力矩M0=55 399.62 N·m,行驶转向阻力矩M=18 466.54 N·m。

当转向角为0°时,rmax=250.37 mm,代入公式(6)得F=73.757 kN,该型号压路机采用双油缸转向,点5和点6的转向力均为0.5F,即F5=F6=36.878 5 kN。当转向到35°时,r5=202.38 mm,r6=210.45 mm,计算出F5=45.623 kN,F6=43.874 kN。为了便于计算,在作静力仿真时将点5和点6受到的力分解,一是沿点3、点4轴线方向,一是垂直于该轴方向。图3、图4分别为模型在0°转角和35°转角时的约束和载荷。图5、图6分别为该工况下整机在0°、35°转角时模型的应力分析云图。

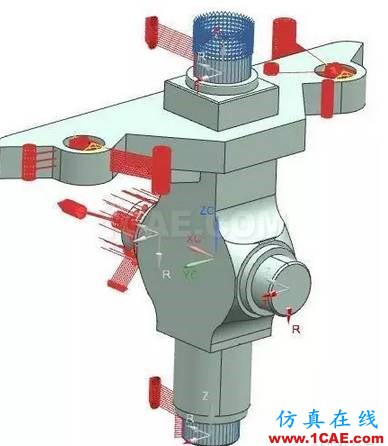
图3 0°转角时约束和载荷

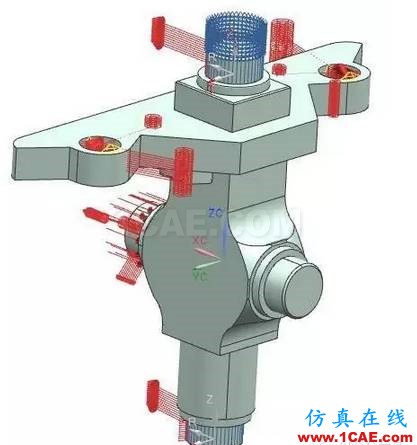
图4 35°转角时约束和载荷

图5 0°转角应力分析云图

图6 35°转角应力分析云图

从图中可以看出最大应力值发生在0°转角处,即整机开始转向时,值为157.3 MPa。但从图5和图6的云图分析,从0°到35°转向过程中,其应力值变化其实并不大,可以说在转向过程中,模型受到的应力基本是恒定的。

(2)原地转向工况。

原地转向时,后车架对点1、点2无作用力,点4也不受钢轮的轴向摩擦阻力,因此该十字铰接轴上只有点5、点6受转向油缸载荷力,点4受转向阻力矩。经解算,最大应力值为发生在35°转角处,即整机处于最大转角时,值为416.25 MPa。

2.3 仿真结果分析

模型的屈服强度σS=345 MPa,一般取安全系数nS=1.8,则许用应力为[σ]=σS/nS,即192MPa。

分析以上两种工况,在行驶转向过程,压路机受到的阻力较小,模型上的应力值未超出材料的屈服强度,但已接近材料的许用应力,此时模型处于弹性变形阶段。而原地转向需要克服更大的阻力,模型受到的载荷更大,显然某些区域应力值已经超出许用应力值,甚至一些应力比较集中的区域,其值超出了屈服强度,处于塑性变形阶段。

对于弹性变形阶段,我们可以对其进行下一步的疲劳分析。而对于塑性变形阶段,其往往代表短疲劳寿命,进行疲劳分析意义不大。

在静力计算结果中,还包括最大切应力、最大切应变、最大主应力、最大主应变等名义值,限于篇幅原因,未能在文章中体现,但在后续疲劳分析时根据不同的寿命准则,UG软件自动选取相应的值参与计算。

3 结构疲劳仿真分析

UG疲劳计算必须有材料的疲劳属性参数作为基础,因此还需添加材料的疲劳强度系数、疲劳强度指数、疲劳韧性系数和疲劳韧性指数,根据参考资料,其值分别为947.1MPa、-0.094 3、0.464 4、-0.539 5[6]。

处于工况3下的模型,在UG软件中创建疲劳解算方案中强度应力准则选取“极限应力”,设计寿命准则选取“无限寿命”,疲劳寿命准则选取“Smith Watson Topper”。疲劳载荷采用1.5倍名义应力值载荷,作用周期10 000次循环,比例函数为全周期。解算后依次展开【疲劳寿命】、【疲劳安全因子】和【强度安全因子】3个节点。

(1)点击【强度安全因子】节点,如图7所示强度安全因子云图。该图中所有单元上的SSF值均大于1,说明在该工况下模型的强度是足够的。

图7 强度安全因子云图

(2)点击【疲劳安全因子】节点,如图8所示疲劳安全因子云图。图中显示转向油缸连接板与轴焊接部位以下区域单元,FSF值均接近于0,说明该区域会最先产生裂纹和破坏,该结果与实际情况相一致。

图8 疲劳安全因子云图

(3)点击【疲劳寿命】节点,如图9所示疲劳寿命云图。图中显示转向油缸连接板与轴焊接部位以下区域单元寿命值最短,也意味着该区域容易遭受破坏。

图17 疲劳寿命图

最薄弱的节点所能经受的循环次数为31次,节点编号为79846。将此疲劳寿命云图与静力学应力分析云图对比,我们可以发现模型上疲劳寿命的分布与S-N曲线理论是符合的,疲劳寿命最低的部位就是受应力较大的地方。

特别需要说明的是,通过有限元法来计算零件的疲劳性能,主要用来预测零件结构中强度不安全的区域,或者预判零件是否存在疲劳破坏的隐患,而实际中的零件由于材料的非线性、不均匀性或者存在其它的组织缺陷,要想准确判断它的疲劳寿命,还需要进一步通过试验来验证。

4 结论

本文在UG软件中建立22吨单钢轮振动压路机十字铰接轴的有限元模型,并对其进行静态结构分析和疲劳耐久性分析,得到了该结构所受的应力应变状况以及疲劳性能。本文所使用的方法对于其它产品结构零部件的有限元分析具有重要的借鉴意义。在设计的初步阶段,预估出产品的性能,从而根据要求进一步修改,并且能为以后的实际实验提供很多有价值的参考,从而节约大量的时间及经费,这是非常具有工程应用价值的。

开放分享：优质有限元技术文章,助你自学成才