基于ANSYS经典界面的偏心圆盘启动的转子动力学分析-1(瞬态动力学分析)
2016-11-01 by:CAE仿真在线 来源:互联网
【问题描述】
一个转子如下图所示。
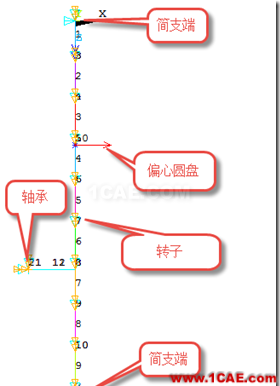
该转子两端简支,在距离下端三分之一处有一个轴承支撑;而在距离上端三分之一处有一个刚性圆盘,该圆盘存在一个偏心质量。
现在该转轴从静止开始转动,经过4秒转速达到5000RPM。要求对该转子的启动过程进行仿真,考察偏心圆盘所在处的轴位移和弯曲应力随时间变化的过程。
《注》该算例来自于ANSYS APDL转子动力学部分的帮助实例。
由于该问题涉及到一个关键技术,如果不先解决这个关键技术,则读者不容易看懂后面的程序。因此本篇博文先解决这个关键技术,下篇博文再说明求解过程。
【关键技术分析】
相对于一般的瞬态动力学分析而言,该问题除了需要考虑科里奥利效应以外,还有一个重要问题: 如何施加由于偏心质量而导致的力?
这是什么意思呢?
在刚启动时,偏心质量的位置随时在改变,从而惯性力的大小和方向时刻在改变。所以,如何施加这个随时间而改变的力呢?
需要采用数组的方式。
即首先把该力的两个分量存储到两个数组中,然后使用
f,5,fx,%fxTab%
的形式来施加这个变化的力。
上述命令的含义是,请在5号节点上施加一个X方向的集中力,该力的大小随时间而改变,其值记录在数组fxTab中。
那么,这个随时间而改变的分力数组如何计算呢?
这需要用到惯性力的概念,以及质点的切向加速度和法向加速度的概念。
偏心质量转动时候的惯性力如下
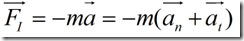
上式中,加速度分为两项,一项是该偏心质量的法向加速度,一项是切向加速度。
由于在ANSYS中不能施加矢量,而只能在直角坐标系中的坐标轴方向上分别施加加速度。上图中的转轴是Z轴,因此,该矢量只在X,Y两个方向有投影。投影如下:
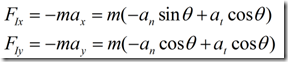
上式中,法向加速度和切向加速度如下
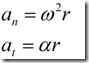
将这两个加速度代入惯性力的两个分量中可以得到
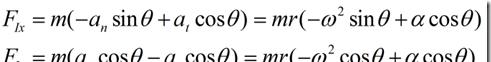
在上述两式中,距离r是已知量,要完全确定FIX,FIY,还需要确定此时的角速度,此时的转角以及此时的加速度。
假设在启动瞬间是匀加速转动,在4秒内速度增加到5000RPM,则加速度是
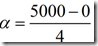
而任一瞬时的角速度是
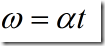
任一瞬时的转角是
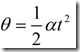
将上述转角,角速度,角加速度代入惯性力的两个分量表达式中,就可以求出这偏心质量导致的惯性力的这两个分量。
因此,施加旋转力的步骤是:
(a)计算加速度。根据(5):匀加速度转动的假设。
(b)计算角速度。根据(6):角速度=角加速度×时间
(c)计算转角。根据(7):转角=1/2*角加速度×时间的平方
(d)计算M*R。这是一个组合量=质量×偏心质量到转轴的距离,并无实际的意义
(e)计算惯性力的两个分量。根据(4):利用(a)(b)(c)(d)的结果。
相关标签搜索:基于ANSYS经典界面的偏心圆盘启动的转子动力学分析-1(瞬态动力学分析) Ansys有限元培训 Ansys workbench培训 ansys视频教程 ansys workbench教程 ansys APDL经典教程 ansys资料下载 ansys技术咨询 ansys基础知识 ansys代做 Fluent、CFX流体分析 HFSS电磁分析 Abaqus培训






