船舶与海洋工程结构物疲劳断裂分析研究现状
2016-12-21 by:CAE仿真在线 来源:互联网
由船海工程的发展趋势,进而引出疲劳裂纹分析在船海工程中;简述了疲劳分析以及断裂力学的研究现状以及存在的一些问题,浅谈对将来发展趋势的一些看法;然后过渡到当前的研究方法,即主要为数值计算方法;对当前数值计算的具体方法进行了概括,并浅谈发展趋势;列举了两个具体例子,即断裂力学原理在疲劳分析中的应用。
海洋产业作为未来世界经济的支柱产业之一,发展潜力非常巨大,世界海洋产业总产值逐年大幅上升。其中,随着能源问题的日益突出,海洋油气开发将是海洋工程最主要的应用领域。并且,在发展船舶与海洋工程的同时,由于其技术关联度大,技术含量高,可带动相关行业的科技进步和产业发展。因此,船海工程有相当广阔的发展前景。
当前,船舶与海洋工程发展趋势主要表现在以下方面。其一,船舶发展趋势是大型化、高速化。技术性能的不断提升促进了船舶运载能力和航速的大幅提高,由此船舶经济性、安全性、环保性明显提高。其二,设计方法不断进步,现代造船模式取代传统造船模式,建造技术装备也在不断发展。其三,海洋工程装备深水化。国外从事海洋工程开发已有一百多年的历史,积累了丰富的经验。发达国家研究的一些深海探测器可达水深已超过万米。
船海工程蓬勃发展,船海结构物发生事故的几率也大大增加。大型远洋船舶发生海损事故已是屡见不鲜。海洋环境复杂多变,海浪、大风、潮流、冰雪、海水腐蚀、地震、微生物、碰撞事故等,都会对海洋平台等结构物造成极大的破坏。更重要的是,船海工程结构物主要采用焊接工艺,由于焊接工艺的特点,焊缝本身不可避免地存在各种缺陷。在各种交变载荷的作用下,这些应力集中区更有可能发生疲劳破坏,造成灾难性的事故。因此,疲劳断裂分析的理论及应用领域和形式的发展就显得非常关键。
2.1 基本概念
载荷值随时间作周期性或非周期性变化的载荷成为交变载荷,由于载荷的变化使试件或构件的材料内产生随时间变化的交变应力与交变应变。经足够的应力或应变循环作用后,损伤累计可使试件或结构材料产生裂纹,直至疲劳破坏。试件抵抗疲劳失效的能力成为材料的疲劳强度;结构抵抗疲劳失效的能力成为结构的疲劳强度。
疲劳失效有以下特征:疲劳破坏是一个累积损伤的过程,其失效过程都经历裂纹萌生、扩展和瞬时断裂三个阶段。不论构件是脆性材料还是塑性材料,疲劳破坏在宏观上常表现为无明显塑性变形的突然断裂,断口为脆性断口。疲劳断口可以看到明显的裂纹源、裂纹扩展区(光滑断面)和瞬时断裂区(粗糙断面)。
在工程中应用的疲劳分析方法可以分为三大类:S-N曲线法、断裂力学方法以及可靠性分析方法。
2.2 S-N曲线法、断裂力学方法
经典的疲劳分析方法基于S-N曲线和Palmgren-Miner线性累积损伤准则,用循环应力范围或塑性应变范围或总应变范围来描述疲劳破坏寿命。与S-N曲线法不同,疲劳分析的断裂力学方法以“损伤容限”原理作为设计基础。这个基本前提是认为损伤为一切工程构件所固有。疲劳寿命则定义为主裂纹从原始尺寸扩展到某一临界尺寸所需的疲劳循环次数或时间。采用断裂力学方法时,需要应用断裂力学的裂纹扩展经验规律。自从具有里程碑意义的PARIS公式提出之后,基于裂纹扩展规律的疲劳分析理论得到了长足的发展。
这两种方法各有优缺点。S-N曲线法可以避免裂纹尖端复杂应力场的分析,断裂力学方法则可更好的反映尺度效应以及可以对一个已有的裂纹提供一个更精确的剩余寿命估算方法。S-N曲线法和断裂力学方法在工程中得到了广泛的应用,成为两种相互补充的基本方法。
2.3 可靠性分析方法
以上这两种方法都是在确定意义上使用的,在分析过程中,有关的参量的都认为是有确定数值。而实际上,工程中涉及到疲劳的有关因素都是随机的。比如,载荷、材料的随机性等。为此,可靠性方法开始被用来进行寿命评估。在该理论中,影响结构疲劳寿命的不确定因素都用随机变量或者随机过程来描述。一个结构的的疲劳寿命合格与否,用服役期内不发生疲劳破坏的概率来衡量。对于受大量不确定因素影响的工程结构的疲劳问题,用结构疲劳可靠性理论来加以研究是非常适当的。
虽然疲劳可靠性方法从理论上是最完善的,可以更合理的描述实际结构中的各种不确定因素,等价符合客观事实。但在工程实践中,由于缺乏充分的统计数据资料,使得可靠性分析中最关键的概率模型的建立也存在很大的分散性,这成为阻碍可靠性分析在工程实际中推广的重要原因。
因而目前常用的海洋工程疲劳强度分析还是主要采用操作起来简单的S-N曲线法,并结合断裂力学方法。
3.1 断裂力学的产生
长期以来,工程上对结构或构件的计算方法,是以结构力学和材料力学为基础的。通常都假定材料是均匀的连续体,没有考虑客观存在的裂纹和缺陷,计算时只要工作应力不超过许用应力,就认为结构是安全的,反之就是不安全的。安全系数并未考虑到其他失效形式的可能性,例如脆性断裂或快速断裂。普遍认为,选用较高的安全系数就能避免这种低应力断裂。然而,实践证明材料存在缺陷或裂纹的结构或构件,在应力值远低于设计应力的情况下就会发生全面失效。人们逐渐意识到,对含有裂纹的物体必须作进一步的研究。断裂力学就是在这个基础上产生的。
断裂力学从宏观的连续介质力学角度出发,研究含缺陷或者裂纹的物体在外界条件作用下宏观裂纹的扩展、失稳开裂、传播和止裂规律。断裂力学的研究方法是:从弹性力学方程或弹塑性力学方程出发,把裂纹作为一种边界条件,考察裂纹顶端的应力场、应变场和位移场,设法建立这些场与控制断裂的物理参量的关系和裂纹尖端附近的局部断裂条件。
经典断裂力学的三个主要分支是:线弹性断裂力学、弹塑性断裂力学、断裂动力学。
3.2 线弹性断裂力学
Griffith通过研究,提出裂纹扩展的能量准则。能量理论将裂纹失稳扩展的临界条件表示为GI=GIc(GI微应变能释放率),即脆性断裂的G准则。GIc是材料常数,表征材料对裂纹扩展的抵抗能力,由试验确定。
G.R.Irwin用弹性力学理论分析了裂纹尖端应力应变场后提出了三种类型裂纹(张开型、滑移型、撕裂型)尖端的应力场与位移场公式。公式中定义了一个包含一个应力强度因子K,对应三种裂纹分别为KⅠ、KⅡ、KⅢ。在线弹性断裂力学中,它是很重要的力学量,用来判断裂纹是否将进入失稳状态的一个指标。以应力强度因子表示的裂纹失稳扩展临界条件为:K=KIC ,称为K准则。KIC为裂纹临界状态下的应力强度因子,称为断裂韧度,也表示材料对于断裂的抵抗能力。
在弹性条件下,

,因此对于线弹性断裂力学问题,采用G准则和K准则是等效的。
3.3 弹塑性断裂力学
由于裂纹尖端应力高度集中,在裂纹尖端附近必然首先屈服形成塑性区域。对于中、低强度钢的中小型结构件,薄壁结构,焊接结构的拐角和压力容器的接管处,在裂纹尖端附近,发生大范围屈服或全面屈服。这时,线弹性断裂力学的结论不再适用。由此研究大范围屈服断裂已成为发展弹塑性断裂力学的迫切任务。
Wells在大量实验的基础上,提出了弹塑性条件的断裂准则,COD准则:当裂纹尖端张开位移

达到临界值

时,裂纹将开裂,即

=


是材料弹塑性断裂韧性指标,为材料参数。
1968年,Rice提出了J积分理论。以J积分为常数并建立断裂准则。J积分是围绕裂纹尖端作闭合曲线的积分。J积分与裂纹扩展力GI的物理意义相同,进而建立J准则:当围绕裂纹尖端的J积分达到临界值JC时,即J=JC时,裂纹开始扩展。
COD准则应用到焊接结构和压力容器的断裂安全分析上非常有效,而且应用时比较简单,因而工程上应用较为普遍。J积分准则理论根据严格,定义明确,但在计算和实验上比较复杂。
弹塑性断裂力学的重要成就是HRR解。硬化材料I型裂纹尖端应力应变场的弹塑性分析是由Hutchinson,Rice,Rosengren解决的。它建立了塑性应力强度因子与J积分的定量关系,表明J积分可以作为描述硬化材料中裂纹尖端应力应变场强度的参量。HRR理论是J积分作为断裂力学判据的理论基础。
3.4 断裂动力学
70年代,Sih与Loeber导出了外载随时间变化而裂纹是稳定情况的渐进应力场与位移场。Rice等多人先后导出了裂纹以等速传播情况的渐进应力场与位移场,并提出了裂纹稳定而外载随时间迅速变化情况下的裂纹开裂准则。
3.5 断裂力学理论存在的一些问题及展望
经典断裂力学是建立在奇异性基础上的,即均基于裂纹顶端应力与应变为无限大的模式展开的。奇异性理论一直延续至今。但是奇异性断裂力学在物理上存在本质的缺陷。实际发现的裂纹,裂纹顶端曲率半径为有限值,裂纹顶端的应力应变也为有限值。这样,基于数学尖端裂纹和应力奇异性的物理量缺乏坚实的物理基础。为了完善理论,可采用比较符合实际的半圆形顶端的钝裂纹,而这又需要金相断裂力学的发展。
由于断裂力学能对材料和结构的安全性进行预测与估算,因而愈来愈受到重视。目前,线弹性断裂力学发展较为成熟,在工程实际中已经得到应用。弹塑性断裂力学虽然取得了一些进展,但仍有许多尚待深入研究的问题,它是当前断裂力学主要研究方向之一。断裂动力学,对于线性材料还有待完善,对于非线性材料,尚处于研究初期,也是断裂力学的主要研究方向。
在疲劳断裂分析的研究中,最主要的三大研究方法就是:理论、试验和数值计算。但是,只有极少数简单、特殊的断裂力学问题存在解析解,而试验方法操作起来比较麻烦,而且经济性不佳,因此绝大多数工程问题都借助数值计算的方法来进行研究。随着研究的日益深入,需要求解的问题日趋复杂化和多样化。使得如何建立高效、高精度的计算方法成为学者们研究的热点。由于计算机科学、计算数学和力学等学科的不断发展,用于解决疲劳断裂问题的数值计算方法不断涌现,它们正成为推动疲劳分析和断裂力学发展的有力工具。
4.1 有限元法
普遍认为,有限元法的出现是计算力学诞生的标志。有限元法是建立在传统的Ritz法的基础上,利用变分原理导出代数方程组求解。它将连续介质离散成有限个单元来进行数值计算。有限元法实现了统一的计算模型、离散方法、数值求解和程序化设计方法,从而能广泛地适应求解复杂结构的力学问题。有限元法从诞生至今得到了迅猛的发展,成为用于结构和固体力学问题的首选方法。
当前断裂力学用有限元法取得了极大的研究进展。比如,采用自适应有限元法确定裂纹尖端的塑性区,在有限元法的基础上建立随机分析,用于动态问题的空-时有限元法等等。
4.2 其他数值计算方法
由于有限元法同时也存在缺陷,比如随着计算精度要求的提高,有限元网格的划分将十分困难,计算量也会十分庞大。因此,学者们在研究过程中又逐渐创立了其他数值计算方法。主要有:边界元法、无网格法、数值流形方法、小波数值法等,此外还有位移不连续法、超奇异积分方程法、加权残数法、有限差分法扩展有限元法等,都取得了进展。
4.3 数值计算方法的发展趋势
(1) 并行数值计算方法。该方法是在工程计算规模大幅增加与计算机能力受到限制的矛盾日益突出的情况下产生的。
(2) 解析法与数值法相结合。解析法与数值法相互结合、相互渗透将为研究提供一系列高效算法。
(3) 多种计算方法有机结合。结构的形式很少是单一的,多种方法的耦合将会提高运算精度以及运算速度。
(4) 数据处理自动化。为了提高效率,自适应有限元法和网格的自动划分与技术更新仍将是有限元研究中的一个热点。
(5) 耦合场中的数值计算在一些领域也将越来越重要。
5.1 海洋平台管节点疲劳性能研究
笔者正在完成的毕业设计的题目是:“导管架式海洋平台管节点疲劳强度分析”。以下是我在学习过程中遇到的一个实例,用断裂力学方法来求解管节点的疲劳寿命。
1. 基本原则
从Paris公式 da/dN=c

出发,则 Np=

式中,c、m为材料常数,由材料、焊接构件及管节点试验综合分析给出,建议:c=4.764

10-12,m=3.152;

=Y

式中,Y为管节点形状因子,由管节点试验和有限元计算给出。Y=A

2. 基型管节点形状因子
基型管节点形状因子Y
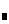
由基型管节点试验及有限元计算分析给出。不同载荷下形状因子为
轴向载荷:
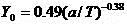
面内弯曲载荷:

面外弯曲载荷:

基型管节点形状因子Y0见图
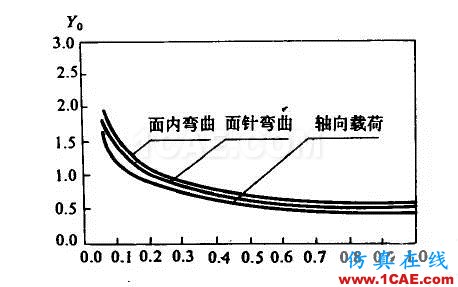
基型管节点形状因子Y0
3. 修正因子M
(1) 厚度修正因子Mt
在裂纹扩展阶段,厚度修正因子为 Mt=(T/T0)0.25
(2) 焊缝修正因子Mw
焊缝局部应力集中对裂纹萌生影响很大,对裂纹扩展速率也有明显影响,必须考虑其对形状因子的修正。焊缝修正因子为 Mw=

(3) 应力分布修正因子M

应力分布不均匀性由几何参数决定,其修正因子为

M

(4) 海水自由腐蚀修正因子 MH
海水腐蚀对管节点裂纹扩展速率影响同应力水平有关,海水自由腐蚀因子为
MH=

(5) 阴极防护修正因子

4. 管节点形状因子
建立在基型管节点形状因子Y0修正的基础上,管节点形状因子为


为验证修正可靠性,把修正结果同试验结构相对比。
自由腐蚀,在

下
修正法:

试验法:

阴极防护:在
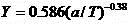
下
修正法:

试验法:

可以看出修正结果同试验结果相一致,因此修正方案可靠。
由Paris公式
Np=


取T
5.2 海洋平台结构的安全寿命评估与维修决策
此部分内容来源于黄小平、崔维成、王庆丰所著《海洋平台结构的安全寿命评估与维修决策研究》。
海洋平台结构复杂,造价昂贵,一旦发生事故会造成不可估量的经济损失。因此保证安全性以及延长其服役期就显得至关重要。以上学着提出地基于疲劳断裂力学控制的评估方法适合于任何类型、处于任意使用阶段的结构安全寿命评估。其显著特点是可以方便地通过检测对评估结果进行验证,该特点可显著提高预报结果地可靠性和可信性。
该法克服了传统地安全寿命法的不足,不需要对平台结构过去的受载历史进行了解,只需知道目前平台结构的受损程度,以及今后平台受载情况,即可对海洋平台进行安全评估和断裂控制,并进一步计算其疲劳寿命。
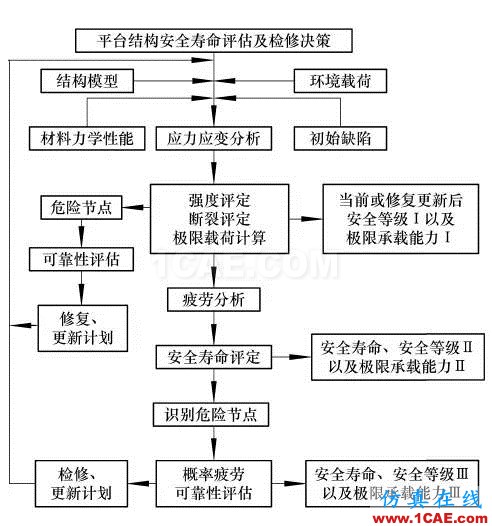
海洋平台安全寿命评估及检修决策图
本文介绍了船海工程的发展趋势,进而引出疲劳裂纹分析在船海工程中的应用。接下来简述了疲劳分析以及断裂力学的研究现状以及存在的一些问题,然后浅谈了对将来发展趋势的一些看法。然后过渡到当前的研究方法,即主要为数值计算方法。对当前数值计算的具体方法进行了概括,并浅谈发展趋势。在这之后,列举了两个具体例子,即断裂力学原理在疲劳分析中的应用,这也是疲劳分析的一个正在发展的重要方法。
最后,对船海工程疲劳断裂分析再次进行一下展望。第一部分已经提到过,由于船海工程加工工艺的特点,即焊接工艺的特点,疲劳断裂在船海工程中的应用将会有广阔的天地。理论的发展和应用离不开工程实际的需要,随着船海工程的发展需要,也必将促使学者们不断研究提出新理论,完善经典理论,并借助计算机科学的发展,大幅度提高数值计算的精度和效率。
相关标签搜索:船舶与海洋工程结构物疲劳断裂分析研究现状 Ansys有限元培训 Ansys workbench培训 ansys视频教程 ansys workbench教程 ansys APDL经典教程 ansys资料下载 ansys技术咨询 ansys基础知识 ansys代做 Fluent、CFX流体分析 HFSS电磁分析 Abaqus培训






