有限元分析软件ANSYS在机械设计中的应用

2017-01-23 by:CAE仿真在线来源:互联网

在机械设计中运用ANSYS软件进行有限元分析是今后机械设计发展的必然趋势,将有限元方法引入到机械设计课程教学中,让学生参与如何用有限元法来求解一些典型零件的应力,并将有限元结果与教材上的理论结果进行对照。这种新的教学方法可以大大提高学生的学习兴趣,增强学生对专业知识的理解和掌握,同时还可以培养学生的动手能力。在机械设计课程教学中具有很强的实用价值。

前言:

机械设计课程是一门专业基础课,其中很多教学内容都涉及到如何求取零件的应力问题,比如齿轮、v带、螺栓等零件。在传统的教学过程中,都是根据零件的具体受力情况按材料力学中相应的计算公式来求解。比如,在求解齿轮的接触应力时,是把齿轮啮合转化为两圆柱体的接触,再用公式求解。这些公式本身就比较复杂,还要引入各种修正参数,因此我们在学习这些内容时普遍反映公式难记,学习起来枯燥乏味,而且很吃力。

近年来有限元法在结构分析中应用越来越广泛,因此如果能将这种方法运用到机械设计课程中,求解一些典型零件的应力应变,并将分析结果和教材上的理论结果进行对比,那么无论是对于提高学生学习的热情和积极性,增强对重点、难点知识的理解程度,还是加强学生的计算机水平都是一件非常有益的事情。

由于直齿圆柱齿轮的接触强度计算是机械设计课程中的一个重要内容,齿轮强度的计算也是课程中工作量最繁琐的部分。下面就以渐开线直齿圆柱齿轮的齿根弯曲疲劳强度的计算为例,探讨在机械设计课程中用ANSYS软件进行计算机辅助教学的步骤和方法,简述如何将有限元方法应用到这门课程的教学中。

1.传统的直齿圆柱齿轮齿根弯曲疲劳强度的计算

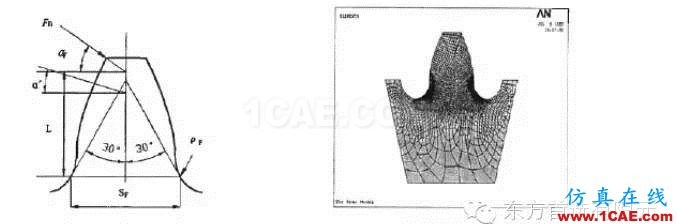
传统方法把轮齿看作宽度为b的矩形截面的悬臂梁。因此齿根处为危险剖面,它可用30。切线法确定。如图l所示。作与轮齿对称中心线成30。角并与齿根过渡曲线相切的切线,通过两切点作平行与齿轮轴线

的剖面,即齿根危险剖面。理论上载荷应由同时啮合的多对齿分担,但为简化计算,通常假设全部载荷作用于齿顶来进行分析,另用重合度系数E对齿根弯曲应力予以修正。

由材料力学弯曲应力计算方法求得齿根最大弯曲应力为:

式中:K是载荷系数;T是齿轮传递的名义转矩;b是齿宽;d是齿轮分度圆直径:m

是模数;Yfd是齿形系数;Ysa是应力修正系数;Yg是重合度系数。

2.用有限元法对直齿圆柱齿轮齿根弯曲疲劳强度进行计算

(1)建立几何模型在ANSYS软件中,根据圆柱直齿轮的齿廓和过渡曲线坐标建立几何模型。齿轮具体参数为分度圆压力角是20。,模数是3.5mm,齿顶高系数是1.0,顶隙系数是O.25,齿数是23。 (2)约束条件和边界处理当轮齿受力时,齿轮体不可能是绝对刚性,与轮齿相连部分也有变形,当离齿根的深度大于或等于模数的4.5倍时基本上不再受影响,可以近似看作该处的实际位移为零;另外,两侧齿间中点处的位移很小,可以忽略不计,也可以认为该处的实际位移为零,这样即可划定其零位移约束边界。模型中,可在零位移约束边界的各节点处安装铰支座来实现。因此,对于单齿模型,若齿轮的模数为m,则零位移约束边界的范围为:横向宽取5m,纵深方向距齿根圆弧最低点取4.5m。

(3)单元类型的选择在有限元计算模型中,选择具有八个节点二十四个自由度的四边形单元。这是因为齿轮轮齿齿廓形状为渐开线,采用四边形单元能较好地逼近齿轮齿廓的曲边形状;八节点四边形等参单元是采用通过边界上三个节点的二次抛物线来局部近似代表齿根曲线的,这与三角形单元以直线边界来代表曲线边界相比,显然大大地提高了对原边界曲线的拟合性,减少了在离散化过程中,因求解区域的近似处理带来的误差。

(4)进行网格划分根据齿轮上应力分布的情况,在应力梯度较大的齿根区域网格划分的细密一些,在应力变化比较平缓的区域网格划分的稀疏一些。划分网格后ANSYS模型如图2所示。

(5)轮齿的作用载荷由于当载荷作用在在单齿啮合上界点处时,齿根弯曲应力达到最大值,故将载荷置于齿轮单齿啮合上界点。当齿轮传动功率P=45kW,齿轮转速n=1000r/min时,齿宽b=30mm时,传递的名义转矩T=429N·m。水平与垂直分力分别为:

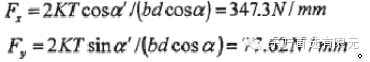
式中,a’是单齿啮合上界点的载荷角,如图1所示。

(6)求解应用ANSYS软件对所建立的模型进行分析。弹性模量取为

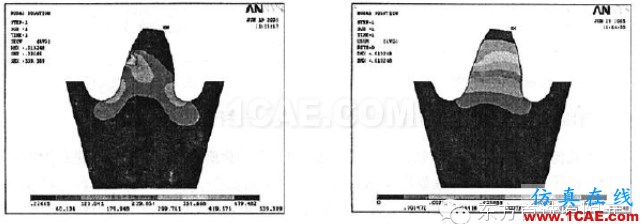
泊松比取为0.25。所得的应力等值线如图3所示,由此图可以看出应力的分布情况。轮齿的中间和上部的应力较小,齿根过渡曲线处应力较大,最大应力出现在30。切线法所确定的危险截面附近,由中间向两边齿侧逐渐增大。而且通过ANSYS软件还可以分析齿轮综合位移以及齿廓任意点受载时的应力和位移等值线,载荷作用于节点时应力和位移等值线如图3和图4所示。

3.传统算法与有限元算法的比较

传统算法的初始条件见表1,功率和转速与有限元法相同,载荷系数取k=1.28,代入式(1)

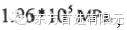
可得齿轮齿根危险截面弯曲应力,有限元法计算结果

。

在传统算法中,重合度系数Y已经将载荷作用于齿顶时的弯曲应力转换成载荷作用于单齿啮合上界点时的弯曲应力;而有限元算法中,是将载荷直接加在单齿啮合上界点,故可以直接比较结果。可见有限元计算结果与传统方法计算结果误差为6.4%。

由此可见,ANSYS软件在机械设计中的精确度是很高的,而且人工计算量比传统方法小很多。除此之外,ANSYS软件还可以对一些特殊零件进行分析计算,如复合型轴承、复杂曲面的箱体等。而这些是传统方法无法完成的。比如现在新兴的一种双压力角非对称齿廓渐开线齿轮,具有承载能力高,振动低,重量轻等优点。由于非对称齿轮两边压力角不同,故无法通过传统方法计算分析,而用有限元法只要输入齿廓坐标建模就可以很轻松地对其进行计算分析。