中国比西方进步704年!横梁高宽比ANSYS分析【转发】
2017-02-22 by:CAE仿真在线 来源:互联网
导读:刊行于1103年的《营造法式》规定的梁木高宽比h/b=3:2=1.5,介于强度最大和刚度最大之间,具有极高的科学性,比西方早704年。

一、中国力学史札记:横梁高宽比
众所周知,确定横梁高宽比数是中国古代重大力学成就之一。早在公元前5000年,浙江河姆渡遗址中梁木和木枋的高宽比h/b大约是4:1。
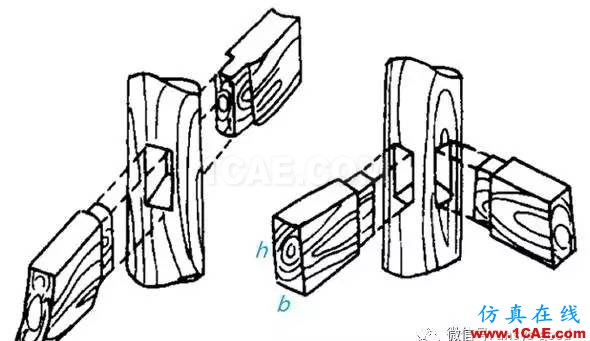
梁木断面及其安装方式

浙江河姆渡遗址,木梁高宽比为4:1
记载西周末年至春秋时期各国史事的《国语》中,述及鲁成公16年(公元前575年)鲁大夫公孙婴齐(又作“子叔声伯”)的一段话:
“吾闻之,‘不厚其栋,不能任重’。”老亮先生最早将此文中的“厚”译为矩形梁的高,“厚其栋”就是要加大梁的高度,它表明,春秋时期的建筑师凭经验知道,增大梁木断面的高度对于承重的重要性。春秋迄宋代,建筑师李诫才在其著《营造法式》中作出横梁高宽的科学比数3:2。然而,从春秋至宋的千余年间,人们对这比数的认识如何发展的?历史文献是否对此留下空白?恰好,在古代数学著作中可窥知一二。

习近平在中央统战工作会议上
《国语》用典“不厚其栋,不能任重”
《九章算术》中有一道算题、涉及从圆木中锯取矩形木问题,它写道:
“今有圆材,径二尺五寸。欲为方板,令厚七寸,问广几何 ?
答曰:二尺四寸”。
刘徽注云:“此以圆径二尺五寸为弦,板厚七寸为勾,所求广为股也。”

九章算术,成于公元一世纪左右
众所周知,中国古代数学著作,尤其是隋唐之前的数学实用性甚强。该算题很可能来自营匠的实践经验,而加工如此巨大木料,算题本身虽未明言其用途,但它是为横梁加工而总结的营匠师徒的口传秘诀,亦不无可能。将这样的矩形木作梁,其高宽比则为3.43:1或3:0.875。这比数较之阿姆渡的梁枋进步多了。它是战国迄汉代木构建筑中的梁木加工制度,亦未可知。甚至于宋代,蒲田玄妙观三清殿(建于1009年)中还有高宽比(为3.05:1)极其近似的梁木。

浙江蒲田玄妙观三清殿

浙江蒲田玄妙观三清殿,木梁高宽比为3.05:1
在汉代之后,魏晋南北朝期间,人们曾以方木作梁。成书于刘宋末的《张邱建算经》有一道算题是这种方梁的反映。它写道:
“今有圆材,径头二尺一寸,欲以为方,问各几何?
答曰:一尺五寸。”
尚需指出,解这道题是以“方五斜七”为据的。这个约略的勾股定理就是来自营匠的经验数值。而方形梁木,不仅此时有,直到宋代也偶有所用。如建于964年的华林寺大殿中有0.91:1的梁。这比值很接近方形梁。

福建华林寺大殿

福建华林寺大殿正间横架,接近方梁
由此可见,至少汉唐之间,人们对横梁高宽比的认识尚未成熟。此时期,既有3.43:1的矩形梁,也有方形梁。唐宋年间,据古建筑实测数据,此时梁木多为矩形梁,而高宽比数在3:1.1至3:1.94之间不等。李诫的《营造法式》是唐宋年间营建实践的总结,他规定的3:2不仅科学,且规范化了,对后世营造也起了重大影响。

李诫(1035年-1110年)
中国古代土木建筑家
李诫(1035年-1110年),字明仲,郑州管城县(今河南新郑)人。中国古代土木建筑家、《营造法式》一书的编纂者。

《营造法式》刊行于1103年
规定梁木高宽比3:2
《营造法式》编于北宋熙宁年间(1068-1077),成书于元符三年(1100),刊行于宋崇宁二年(1103年),是李诫在两浙工匠喻皓的《木经》的基础上编成的。是北宋官方颁布的一部建筑设计、施工的规范书,这是我国古代最完整的建筑技术书籍,标志着中国古代建筑已经发展到了较高阶段。
二、西方近代科学:横梁高宽比
英国的托马斯·杨(Thomas Young,1773-1829),于1807年著《自然哲学与机械技术讲义》一书中指出:矩形木梁的合理高宽比为




托马斯·杨(Thomas Young,1773-1829)
刊行于1103年的《营造法式》规定的高宽比3:2 = 1.5,介于强度最大和刚度最大之间,具有极高的科学性,比西方早704年。
三、问题描述
如图所示梁木,矩形横截面由直径为400mm的圆木锯取而成,高宽比取1.5,高度h=332.8 mm,宽度b=221.9 mm。木材的弹性模量E = 10 GPa,泊松比u =0.3。梁木的长度为6m,梁受均布载荷q =5 kN/m作用。梁木的两端约束处理成铰支,计算梁木的应力和变形。

问题分析:
受弯曲变形,用梁单元BEAM188建模分析。梁单元的单元属性有单元类型、截面属性和材料属性。ANSYS无单位,需自己统一,本次采用N、mm和MPa单位制。由于BEAM188是空间梁,具有3个平动自由度和3个转动自由度,对于图示的简支梁,在A点约束UX、UY、UZ和ROTX,在B点约束UY和UZ。约束A点的UX是为了防止X方向的刚体平动,约束ROTX是为了防止刚体转动。
四、计算结果分析
1.结果列表
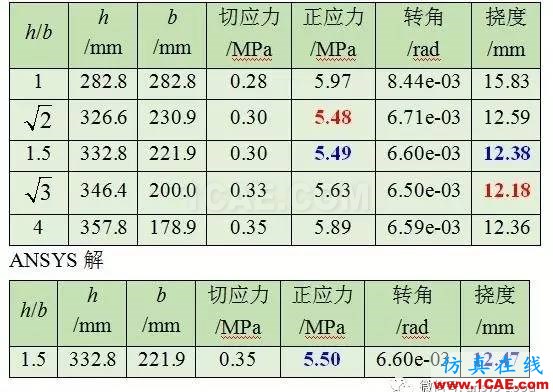
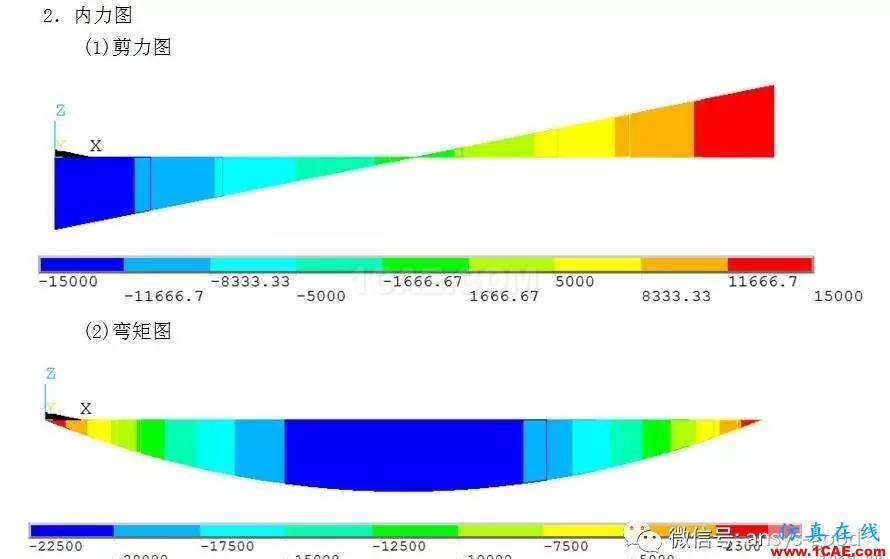
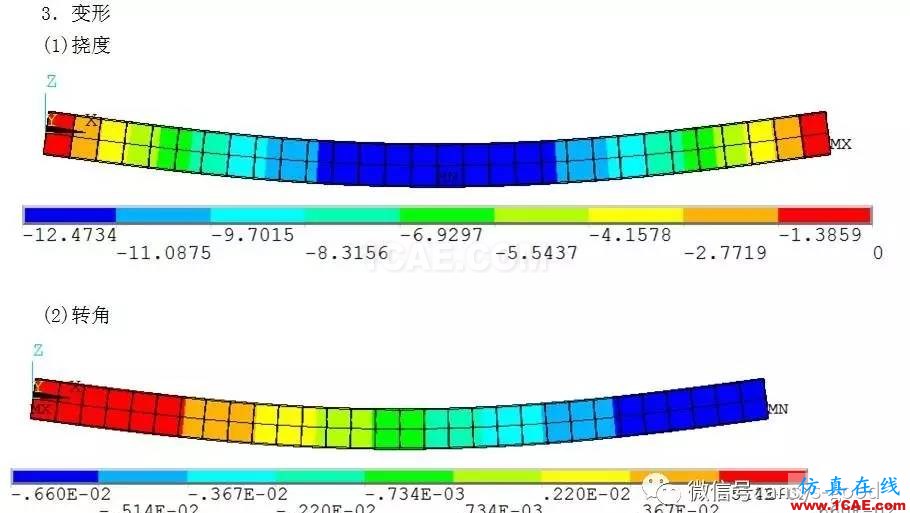
五、理论计算
参考教材:刘鸿文.材料力学(第5版)[M]. 北京:高等教育出版社,2011: 110-209.

六、GUI步骤
1.进入ANSYS
程序→ ANSYS → ANSYS Product Launcher → 改变working directory到指定文件夹 → 在jobname输入:file→ Run。
2.定义工作文件名及工作标题
(1)定义工作文件名:UtilityMenu > File > Change Jobname → Change Jobname → 输入文件名file→ OK。可不用输入,默认为file。
(2)定义工作标题:UtilityMenu > File > Change Title → Change Title → 输入Beam→ OK。可不用输入。
3.定义单元属性
(1)定义单元类型:
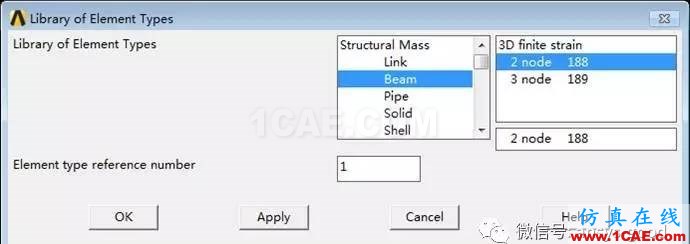
①指定BEAM188单元:MainMenu >Preprocessor >Element Type >Add/Edit/Delete →Add →在左列表框中选择Beam,在右列表框中选择2 node 188 →OK。
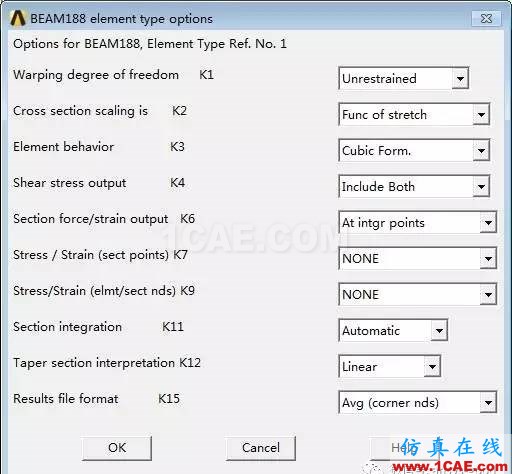
②设置单元选项:Options→Element behavior K3:CubicForm(三次形函数);Shear stress output K4:IncludeBoth →OK。默认情况下Elementbehavior是一次形函数,Shear stress output只输出扭转切应力,不输出剪力产生的切应力。因此,需做如上修改,改成三次形函数和输出切应力。
(2)定义截面:MainMenu >Preprocessor >Sections >Beam >Common Sections →ID:1,在Sub-Type下拉框选择矩形截面,B:221.9,H:332.8,NB:4,NH:4 → Meshview →Meshview →OK。高宽比取3:2,NB和NH是横截面的份数。
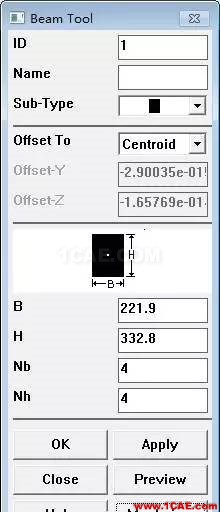
(3)设置材料属性:MainMenu > Preprocessor > Material Props > Material Models → Structural→Linear →Elastic → Isotropic → EX:10e3,PRXY:0.3→ OK。
4.建立几何模型
(1)生成关键点:Main Menu>Preprocessor >Modeling >Create >Keypoints >In Active CS →依次输入关键点的编号和坐标:1 (0,0,0),2 (6e3,0,0)→OK。
(2)创建直线:MainMenu>Preprocessor>Modeling>Create>Lines>Lines>Straight Line→依次拾取1和2,2和3,创建2条直线→OK。
5.划分网格
(1)设置线的单元属性:MainMenu >Preprocessor >Meshing >Mesh Tool →在Element Attributes下方选择Lines Set→ 拾取线1→OK→选择MAT:1,TYPE:1,SECT:1→OK。单元类型编号、截面编号和材料编号只有一种,可默认,不需要指定,此步骤可省略。
(2)设置单元尺寸:MainMenu >Preprocessor >Meshing >Mesh Tool →在Size Controls下方选择Global Set →SIZE:200→OK。每200mm划分一个单元。
(3)划分梁单元:MainMenu >Preprocessor >Meshing >Mesh Tool →Mesh:Lines→ Mesh → Pick All。
(4)打开梁单元的单元形状:Utility Menu>PlotCtrls >Style >Size and Shape →[/ESHAPE]: On。
(5)显示单元:Utility Menu > Plot > Element。
6.施加边界条件
(1)施加约束:MainMenu>Solution>Define Loads>Apply>Structural>Displacement>OnKeypoints →拾取关键点1→ OK → Lab2:UX、UY、UZ和ROTX→ Apply →拾取关键点3→ OK → Lab2:UY和UZ→ OK。
(2)施加均布载荷:MainMenu >Solution >Define Loads >Apply >Structural >Pressure >On Beams →Pick All→ LKEY:1,VALI:5,VALJ:5→ OK。注意单位是N/mm。
施加均布载荷的说明:根据实例中的坐标,均布载荷应在-Z方向施加。
A.打开梁单元的单元坐标系:UtilityMenu>PlotCtrls>Symbols →ESYS:On→OK。
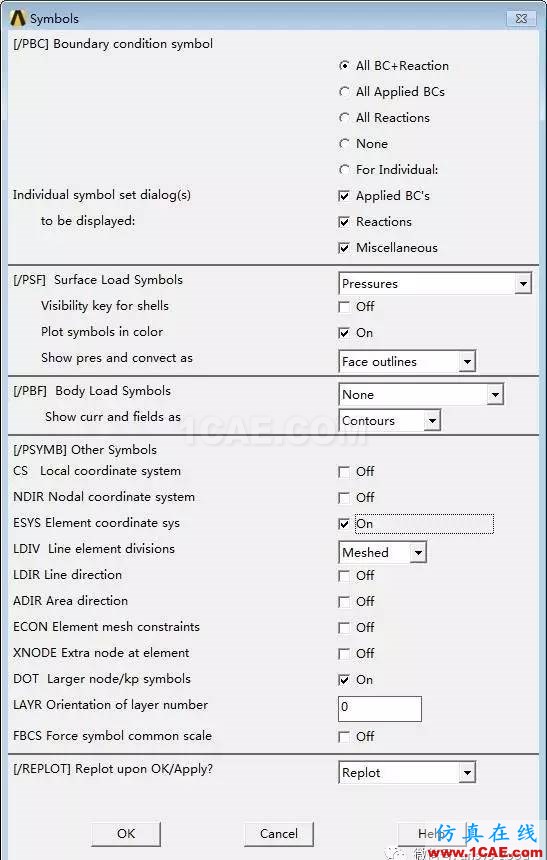
B.检查梁单元的单元坐标系,看不清请把单元形状关掉,检查后再把单元形状打开。单元坐标系的X、Y和Z坐标与整体坐标系相同。经查,该实例的单元坐标系与整体坐标系一致。
C.查看在单元坐标系下施加均布载荷的编号:打开ANSYS帮助→索引中选择Beam188→回车→在Beam188单元说明查看“BEAM188Geometry”说明。可见梁单元坐标系的-Z方向施加的均布载荷的编号为①,数值应是加正值。
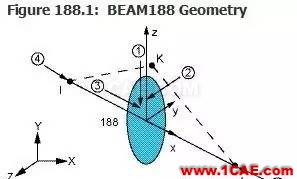
(3)求解前保存模型:UtilityMenu > Files > Save as → 输入Beam_Load.db→ OK。
7.求解
(1)求解:MainMenu > Solution > Solve > Current LS → File > Close → Solve CurrentLoad Step → OK → Solution is done → Close。
(2)保存结果文件:UtilityMenu > Files > Save as → 输入file.db→ OK。
8.后处理
(1)列表查看约束反力:MainMenu > General Postproc > List Results > Reaction Solu → All strucforc F → OK。注意反力的方向,记录数值。
(2)查找定义内力(剪力和弯矩)单元表的方法
①查找定义BEAM188内力单元表的方法:打开ANSYSHelp,搜索BEAM188。
找到BEAM188的单元介绍页面后,页面中查表Table 188.1: BEAM188 Element Output Definitions。表中查找Name:SF:y, z,Definition:Section shear forces,在Name栏中SFz便是剪力。
表中查找Name:My, Mz,Definition:Bending moments,在Name栏中MY便是弯矩。
页面中查表Table 188.2: BEAM188 Item and Sequence Numbers。表中查找OutputQuantity Name:剪力SFz,Item:SMISC,I:5,J:18。弯矩My,Item:SMISC,I:2,J:15。
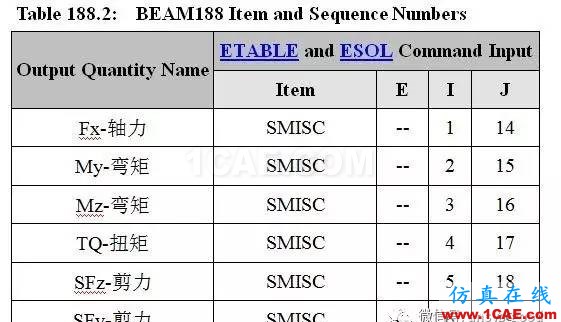
(3)查看各单元剪力,注意剪力的方向
①定义剪力单元表:MainMenu > General Postproc > Element Table > Define Table → Lab:输入SFZ_I→ Item:选择By sequence num → Comb:选择SMISC,在SMISC后面输入“5” →OK → Apply → Lab:输入SFZ_J → Item:选择Bysequence num → Comb:选择SMISC,在SMISC后面输入“18” → OK → Close。
②剪力列表:MainMenu > General Postproc > Element Table > List Element Table → 选择SFZ_I和SFZ_J→ OK → 记录弯矩值 → File → Close。
③剪力云图:MainMenu > General Postproc > Plot Results > Contour Plot > Line ElemRes → LabI选择SFZ_I,LabJ选择SFZ_J→ OK。
(4)查看各单元弯矩,注意弯矩的方向
①定义弯矩单元表:MainMenu > General Postproc > Element Table > Define Table → Lab:输入MY_I→ Item:选择By sequence num → Comb:选择SMISC,在SMISC后面输入“2” →OK → Apply → Lab:输入MY_J → Item:选择Bysequence num → Comb:选择SMISC,在SMISC后面输入“15” → OK → Close。
②弯矩列表:MainMenu > General Postproc > Element Table > List Element Table → 选择MY_I和MY_J→ OK → 记录弯矩值 → File → Close。
③弯矩云图:MainMenu > General Postproc > Plot Results > Contour Plot > Line ElemRes → LabI选择MY_I,LabJ选择MY_J→ OK。
④将弯矩单位N.mm转换成N.m:MainMenu >General Postproc >Element Table >Add Items → LabR:MY_I,FACT1:1e-3,Lab1:MY_I→ Apply → LabR:MY_J,FACT1:1e-3,Lab1:MY_J→ OK。
⑤重新画弯矩云图:MainMenu > General Postproc > Plot Results > Contour Plot > Line ElemRes → LabI选择MY_I,LabJ选择MY_J→ OK。
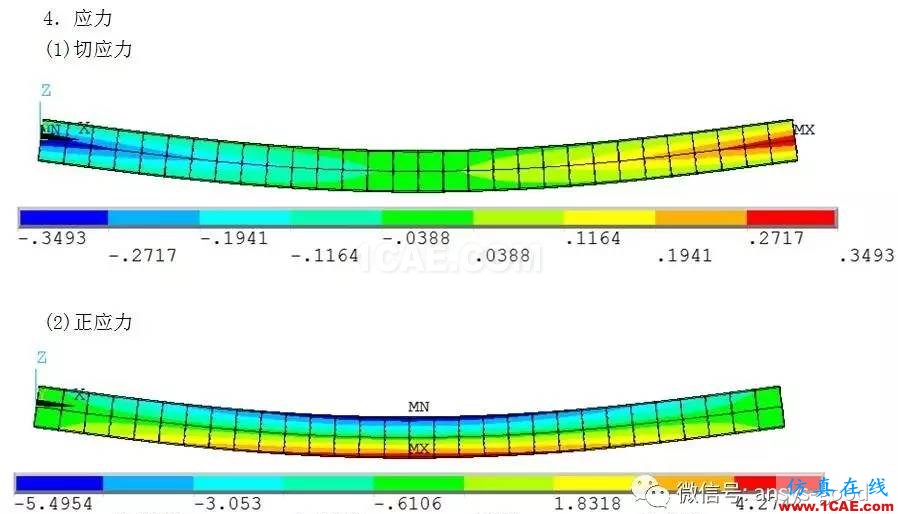
(5)应力云图(切应力和正应力)
①切应力云图:MainMenu >General Postproc >Plot Results >Contour Plot >Nodal Solu → XZShear stress → OK。注意切应力的方向。
②正应力云图:MainMenu >General Postproc >Plot Results >Contour Plot >Nodal Solu →X-Component stress → OK。注意正应力的方向。
(6)弯曲变形(挠度和转角)
①挠度云图:UtilityMenu >Plot >Results >Contour Plot >Nodal Solution → Z - Componentof displacement→OK。注意挠度的方向。
②转角云图:UtilityMenu >Plot >Results >Contour Plot >Nodal Solution → Y - Componentof rotation→OK。注意转角的方向。
9.退出ANSYS软件
Utility Menu> File > Exit → Quit-No Save → OK。
五、APDL步骤
FINISH
/CLEAR,NOSTART !清空数据库
/PREP7
ET,1,BEAM188 !单元类型
KEYOPT,1,3,3 !形函数
KEYOPT,1,4,2 !切应力
MP,EX,1,10e3 !材料属性MPa
MP,PRXY,1,0.3
SECTYPE, 1, BEAM, RECT,,0 !截面属性mm
SECOFFSET, CENT
SECDATA,221.9,332.8,4,4,0,0,0,0,0,0,0,0
K,1,0,0,0, !创建关键点mm
K,2,6e3,0,0,
L,1,2 !创建线
LATT,1, ,1, , , ,1 !线的单元属性
LESIZE,ALL,200, , , , , , ,1 !单元尺寸mm
LMESH,ALL !线分网
/ESHAPE,1.0 !单元形状
/VIEW,1,1,1,1
/VUP,1,Z
FINISH
/SOLU
DK,1,UX !施加位移约束
DK,1,UY
DK,1,UZ
DK,1,ROTX
DK,2,UY
DK,2,UZ
SFBEAM,ALL,1,PRES,5,5, , , , ,0 !均布载荷N/mm
SOLVE !求解
FINISH
/POST1
/UDOC,1,DATE,1 !关闭ANSYS标志和时间
/dev,font,1,Courier*New,400,0,-21,0,0,,, !3号字体
/DSCALE,ALL,20 !变形放大比例
PRRSOL,F !约束反力列表
ETABLE,SFZ_I,SMISC, 5 !定义剪力单元表
ETABLE,SFZ_J,SMISC, 18
/VIEW,1,,,1 !视图
PLLS,SFZ_I,SFZ_J,1,0 !剪力图云图
PRETAB,SFZ_I,SFZ_J !剪力列表
ETABLE,MY_I,SMISC, 2 !定义弯矩单元表
ETABLE,MY_J,SMISC, 15
/VIEW,1,,,1 !视图
PLLS,MY_I,MY_J,1,0 !弯矩图云图
PRETAB,MY_I,MY_J !弯矩列表
SADD,MY_I,MY_I, ,1E-3,1, , !将弯矩单位N.mm转换成N.m
SADD,MY_J,MY_J, ,1E-3,1, ,
PLLS,MY_I,MY_J,1,0 !弯矩图云图
PLNSOL, S,X, 0,1.0 !弯曲正应力
PLNSOL, S,XZ, 0,1.0 !切应力
/GFORMAT,F,12,4, !数据格式
PLNSOL, U,Z, 0,1.0 !挠度
PLNSOL, ROT,Y, 0,1.0 !弯曲角rad
相关标签搜索:中国比西方进步704年!横梁高宽比ANSYS分析【转发】 Ansys有限元培训 Ansys workbench培训 ansys视频教程 ansys workbench教程 ansys APDL经典教程 ansys资料下载 ansys技术咨询 ansys基础知识 ansys代做 Fluent、CFX流体分析 HFSS电磁分析 Abaqus培训






