理论解？数值解？

2017-02-28 by:CAE仿真在线来源:互联网

问题的产生

一长度为4m的40a工字型截面梁两端固支,沿Y轴向下施加120KN/m的均布载荷,求梁的最大正应力以及挠度。(截面参数为b=142mm,h=400mm,t=16.5mm,d=10.5mm,材料弹性模量为2e5MPa,泊松比0.3)

理论解

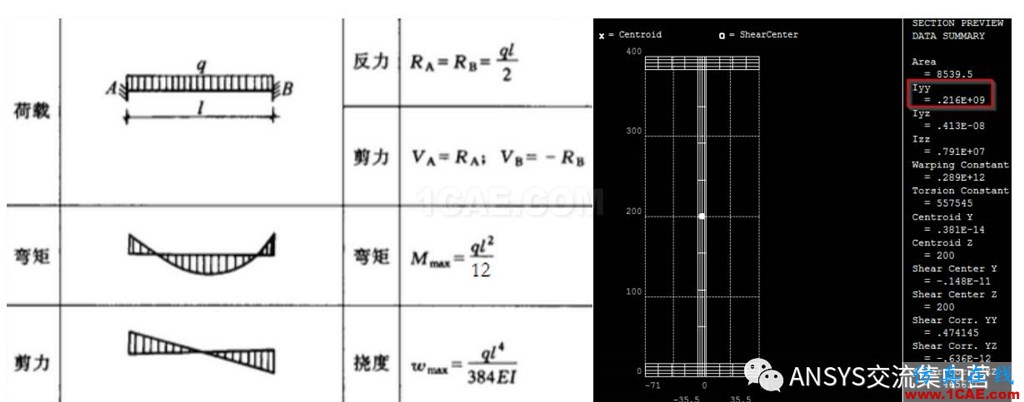
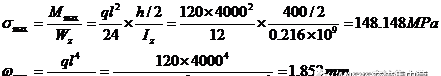
理论解计算结果如下:

最大正应力:148.148MPa 最大挠度1.852mm

数值解

对于ansys来说,现在梁结构分析该毫无疑问直接使用beam18x系列梁单元,这里为了便于绘制弯矩图,使用beam189单元。命令流如下:

finish$/clear$/prep7

!定义截面参数

b=142$h=400$t=16.5$d=10.5

!单元选择与材料、截面建立

et,1,beam189

mp,ex,1,2e5$mp,prxy,1,0.3

sectype,1,beam,I$secdata,b,b,h,t,t,d

!几何模型建立与网格划分

k,1$k,2,4000$k,3,1,1$l,1,2

latt,1,,1,,3,,1$lesize,all,,,50$lmesh,all

/eshape,1$/replot$/solve

!施加约束与载荷

dk,1,all$dk,2,all

sfbeam,all,1,press,120,120

!求解

solve$/post1

!绘制正应力云图与弯矩图

plnsol,s,x

avprin,,0.3$etable,2,smisc,2$etable,15,smisc,15$plls,2,15

分析结果如下

正应力云图(放大100倍)

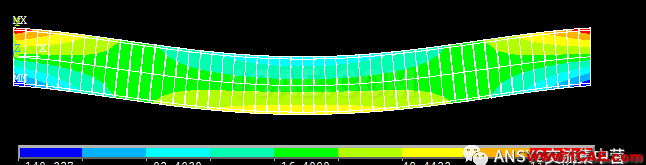
弯矩图(正负是因为单元节点排序问题)

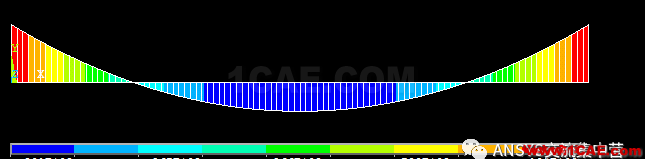
位移云图(放大100倍)

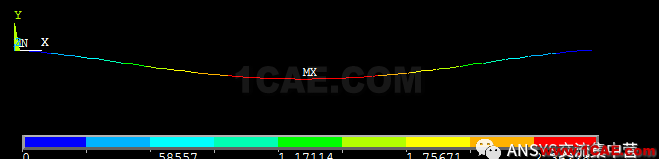
ansys计算结果如下(beam188):

最大正应力:148.327MPa

最大挠度2.635mm

对比结果可以发现数值解的最大应力和理论解接近(已经验证过网格无关性),但是挠度却和理论解误差达到42%。那么问题来了,到底哪个结果更加准确?

问题解决

这里我就单刀直入了,直接使用与该工况最接近的beam3 2D弹性梁单元进行试算。但是由于beam3在12.0版本以后在GUI菜单下已经找不到了,因此要使用该单元需要用命令流定义,只需将上述单元和截面设置更换为下面即可

et,1,beam3

r,1,8539.5,0.216e9,400

计算完以后提取结果如下:

正应力云图(放大100倍)

位移云图(方大100倍)

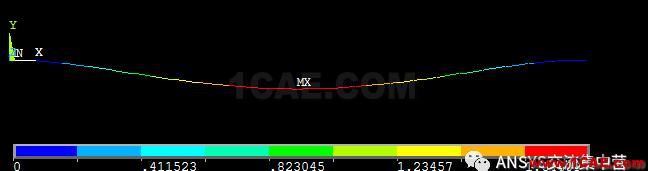
ansys计算结果如下(beam3):

最大正应力:148.148MPa

最大挠度1.852mm

可以看见beam3的结果和理论解完全一样。那肯定有人说,那我用beam3吧,和理论解完全一样。但实际上如果你用实体单元去验证这个计算,你会发现实体单元的结果会跟他门都不一样,但是更接近于beam188计算的结果。实际上也的确应该是这样,因为beam188比beam3考虑的更全面,实体单元比梁单元考虑的更多,因此它的结果肯定也更接近于弹性力学的理论解。Beam3仅仅是因为对单元本身的简化就很严重,因此限制了其精度,而基本材料力学的理论本身迎合而上,所以反而会得到beam3的数值解更加接近材料力学的理论解。

理论解?数值解?

学习有限元的人群有两个极端,有一个极端认为有限元无所不能,就算自己不用掌握高深的力学知识也可以做。有一部分极端认为数值解不可信,只相信实验结果和理论解。但是我个人的观点是,数值解和理论解的比拼本身就相当于田忌赛马。如果你拿理论解的普通马和数值解的好马去比较,那么毫无疑问数值解比理论解更加可靠。如果你拿理论解的好马和数值解的普通马比较,当然理论解更胜一筹。然而,分析者如果没有判断好坏的能力,很有可能宁愿相信一个普通马也不相信一匹好马,而这种能力就是分析者素养很重要的一部分。

我没有偏向于哪一边,反而是这种比较会让人更想去追求更深的理论。所以如果下次手边既有理论解,又有数值解,我肯定不会直接去否定哪一边。首先必须验证有限元解的单元选择是否合适,网格无关性是否验证,材料,工况简化是否合理。同时也必须着手去研究这个理论解的可靠度有多大,能不能找到更加精确的理论解。当两者有一个公平的起点再去比较。当然在本文中我觉得数值解肯定是比材料力学的理论解更可信的。

如果大家对理论解和数值解之间的pk有更好的看法,也欢迎在下面进行讨论。

数值分析是大势所驱,让我们一起为更有价值的分析不断前行!

开放分享：优质有限元技术文章,助你自学成才