ANSYS中模态分析的阻尼法

2017-02-23 by:CAE仿真在线来源:互联网

作者:刘青峰

简单介绍一下ANSYS中模态分析的阻尼法。

正文

在ANSYS中,我们进行模态分析时,Block Lanczos法、Subspace法、Reduced法等方法都是求解:

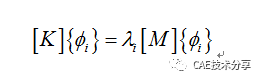
其中:

[K] = 刚度矩阵

[M] = 质量矩阵

{φi} = 特征向量

λi = 特征值

此时只能求解无阻尼系统的特征值和特征向量。如果要想求解有阻尼系统的特征值和特征向量,则要用到阻尼法(damped)或者QR阻尼法(QR damped)。本文将简要的介绍一下阻尼法(damped)的有关理论。用来抛砖引玉,希望大家斧正。

阻尼法求特征值(MODOPT, DAMP)时,特征问题变为二次特征值问题,即:

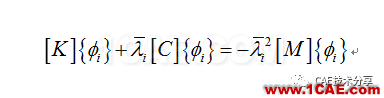
其中:

λi (pa) = sqrt(-λi )

[K] = 刚度矩阵

[M] = 质量矩阵

{φi} = 特征向量

λi = 特征值

其中的刚度矩阵、质量矩阵、阻尼矩阵可以是对称的也可以是不对称的。对于涉及到旋转动力学稳定性的问题,具有陀螺效应的自旋结构,需要求解上述方程以获得如下复数特征值λi (pa):

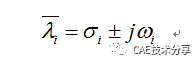
其中:

λi (pa) = 复数形式的特征值

σi = 特征值实数部分

wi = 特征值虚数部分

j = sqrt(-1)

系统的动态响应由下式给出:

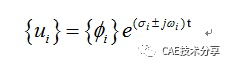
其中:

t = 时间

对于第i个特征值,如果σi为负则系统稳定,为正则不稳定。

该方法的求解算法使用的是Lanczos算法。起始采用四个随机向量{v1}{w1}{p1}{q1},系统矩阵[K][M][C]转换为一个子空间三对角矩阵[B],矩阵B的大小q<=n,接着进行广义Lanczos 双正交变换。[B]矩阵的特征值ui可看做是原始系统的特征值λi (pa)的一个近似值。QR算法被用于提取[B]矩阵的特征值。随着子空间大小q的增加,特征值ui将会收敛于原始系统的特征值λi (pa)的精确解。

需要注意的是:

1. 此方法不执行Sturm序列检查,所以可能会遗漏高端频率。

2.不同节点间存在相差

3.响应幅值 = 实部与虚部的矢量和

4.对于阻尼模态分析,复频率的虚数部分wi会被用于计算单元的动能。