基于 OptiStruct 的车门焊点优化设计
2017-02-27 by:CAE仿真在线 来源:互联网
1 前言
现代轿车承载式车身及四门两盖结构大多由薄板冲压件通过焊点焊接而成,整车焊点约 4000~
5000 个。现阶段焊点主要依据通用的焊接规范和工程经验,参考已有成熟车型进行布置。如果结构 性能满足设计目标要求,则很少对焊点进行优化研究[1]。今年来,随着有限元分析技术、拓扑优化方 法在汽车设计过程中的广泛应用,为焊点布置提供了新的方法。通过焊点结构的拓扑优化设计,可以 找到并减少冗余焊点,选择合理的焊点布置优选方案,降低焊接时间和装配成本[2]。
轿车车门是由具有复杂空间曲面形状的内板、外板以及起局部加强作用的加强板通过冲压和点焊 组合而成的空间薄壁板壳结构。车门作为汽车十分重要而又相对独立的部件,具有隔绝车外噪声,缓 冲来自外部的冲击等舒适性和安全性功能,其刚度、强度性能直接影响整车的品质[3]。
本文以某轿车车门的焊点单元为设计变量,模态、整体刚度和局部刚度等为约束条件,焊点体积 最小为目标函数建立优化模型,应用 HyperWorks/OptiStruct 模块对车门焊点进行拓扑优化,得到不 同密度区间的焊点分布情况,根据优化结果结合工程经验调整车门焊点布置,并对优化前后车门的模 态、刚度、强度性能进行了对比分析。
2 拓扑优化理论简介
拓扑优化技术是结构优化技术中有前景、创新性的技术,是指在给定的设计空间内找到最佳的材料分布,或者传力路径,从而在满足各种性能的条件下得到重量最轻的设计。拓扑优化中常用的拓扑表达形式和材料插值模型方法有:均一化方法、密度法、变厚度法和拓扑函数描述方法。OptiStruct 拓扑优化的材料模型采用密度法(SIMP方法),即将有限元模型设计空间的每个单元的“单元密度(Density)”作为设计变量。该“单元密度”同结构的材料参数有关(单元密度与材料弹性模型 E 之间具有某种函数关系),0~1 之间连续取值,优化求解后单元密度为 1(或靠近 1)表示该单元位置处 的材料很重要,需要保留;单元密度为 0(或靠近 0)表示该单元处的材料不重要,可以去除,从而 达到材料的高效利用,实现轻量化设计[4]。拓扑优化的数学模型可以用下式表示:

3 车门焊点优化模型建立
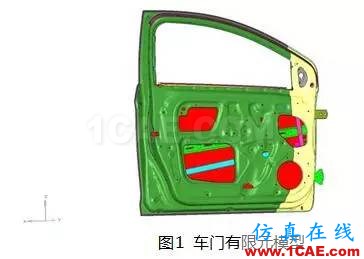
3.1 车门有限元模型建立
根据企业内部的乘用车车门建模标准,建立车门有限元模型,其中钣金件采用壳单元建模,车门 铰链采用实体单元建模,内板和外板之间的包边结构通过共节点模拟、粘胶采用六面体单元模拟,内 板和各加强板之间的焊点采用 CWLD 单元模拟。模型中用到的材料属性如表 1 所示。
表 1 车门有限元模型中的材料属性
| 材料 | 弹性模量 E(MPa) | 泊松比 μ | 密度 ρ(t/mm3) |
| 钢 | 210000 | 0.3 | 7.85e-9 |
| 粘胶 | 5 | 0.45 | 1.20e-9 |
3.2 车门焊点优化约束条件确定
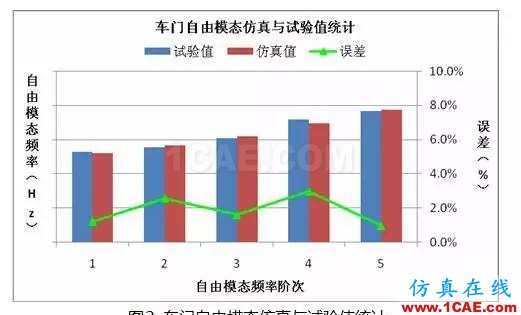
完整的车门结构性能分析包括模态分析、整体刚度分析、局部刚度分析、强度分析等 20 多项分 析内容,若将所有的分析项目都作为焊点优化的约束条件,计算成本高且不易实现。最终结合工程经 验确定了车门的自由模态(前三阶模态频率)、整体刚度(3 项)和局部刚度(1 项)作为焊点优化的 约束条件。在车门焊点优化模型建立之前,需要对上述分析项目进行预分析,以确定约束条件的具体 目标值。约束条件的设置如表 2 所示。
表 2 车门焊点优化模型约束条件
| 约束条件分析项目 | 原方案分析值 | 约束条件设定值 | |
|
自由 模态 |
一阶模态频率 | 44.7Hz | 大于 44Hz |
| 二阶模态频率 | 53.1Hz | 大于 52.5Hz | |
| 三阶模态频率 | 58.7Hz | 大于 58Hz | |
|
整体 刚度 |
门框刚度变形量 | 4.49mm | 小于 4.6mm |
| 弯曲刚度变形量 | -3.64mm | 大于-3.8mm | |
| 扭转刚度变形量 | -7.73mm | 大于-7.9mm | |
|
局部 刚度 |
窗台刚度变形量 |
-0.66mm |
大于-0.75mm |
3.3 车门焊点优化模型建立
优化设计有三要素,即设计变量、目标函数和约束条件。设计变量是在优化过程中发生改变而提 高性能的一组参数;目标函数是指要求的最佳设计性能,是关于设计变量的函数;约束条件是对优化 设计的限制,是对设计变量和其它性能的要求。确定了优化模型的约束条件后,根据本文的优化目的, 将 CWELD 焊点单元的密度作为设计变量,焊点单元的体积最小作为目标函数。设置完拓扑优化相关 的控制参数后,车门焊点优化模型可以进行求解计算。如果在求解过程中出现不收敛的情况,则需要 对约束条件进行调整。
4 车门焊点优化结果
4.1 车门焊点优化迭代过程
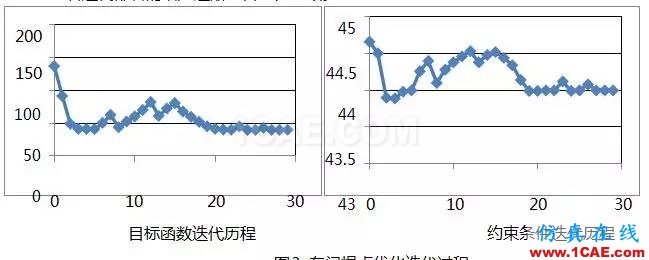
OptiStruct 经过 29 次迭代后最终得到焊点空间的优化结果。相应的约束条件的变化历程以及目标函数随迭代次数的变化关系如图 3 所示(图中仅示例列出一阶模态频率约束条件随迭代步数的变化历 程)。由图可知,整个迭代过程是向优化目标函数收敛的。焊点单元的体积随着迭代步数的增加不断 减少,约束条件也随着迭代部署的增加逐渐向目标值收敛。
4.2 车门焊点优化结果
车门结构拓扑优化后焊点分布如表 3 所示,其中密度区间为 0~0.1 中的 16 个焊点为可优化的焊 点。由于在建立优化模型时未将所有的结构性能分析项目作为约束条件,且约束条件的目标值较原方 案有所放宽,因此需要对优化结果结合工程经验进一步取舍。需注意的是,真实的一个三层焊点在模 型中表现为两个 CWELD 单元,故三层焊点的去留需综合考察两个设计单元的优化结果。
表 3 焊点密度分布表
|
焊点密度 |
0~0.1 |
0.1~0.2 |
大于 0.2 |
| 焊点数量 | 16 | 14 | 89 |
优化结果中密度区间为 0~0.1 中的 16 个焊点在车门结构中的分布如图 4 所示,将 16 个焊点划分为四个区域,每个区域中的焊点都需要经过进一步判断进行取舍。区域一中的 1 个焊点与周围焊点 间距较近,判断为冗余焊点,可直接删除。区域二中的 4 个焊点由于连接车门防撞杆与车门内板,且 靠近车门铰链附近,对车门强度和开闭耐久性能影响较大,需要全部保留。区域三中的 5 个焊点通过 稀疏排布减少 2 个焊点。区域四中的 6 个焊点通过更改焊点位置将两个焊点合并为一个焊点,可删除3 个焊点。通过对上述四个区域中的焊点判断取舍,共计可删除 6 个焊点,约占焊点总数的 5%,需 要对焊点优化后的车门结构性能进行全面校核。
4.3 焊点优化前后车门性能分析验证
对优化前后车门的模态、刚度、强度等性能进行对比分析,主要分析结果对比如表 4 所示。由表 中结果可知,焊点优化后,结构性能变化最大的是窗户的横向刚度,降低约 0.77% ,车门的主要结 构性能基本保持不变,焊点优化方案可行。
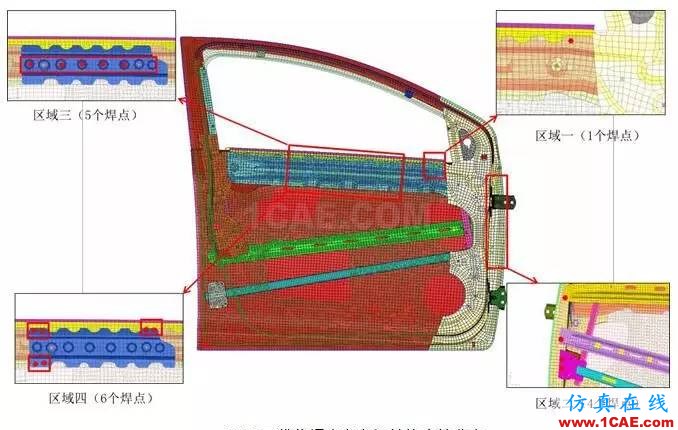
表 4 车门焊点优化前后结构性能对比
| 结构性能 | 原方案 | 优化方案 | 变化率 | |
|
模态 |
一阶模态频率 | 44.66Hz | 44.68Hz | 0.04% |
| 二阶模态频率 | 53.09Hz | 53.08Hz | 0.02% | |
| 三阶模态频率 | 58.71Hz | 58.71Hz | 0% | |
|
刚度 |
门框刚度变形量 | 4.498mm | 4.499mm | 0.02% |
| 弯曲刚度变形量 | -3.637mm | -3.639mm | 0.05% | |
| 扭转刚度变形量 | -7.728mm | -7.729mm | 0.01% | |
| 窗台刚度变形量 | -0.6596mm | -0.6647mm | 0.77% | |
| 下沉刚度变形量 | -7.726mm | -7.726mm | 0% | |
| 抗凹性能变形量 | 2.273mm | 2.275mm | 0.09% | |
| 风载变形变形量 | -0.9538mm | -0.9541mm | 0.03% | |
| 密封力变形变形量 | -0.7229mm | -0.7229mm | 0% | |
| 强度 | 过开强度塑性应变 | 1.863% | 1.863% | 0% |
| …… | …… | …… |
|
|
5 结束
(1)本文应用 HyperWorks/OptiStruct 对车门焊点进行拓扑优化设计,在车门结构性能基本保持 不变的情况下,发现冗余设计的焊点,单个车门减少了 6 个焊点,降低了生产制造成本。
(2)软件优化结果要结合焊接工艺、工程经验等因素进行判断取舍,方可获得切实可行的焊点 优化方案。
(3)本文仅针对已经布置完成的车门焊点进行拓扑优化设计,减少了焊点数量。若在设计初期 将焊点的数量,空间位置等参数化,通过优化工具实现焊点的合理分布,则可取得更为理想的效果。
相关标签搜索:基于 OptiStruct 的车门焊点优化设计 Ansys有限元培训 Ansys workbench培训 ansys视频教程 ansys workbench教程 ansys APDL经典教程 ansys资料下载 ansys技术咨询 ansys基础知识 ansys代做 Fluent、CFX流体分析 HFSS电磁分析 Abaqus培训






