ansys蠕变1
2017-03-18 by:CAE仿真在线 来源:互联网
4.4 蠕变分析
4.4.1 蠕变理论
4.4.1.1 定义
蠕变是率相关材料非线性,即在常荷载作用下,材料连续变形的特性。相反如果位移固定,反力或应力将随时间而变小,这种特性有时也称为应力松驰,见 图4-18a 。
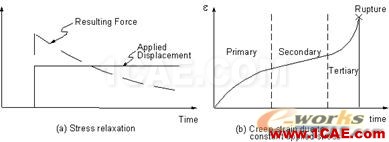
图4-18 应力松弛和蠕变
蠕变的三个阶段如 图4-18b 所示。在初始蠕变阶段,应变率随时间而减小,这个阶段一般发生在一个相当短的时期。在第二期蠕变阶段,有一个常应变率,所以应变以常速率发展,在第三期蠕变阶段,应变率迅速增加直到材料失效。
由于第三期蠕变阶段所经历的时间很短,材料将失效,所以通常情况下,我们感兴趣的是初始蠕变和第二期蠕变。ANSYS程序中的蠕变行为用来模拟初始蠕变和第二期蠕变。蠕变系数可以是应力、应变、温度、时间或其它变量的函数。
在高温应力分析中(如核反应堆等),蠕变分析非常重要。例如,假设在核反应堆中施加了预荷载,以保证与相邻部件保持接触而不松开。在高温下过了一段时间后,预荷载将降低(应力松驰),可能使接触部件松开。对于一些材料如预应力砼,蠕变也可能十分重要。最重要的是要记住,蠕变是永久变形。
4.4.1.2 理论介绍
蠕变方程:我们通过一个方程来模拟蠕变行为,此方程描述了在实验中观测到的主要特征(特别是在一维的拉伸实验中)。这个方程以蠕应变率的方式表示出来,其形式如下:
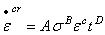
上式中,A、B、C、D是从实验中得到的材料常数,常数本身也可能是应力,应变,时间或温度的函数,这种形式的方程被称为状态方程。
上式中,当常数D为负值时,蠕应变率随时间下降,材料处于初始蠕变阶段,当D为0时,蠕应变率为常值,材料处于第二期蠕变阶段。
对于2-D或3-D应力状态,使用VON Mises方程计算蠕应变率方程中所使用的标量等效应力和等效应变。
对蠕变方程积分时,我们使用经过修改的总应变,其表达式为:
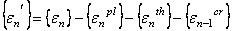
经过修改的等效总应变为:
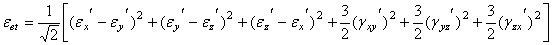
其等效应力由下式算出:

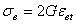
其中:G=剪切模量= 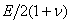
等效蠕应变增量 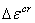 由程序给出的某一种公式进行计算,一般为正值,如果在数据表中
由程序给出的某一种公式进行计算,一般为正值,如果在数据表中 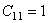 ,则使用的是衰减的蠕应变率而不是常蠕变率,但这个选项一般不被推荐,因为在初始蠕变所产生的应力为主的情况下,它可能会严重的低估蠕变值。如果
,则使用的是衰减的蠕应变率而不是常蠕变率,但这个选项一般不被推荐,因为在初始蠕变所产生的应力为主的情况下,它可能会严重的低估蠕变值。如果 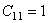 ,程序使用修正的等效蠕应变增量来代替蠕应变增量。
,程序使用修正的等效蠕应变增量来代替蠕应变增量。
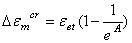
其中:e=2.718281828(自然对数的底数)
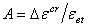
下面是计算积分点的蠕应变率与弹性应变比率的公式:
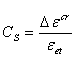
将本次迭代的所有单元的所有积分点的的最大值记为 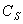 ,并且作为“CREEPRATIO”输出。
,并且作为“CREEPRATIO”输出。
计算出等效蠕应变增量后,可将它转换成分量的形式,假设 Nc 是某个特定单元类型的应变分量的个数。
如果 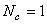 则有:
则有:
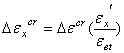
如果 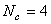 ,则有:
,则有:
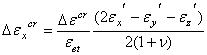
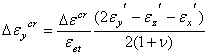
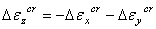
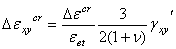
上式中,前三个为正应变分量,第四个是剪应变分量。
如果 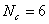 ,前四个分量与上式相同,另两个剪应变分量为:
,前四个分量与上式相同,另两个剪应变分量为:
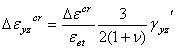
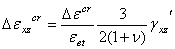
接下来,可以按下式来计算弹性应变和总的蠕应变(以 X 方向的分量为例):
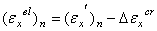
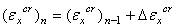
为了从标量 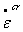 来计算分量
来计算分量 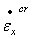 ,
, 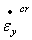 ,
, 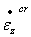 ,程序使用相关流动准则:Prandtl-Reuss方程,与塑性应变相同,蠕应变只有偏差分量(剪分量),没有由于蠕变引起的体积应变。
,程序使用相关流动准则:Prandtl-Reuss方程,与塑性应变相同,蠕应变只有偏差分量(剪分量),没有由于蠕变引起的体积应变。
为了考虑应力随时间的变化,使用两种强化准则,时间强化和应变强化。我们以一简单拉伸试验来说明:刚开始时,杆被加载到应力为 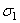 ,在时间
,在时间 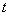 它被卸载到应力为
它被卸载到应力为 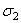 。
。
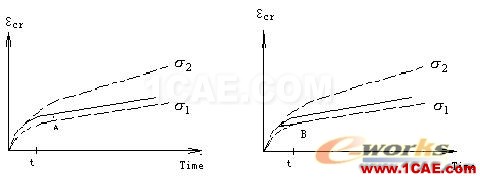
(a) 时间强化 (b) 应变强化
图4-19 典型的单轴蠕变曲线
时间强化假定蠕应变率仅仅依赖于蠕应变过程开始的时间。当应力从 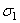 变到
变到 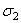 时,材料的蠕变率由点A表示(相当于曲线向上移动)。
时,材料的蠕变率由点A表示(相当于曲线向上移动)。
应变强化假定蠕应变率仅仅依赖于材料中的应变,当应力从 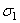 变到
变到 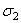 时,材料的蠕变率由点B表示(相当于曲线左移)。大多数实验数据与应变强化准则吻合得更好。
时,材料的蠕变率由点B表示(相当于曲线左移)。大多数实验数据与应变强化准则吻合得更好。
4.4.2 求解算法
ANSYS使用隐式和显式积分二种方法来进行蠕变分析,均可应用于静态和瞬态分析。隐式蠕变分析方法更强大、更快、更精确,一般推荐使用隐式蠕变分析。它可以处理温度相关蠕变常数,同时模拟蠕变与等向强化塑性模型。
对于需要很小时间步的情况,显式蠕变分析就非常有用。蠕变常数不能有温度相关性,而与其他塑性材料模型的耦合只能应用迭加法。
注意 --蠕变分析中的“隐式”和“显式”,与“显式动力分析”或“显式单元”没有任何关系。
隐式蠕变分析方法支持下列单元:PLANE42,SOLID45,PLANE82,SOLID92, SOLID95,LINK180,SHELL181,PLANE182,PLANE183,SOLID185,SOLID186,SOLID187,BEAM188 和 BEAM189。
显式蠕变分析方法支持下列单元:LINK1,PLANE2,LINK8,PIPE20,BEAM23, BEAM24,PLANE42,SHELL43,SOLID45,SHELL51,PIPE60,SOLID62,SOLID65,PLANE82,SOLID92 和 SOLID95。
蠕变应变率可以是应力、应变、温度、电子流水平的函数。蠕变应变率方程已按初始蠕变、第二期蠕变和辐射引起的蠕变在ANSYS中建立。参见《ANSYS Elements Reference》中关于这些蠕变方程的讨论和输入方法。有一些方程需要特殊的单位。特别是,对于显式蠕变选项,蠕变方程中的温度应当基于绝对温度。
4.4.2.1 隐式蠕变方法
隐式蠕变方法的基本步骤包括应用 TB 命令( Lab =CREEP),通过 TBOPT 值选择蠕变方程。TBOPT的输入值对应于特定的蠕变方程, ANSYS程序所提供的隐式蠕变方程如下:
· TBOPT=1 所对应的蠕变方程(初始蠕变方程):
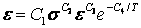
· TBOPT=2 所对应的蠕变方程(初始蠕变方程):
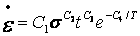
· TBOPT=3 所对应的蠕变方程(初始蠕变方程):
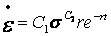 ,
, 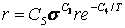
· TBOPT=4 所对应的蠕变方程(初始蠕变方程):
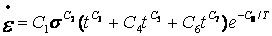
· TBOPT=5 所对应的蠕变方程(初始蠕变方程):
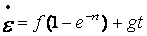
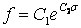 ,
, 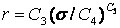 ,
, 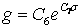
· TBOPT=6 所对应的蠕变方程(初始蠕变方程):
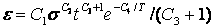
· TBOPT=7 所对应的蠕变方程(初始蠕变方程):
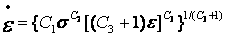
· TBOPT=8 所对应的蠕变方程(初始蠕变方程):
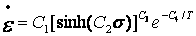
· TBOPT=9 所对应的蠕变方程(二期蠕变方程):
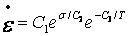
· TBOPT=10 所对应的蠕变方程(二期蠕变方程):
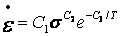
· TBOPT=11 所对应的蠕变方程(初始蠕变+二期蠕变方程):
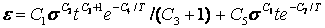
· TBOPT=12 所对应的蠕变方程(初始蠕变+二期蠕变方程):
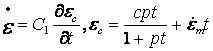

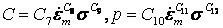
· TBOPT=100 所对应的蠕变方程:
用户自定义的蠕变方程
在以上方程中:
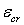 =等效蠕应变
=等效蠕应变
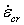 =等效蠕应变对时间的变化率
=等效蠕应变对时间的变化率
 =等效应力
=等效应力
T=绝对温度, 程序内部温度偏移量(TOFFST)被加到所有的温 度上。
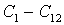 =通过TBDADA命令所输入的材料常数
=通过TBDADA命令所输入的材料常数
t=子步的结束时间。
下例说明隐式蠕变分析方法。 TBOPT =2表示将应用初始蠕变方程于模型2。温度相关性通过 TBTEMP 命令来指定,与此方程有关的4个常数作为 TBDATA 命令的参数。
TB,CREEP,1,1,4,2
TBTEMP,100
TBDATA,1,C1,C2,C3,C4
用户也可以应用ANSYS的可编程特性,并设置 TBOPT =100 来输入其他蠕变表达式。可以用 TB 命令( Lab =STATE)来定义状态变量数。下例是如何定义5个状态变量的例子:
TB,STATE,1,,5
用户可以同时模拟蠕变[ TB, CREEP]和各向同性强化、双线性随动强化和HILL各向异性塑性来考察更复杂的材料行为。参阅《ANSYS Element Reference》中的《Material Model Combination》部分来了解可用的联合使用。另外参阅本书§4.6《Material Model Combination》中材料联合使用的输入命令。
为了执行隐式蠕变分析,用户必须应用求解 RATE 命令( Option =ON或1)。下面的例子说明一个时间强化蠕变分析,见 图4-20 。

图4-20 时间强化蠕变分析
用户在第1荷载步施加机械荷载,并把 RATE 命令设为 OFF,这样绕过(忽略)蠕变应变效应。由于在这一荷值步的时间间隔将影响其后的总时间,因此这一荷载步的时间间隔要充分小。例如,用户可指定时间值为1E-8秒。第2荷载步是蠕变分析。这时应把 RATE 命令设为ON。这里机械荷载保持为常数,而材料随时间增量而发生蠕变。
/SOLU !First load step, apply mechanical loading
RATE,OFF !Creep analysis turned off
TIME,1.0E-8 !Time period set to a very small value
...
SOLV !Solve this load step
!Second load step, no further mechanical load
RATE,ON !Creep analysis turned on
TIME,100 !Time period set to desired value
...
SOLV !Solve this load step
RATE命令仅对采用von Mises 和Hill势的隐式蠕变有效。
当采用von Mises势模拟隐式蠕变时,可以对如下单元运用RATE命令:LINK180, SHELL181, PLANE182, PLANE183, SOLID185, SOLID186, SOLID187, BEAM88, BEAM189。
当模拟各向异性蠕变时( TB , CREEP 和 TB , HILL),可以对如下单元运用RATE命令:PLANE42, SOLID45, PLANE82, SOLID92, SOLID95, LINK180, SHELL181, PLANE182, PLANE183, SOLID185, SOLID186, SOLID187, BEAM88, BEAM189。
对于大多数材料,在早期阶段,蠕变应变率显著改变。因为这一原因,通常建议应用很小的初始时间步增量,然后应用求解命令 DELTIM 或 NSUBST 指定较大的最大增量时间步。对于隐式蠕变,用户可能需要在结果中仔细检验时间增量的影响,因为ANSYS缺省并不提供任何蠕变率的控制。用户可以应用 CRPLIM 或 CUTCONTROL ,CRPLIMIT 命令中的蠕变率控制选项来总是强迫采用一个蠕变极限比率。蠕变极限比率的推荐值是1~10。该比率可以随材料而变化,以便用户可以根据自己的经验来决定一个最佳值,从而获得需要的运行和精度。对于大型分析,建议首先在一个小模型中对时间增量收敛分析进行测试。
4.4.2.2 显式蠕变方法
显式蠕变方法求解蠕应变使用了欧拉朝前法,以时间步开始时的应力、应变为基础计算出蠕应变率,在每个时间步长内,蠕应变率被假定是常数,因此有:
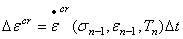
使用这种方法所对应的蠕应变曲线如下:

图4-21 显式蠕变对应的蠕应变曲线
为了减小误差,需要小的时间步长,特别是在蠕应变率变化很大的区域。
蠕应变率越小,结果越精确。一个等于或小于0.1的蠕变率将产生相当精确的结果。如果步长太大,求解将变得不稳定,并且不收敛,稳定极限对应于0.25的蠕应变率。
对于在第二期蠕变阶段蠕变较小的情况,欧拉朝前法是一种十分有效的方法,对于蠕应变较大的情况,这种方法需要时间步长很小,对于高度非线性蠕变应变-时间曲线,在应用显式蠕变方法时,必须应用小的时间步。如果时间步小于1E-6,则不计算蠕变应变。若需自动调整时间步到合适的值,可以应用蠕变时间步优化选项[ AUTOTS 和 CRPLIM ]。
如果没有其它的非线性行为则:
l 只在每一个子步的开始修正蠕应变率,在此子步内将不再变化。
l 不执行牛顿-拉普森迭代,因此,求解精度依赖于时间步长。
如果有其它的非线性行为则有:
l 既然蠕应变影响应力分布(反过来应力分布又影响蠕变率),因此在每个时间步内都要进行牛顿-拉普森迭代
l 缺省情况下,使用初始刚度的牛顿-拉普森选项(总是使用弹性刚度矩阵)。
l 既然时间步长很小,使用切线矩阵并不能使求解过程更有效。
显式蠕变方法的基本步骤,包括应用 TB 命令( Lab =CREEP),选择蠕变方程(用 TBDATA 命令的参数加入适当的常数)。 TBOPT 为0或者为空白。下例是应用显式蠕变方法的输入。请注意,所有常数是作为 TBDATA 命令的参数加入的,而且无温度相关性。
TB,CREEP,1
TBDATA,1,C1,C2,C3,C4, ,C6
ANSYS程序中具有一个蠕变方程库供你选择,你可以根据材料特性选择相应的蠕变准则,也就是说,在ANSYS程序中,建立了某些特定材料的特定蠕变准则,特别是那些用于原子能工业方面的材料(例如304和316不锈钢,2 1/4 Cr-1锰低铝钢),另外,用户还可以建立自己的蠕变准则,应用程序的可编程特性加入用户蠕变表达式,见《ANSYS Guide to User Programmable Fealares》。
可通过数据表来输入蠕变材料常数:
Main Menu: Preprocessor>Material Props>Material Models
通过输入 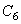 的值进入到初始蠕变的计算,如果
的值进入到初始蠕变的计算,如果 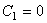 将略过蠕变计算。通过输入
将略过蠕变计算。通过输入 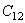 的值进入到第二期蠕变阶段的计算,如果
的值进入到第二期蠕变阶段的计算,如果 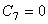 将略过此阶段的计算,如果使用选项
将略过此阶段的计算,如果使用选项 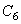 =9、10、11、13、14或15来进行初始蠕变的计算,由于在它们的公式中包括了第二期蠕变的计算,故第二期蠕变的计算被略过,通过输入
=9、10、11、13、14或15来进行初始蠕变的计算,由于在它们的公式中包括了第二期蠕变的计算,故第二期蠕变的计算被略过,通过输入 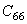 的值进入到辐射引起的蠕变计算,通过输入
的值进入到辐射引起的蠕变计算,通过输入 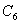 =100,进入到用户自己定义蠕变准则的计算。下面我们详细说明一下ANSYS程序所提供的蠕变准则。
=100,进入到用户自己定义蠕变准则的计算。下面我们详细说明一下ANSYS程序所提供的蠕变准则。
· 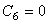 时的初始蠕变方程。
时的初始蠕变方程。
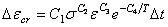
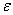 =等效应变(以修改的总应变为基础)
=等效应变(以修改的总应变为基础)
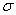 =等效应力
=等效应力
T=绝对温度(所有给定温度加上TOFFST)
t=在子步结束的时间
e=自然对数的底数
· 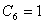 时的初始蠕变方程
时的初始蠕变方程
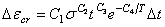
· 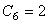 时的初始蠕变方程。
时的初始蠕变方程。
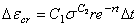
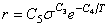
· 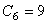 的初始蠕变方程, 适用于退火304不锈钢:
的初始蠕变方程, 适用于退火304不锈钢:
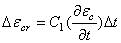
可以使用几种不同的蠕变方程来计算 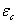
双指数蠕变方程 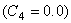
为了使用下面的双指数蠕变方程来计算 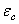 ,输入
,输入 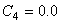
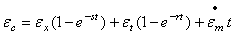
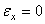
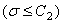
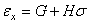
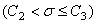
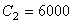 Psi(缺省)
Psi(缺省) 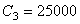 Psi(缺省)
Psi(缺省)
S,r, 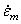 ,G和H是温度和应力的函数。
,G和H是温度和应力的函数。
对于退火304不锈钢,当温度在800 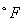 -1100
-1100 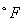 时,上面的双指数方程是有效的,上式中的前两项描述了初始蠕变,最后一项描述了第二期蠕变。
时,上面的双指数方程是有效的,上式中的前两项描述了初始蠕变,最后一项描述了第二期蠕变。
为了使用这个方程,输入一个非零的 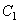 值,
值, 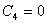 ,
, 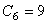 ,
, 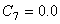 。温度应该使用
。温度应该使用 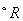 (或
(或 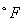 且TOFFST=460.0),如果温度低于有效范围,则不计算蠕变,时间以小时为单位,应力使用Psi,有效的应力范围为6000-25000Psi。
且TOFFST=460.0),如果温度低于有效范围,则不计算蠕变,时间以小时为单位,应力使用Psi,有效的应力范围为6000-25000Psi。
使用公制单位的标准有理多项式蠕变方程( 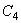 =1)
=1)
为了使用公制单位的标准有理多项式蠕变方程来计算 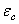 ,输入
,输入 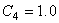
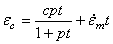
c=初始蠕应变的几极值
p=初始蠕变的时间因子
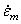 =第二期蠕变阶段的蠕变率(最小蠕变率)
=第二期蠕变阶段的蠕变率(最小蠕变率)
对于退火的304不锈钢,当温度在427 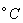 -704
-704 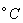 时,上面的标准有理多项式蠕变方程是有效的,上式中第一项描述了初始蠕变,最后一项描述了第二期蠕变。
时,上面的标准有理多项式蠕变方程是有效的,上式中第一项描述了初始蠕变,最后一项描述了第二期蠕变。
为了使用上面的方程,输入 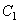 =1.0,
=1.0, 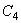 =1.0,
=1.0, 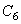 =9.0和
=9.0和 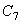 =0.0,温度必须用
=0.0,温度必须用 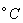 为单位(TOFFST=273),如果温度低于有效范围,则不计算蠕变,时间以小时为单位,应力用Mpa。
为单位(TOFFST=273),如果温度低于有效范围,则不计算蠕变,时间以小时为单位,应力用Mpa。
通过选择 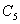 的值来控制蠕变的强化准则,
的值来控制蠕变的强化准则, 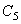 =0.0,选择时间强化.
=0.0,选择时间强化. 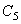 =1.0选择总的蠕应变强化,
=1.0选择总的蠕应变强化, 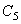 =2.0选择初始蠕变强化。
=2.0选择初始蠕变强化。
使用英制单位的有理多项式蠕变方程( 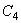 =2.0)
=2.0)
为了在英制单位下使用上面的标准有理多项式蠕变方程,输入 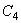 =2.0。此时温度应以
=2.0。此时温度应以 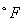 为单位(TOFFST=460),应力为PSI,有效温度范围为800-1300
为单位(TOFFST=460),应力为PSI,有效温度范围为800-1300 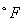 。
。
· 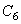 =10的初始蠕变方程。 适用于退火316不锈钢:
=10的初始蠕变方程。 适用于退火316不锈钢:
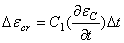
与退火304不锈钢相同,也可以使用几种不同的蠕变方程来计算 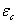 。
。
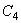 =0时的双指数蠕变方程。
=0时的双指数蠕变方程。
使用与退火的304不钢相同的双指数蠕变方程( 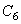 =9.0,
=9.0, 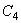 =0.0),与退火304不锈钢所用方程不同的是有效应力范围为4000-30000PSI,
=0.0),与退火304不锈钢所用方程不同的是有效应力范围为4000-30000PSI, 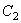 缺省为4000PSI,
缺省为4000PSI, 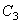 缺省为30000PSI。
缺省为30000PSI。
使用公制单位的标准有理多项式蠕变方程( 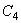 =1.0)
=1.0)
与 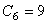 所描述的退火304不锈钢所用的标准有理多项式蠕变方程(
所描述的退火304不锈钢所用的标准有理多项式蠕变方程( 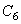 =9.0,
=9.0, 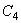 =1.0)相同。不同的是:其有效温度范围是482-704
=1.0)相同。不同的是:其有效温度范围是482-704 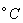 。
。
使用英制单位的有理多项式蠕变方程( 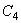 =2.0)
=2.0)
与 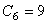 所描述的相同,所不同的是:温度必须以F为单位,TOFFST=460,应力以PSI为单位,且有效范围为0.0-24220PSI,温度范围为900-1300
所描述的相同,所不同的是:温度必须以F为单位,TOFFST=460,应力以PSI为单位,且有效范围为0.0-24220PSI,温度范围为900-1300 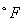 。
。
· 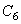 =11的初始蠕变方程。
=11的初始蠕变方程。
适用于退火2 1/4 Cr-1 Mo 低合金钢
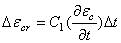
可以使用几种不同的蠕变方程来计算 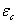 。
。
修改的有理多项式蠕变方程( 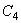 =0.0)
=0.0)
为了使用下面修改的有理多项式蠕变方程来计算 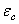 ,需输入
,需输入 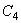 =0.0:
=0.0:
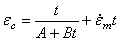
A、B、 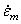 是温度和应力的函数。
是温度和应力的函数。
对2 1/4 Cr-1 Mo低合含钢,当温度在700-1100 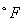 范围内时,修改的有理多项式方程是有效的,第一项描述了初始蠕变,第二项描述了第二期蠕变。
范围内时,修改的有理多项式方程是有效的,第一项描述了初始蠕变,第二项描述了第二期蠕变。
为了使用上式须输入 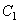 =1.0,
=1.0, 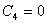 ,
, 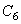 =11.0和
=11.0和 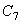 =0.0温度必须以
=0.0温度必须以 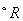 为单位(或以
为单位(或以 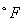 为单位且TOFFST=460.0),时间以小时为单位,应力以PSI为单位,有效应力范围是1000-65000PSI。
为单位且TOFFST=460.0),时间以小时为单位,应力以PSI为单位,有效应力范围是1000-65000PSI。
公制单位的标准有理多项式蠕变方程( 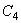 =1.0)
=1.0)
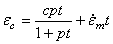
c=初始蠕应变的极值
p=初始蠕变时间因子
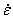 =第二期蠕变阶段的蠕应变率
=第二期蠕变阶段的蠕应变率
对退火的2 1/4 Cr-1 Mo 低合金钢,当温度371 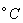 -593
-593 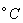 ,上式是有效的。
,上式是有效的。
为了使用上式,输入 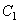 =1.0,
=1.0, 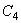 =1.0,
=1.0, 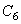 =11.0和
=11.0和 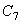 =0.0。温度以
=0.0。温度以 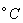 为单位,TOFFST=273。时间用小时为单位,应力为Mpa,强化准则与
为单位,TOFFST=273。时间用小时为单位,应力为Mpa,强化准则与 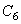 =9.0所使用的相同。
=9.0所使用的相同。
英制单位的有理多项式蠕变方程( 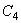 =2.0)
=2.0)
与标准有理多项式蠕变方程相同,除了温度以 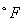 为单位,TOFFST=460,应力为PSI,有效温度范围为700-1100
为单位,TOFFST=460,应力为PSI,有效温度范围为700-1100 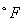 。
。
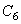 =12的初始蠕变方程
=12的初始蠕变方程
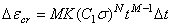
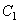 =比例常数
=比例常数
M、N、K=温度函数
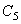 :描述M、N、K函数的温度值的个数
:描述M、N、K函数的温度值的个数
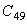 :第一个绝对温度值
:第一个绝对温度值
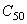 :第二个绝对温度值
:第二个绝对温度值
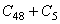 :第
:第 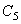 个绝对温度的值
个绝对温度的值
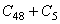 +1:第一个M的值
+1:第一个M的值
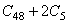 :第
:第 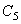 个M的值
个M的值
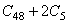 +1:第一个N的值
+1:第一个N的值
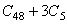 :第
:第 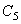 个N的值
个N的值
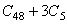 +1:第一个K的值
+1:第一个K的值
??
系数随温度而变的幂函数蠕变准则与 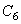 =1的方程相似,但
=1的方程相似,但 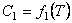 ,
, 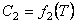 ,
, 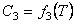 ,
, 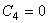 。温度必须以降序输入。
。温度必须以降序输入。
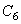 =13的初始蠕变方程
=13的初始蠕变方程
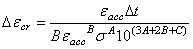
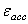 =积累的蠕应变
=积累的蠕应变
A= 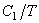
B= 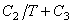
C= 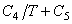
常数 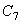 应该输入0,
应该输入0, 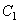 不应该输入0。
不应该输入0。
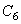 =14的初始蠕变方程
=14的初始蠕变方程
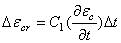
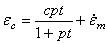
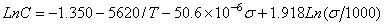
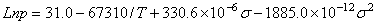
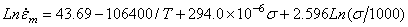
对于退火的316不锈钢,当温度为800 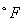 -1300
-1300 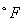 ,上面的蠕变方程有效。为了使用上式,输入
,上面的蠕变方程有效。为了使用上式,输入 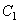 =1.0和
=1.0和 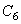 =14.0。温度采用
=14.0。温度采用 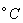 (或用
(或用 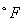 且TOFFST=460,时间以小时为单位,常数仅适用于英制单位,应力范围为0.0-45000PSI。
且TOFFST=460,时间以小时为单位,常数仅适用于英制单位,应力范围为0.0-45000PSI。
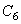 =15 的初始蠕变方程。
=15 的初始蠕变方程。
一般材料的有理多项式蠕变方程:
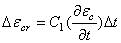
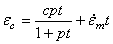
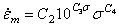
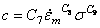
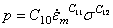
上面的有理多项式蠕变方程是标准有理多项式蠕变方程 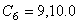 和11.0(
和11.0( 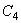 =1.0和2.0的一般形式,对于等温情况,此方程变为标准方程,强化准则与
=1.0和2.0的一般形式,对于等温情况,此方程变为标准方程,强化准则与 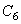 =9.0的情况相同。
=9.0的情况相同。
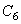 =100的标准蠕变方程。
=100的标准蠕变方程。
通过输入 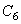 =100建立用户自已定义的蠕变方程。
=100建立用户自已定义的蠕变方程。
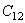 =0的第二期蠕变方程
=0的第二期蠕变方程
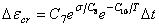
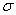 =等效应力
=等效应力
T=绝对温度
t=时间
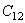 =1的等二期蠕变方程
=1的等二期蠕变方程
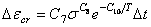
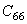 =5的由辐射引起的蠕变方程
=5的由辐射引起的蠕变方程
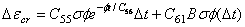
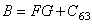
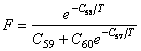
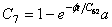
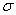 =等效应力
=等效应力
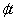 =中子通量
=中子通量
对于冷加工的316不锈钢,当温度在700-1300 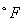 时,上式有效。
时,上式有效。
4.4.3 蠕变分析实例
4.4.3.1 问题描述
一块矩形板,其左端固定,而右端被拉伸至某一固定位置,然后保持在此位置不动。试分析板中应力随时间的变化。
4.4.3.2 问题详细说明
材料特性:
Ex=2e5
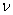 (泊松比)=0.3
(泊松比)=0.3
C6=0的显式初始蠕变方程:
C1=4.8e-23
C2=7
几何特性:
L=100
H=10

图4-22 问题描述图
4.4.3.3 求解步骤(GUI方法)
步骤一:建立计算所需要的模型
在这一步中,建立计算分析所需要的模型,包括定义单元类型,创建结点和单元,并将数据库保存为“creep.db”,在此对这一过程不再详细。
步骤二:恢复数据库文件 “ creep.db ”
utility menu>file>Resume from
步骤三:定义材料性质
1、选“Main Menu>Preprocessor>Material Props>Material Models”。出现“Define Material Model Behavior”对话框,选择Material Model Number 1。
2、在“Material Models Available”窗口,双击“Structural->Linear->Elastic-> Isotropic”。出现一个对话框。
3、对杨氏模量(EX)键入2e5 。
4、对泊松比(NUXY)键入0.3。
5、单击OK。
步骤四:定义creep数据表并输入相应值
1、在“Material Models Available”窗口,双击Structural->Nonlinear->Inelastic->Rate Dependent->Creep->Creep Only->Mises Potential->Explicit,出现一个对话框。
2、在对话框表格中的C1,C2位置输入相应值(C1=4.8e-23,C2=7)。
3、单击OK
4、退出“Define Material Model Behavior”对话框。
步骤五:进入求解器
选择菜单路径Main Menu>Solution
步骤六:加载
根据所给条件,施加适当的约束和载荷。在此不作详述,参考命令流文件。
步骤七:定义分析类型:
1、选择菜单路径Main Menu>Solution>-Analysis Type-New Analysis.
2、单击“Static”来选中它然后单击OK。
步骤八:设置输出控制选项
1、选择菜单路径:Main Menu >Solution>Unabridged Menu >Load step opts-Output ctrls> Solu printout。对话框出现
2、在“Item”中,选择“all items”
3、对“FREQ”,选择“Every Substep”
4、单击OK
5、选择菜单路径:Main Menu > Solution>Unabridged Menu >Load step opts-Output ctrls > DB/Results File。对话框出现。
6、在“Item”中,选择“all items”
7、对“FREQ”,选择“Every Substep”
8、单击OK
步骤九:设置载荷步选项
1、选择菜单路径Main Menu> Solution>Unabridged Menu>Load step opts-Time/Frequenc> Time and substps。对话框出现。
6、对“Time”(载荷步终止时间)键入10000
7、对“NSUBST”(子步数) 输入100
8、将“KBC”(加载方式)设置为Stepped
步骤十:进行求解
步骤十一:进行后处理
4.4.3.4 求解步骤(命令流方法)
fini
/cle
l=100
h=30
n1=10
n2=3
/prep7
et,1,42
rect,0,l,0,h
lsel,s,loc,y,0
lesize,all,,,n1
lsel,s,loc,x,0
lesize,all,,,n2
mshkey,1
mshape,0,2d
amesh,all
save,creep,db
resume,creep,db
mp,ex,1,2e5
mp,prxy,0.3
TB,CREEP,1
TBDATA,1,4.8E-23,7 ! CREEP PROPERTIES
/solu
nsel,s,loc,x,0
d,all,all
nsel,s,loc,x,l
d,all,ux,0.1
alls
BFUNIF,TEMP,900 ! UNIFORM TEMPERATURE
TIME,10000
KBC,1
NSUBST,100
OUTPR,all,all
OUTRES,all,all
alls
SOLVE
fini
相关标签搜索:ansys蠕变1 Ansys有限元培训 Ansys workbench培训 ansys视频教程 ansys workbench教程 ansys APDL经典教程 ansys资料下载 ansys技术咨询 ansys基础知识 ansys代做 Fluent、CFX流体分析 HFSS电磁分析 Abaqus培训






