基于ANSYS的支架稳定性分析
2017-03-30 by:CAE仿真在线 来源:互联网
随着大跨度桥梁在我国西南大山大河地区的高速发展,超高的桥梁支架在工程建设中的应用也日益广泛,这种细长结构的稳定性问题与强度问题同样重要,有时甚至起控制作用,因此对此类支架进行稳定性分析是十分必要的。
本文利用有限元分析软件 ANSYS 建立了扣件式钢管支架的计算模
型,通过对比不同支撑搭设方式下支架的极限承载力,对扣件式支架结构体系中支撑的作用进行了分析。主要内容有:
1.在 ANSYS 有限元软件中建立分析支架结构的合理模型,并验证模型的正确性。
2.利用所建立的有限元模型,分析此类支架结构体系的失稳形式和其中支撑的作用。
一般地,可以把建筑物的生命周期分为三个阶段施工建造阶段、正常使用阶段和维修加固阶段。研究人员及设计工程师把大量的努力用在如何保障建筑物在正常使用阶段安全可靠的工作上。虽然施工建造阶段存在大量的未知不定性,但在该方面的研究工作却相对较少。对于一般性建筑物来说,建造时间一般为一到两年,其使用寿命大致为五十年左右,然而,据统计。事故绝大多数发生在建筑施工阶段,其中桥梁支架、模板架这些临时辅助施工设施的坍塌是事故发生的主要原因。可见,对施工过程中桥梁支架体系的研究是一项必要、迫切和重要的工作。
钢管支架大致可分为固定式组合支架、移动式支架和吊支架三大类, 其中固定式组合支架又包括钢管支架和框式支架两大类。本文主要介绍的扣件式钢管支架由钢管和扣件组成、具有加工简便、搬运方便、通用性强等特点,已成为当前我国使用量最大、应用最普遍的一种支架,占支架使用总量的左右,在今后较长时间内,这种支架仍占主导地位。但是, 这种支架的安全保证性较差,施工工效低,不能满足高层建筑施工的发展需要。
在钢管支架不断完善和发展的同时,桥梁支架以其施工简便快捷、整体性好等特点而得到广泛的应用于桥梁施工过程中,但同时也伴随着一个日趋突出的问题一支架倒塌问题,近年来,一些地区多次发生施工过程中钢管支架倒塌的重大工程事故,造成人员和财产的巨大损失,产生了恶劣的社会影响,因此,有必要对桥梁支架进行进一步的深入研究。
牛津大学编制了计算脚手架稳定特征值程序且有不少国家已在不同程度上规定了考虑材料进入弹塑性的方法,同时也考虑了初始缺陷及风荷载的影响。日本曾对门式钢管脚手架结构进行了试验分析,并编制了安全技术规程。他们主要从单跨入手,对单层,2层,3层,5层进行了试验分析,得到了基本的压屈形态及极限承载力,同时还给出了计算单榀门架压屈承载力的方法。
英国的Godley比较了二维模型和三维模型对计算脚手架刚度的影响程度,指出节点半刚性的考虑对脚手架动力特性研究的重要性。后来,Godley在计算脚手架系统时进行了二阶几何非线性分析并考虑使用节点非线性模型。 美国的Weesner和Jones对四种不同形式的高度为5米的承重脚手架进行了极限承载力试验研究并与利用有限元软件ANSYS得到的脚手架特征值屈曲荷载和几何非线性分析结果加以分析对比,认为几何非线性分析得到的极限承载力数值低于特征值屈曲荷载,但与试验数值相近。
1989年,哈尔滨建筑工程学院徐崇宝教授等对双排扣件式钢管脚手架工作性能进行了理论分析和试验研究。
2007年,北京交通大学硕士研究生王勇对超高扣件式钢管模板支架安全性进行了分析。
2007年,浙江大学硕士研究生胡凯山对扣件式钢管模板支撑架结构力学性能进行了研究。
2009年,天津大学和《建筑施工扣件式钢管脚手架安全技术规范》的编制组对扣件式钢管支架结构进行了一系列试验研究工作,给出了试验模型的极限承载力。
屈曲分析是一种用于确定结构开始变的不稳定时的临界荷载和屈曲模态形状(结构发生屈曲响应时的特征形状)的技术。ANSYS提供了两种结构屈曲荷载和屈曲模态的分析方法:非线性屈曲分析和特征值(线性)屈曲分析,这两种方法通常得到不同的结果。非线性屈曲分析比线性屈曲分析更精确,故常用于对实际结构的设计或计算。该方法用一种逐渐增加载荷的非线性静力分析技术来求得使结构开始变得不稳定时的临界载荷(图2-1a)。应用非线性技术,模型中就可以包括诸如初始缺陷、塑性、间隙、大变形响应等特征。此外,使用偏离控制加载,还可以跟踪结构的后屈曲行为。特征值屈曲分析用于预测一个理想弹性结构的理论屈曲强度(分叉点)(图2-1b)。该方法相当于弹性屈曲分析方法。例如,一个柱体结构的特征值屈曲分析的结果,将与经典欧拉解相当。但是,初始缺陷和非线性使得很多实际结构都不是在其理论弹性屈曲强度处发生屈曲。
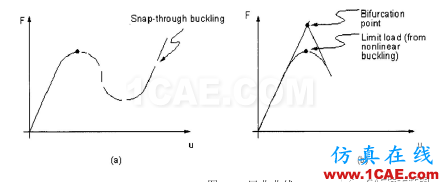
因此,特征值屈曲分析经常得出非保守结果,通常不能用于实际的工程分析。
特征值屈曲按如下步骤进行分析:1、建立模型;2、获得静力解;3、获得特征值屈曲解;4、展开解;5、观察结果。
1)建立模型
定义作业名和分析标题,使用前处理器定义单元类型、单元实常数、材料性质、模型几何实体。建模过程中应注意:只允许线性行为,如果定义了非线性单元,则将按线性单元对待;必须定义材料的弹性模量 EX。材料性质可以是线性、各向同性或各向异性,恒值或与温度相关。
2)获得静力解
该过程与一般静力分析过程一致,但要注意:必须激活预应力影响[PSTRES],因为该分析需要计算应力刚度矩阵;通常只要施加一个单位载荷就足够了。由屈曲分析计算出的特征值,表示屈曲载荷系数。因此,若施加的是单位载荷,则该特征值就表示实际的屈曲载荷。
3)获得特征值屈曲解
步骤为:1.进入 ANSYS 求解器;2.定义分析类型和分析选项;3.定义荷载步选项;4.开始求解;5.退出求解器。
4)展开解
要观察屈曲模态,需对解进行展开。
非线性屈曲分析是在大变形效应开关打开的情况下[NIGEOM,ON]的一种静力分析,该分析过程一直进行到结构的极限载荷或最大载荷。其它诸如塑性等非线性也可以包括在分析中。
在进行非线性的屈曲分析时,分析过程与一般的非线性分析过程相同。采用一系列子步以增量加载的方式施加一给定载荷直到求解发散。在很多情况下,为了有助于计算,应在模型上施加一初始缺陷(扰动)。预先进行一个特征值分析有助于非线性屈曲分析,特征值屈曲载荷是预期的线性屈曲载荷的上限,可以作为非线性屈曲分析的给定载荷,特征矢量屈曲形状可以作为施加初始缺陷或扰动载荷的根据。
以特征值的屈曲形状为基础定义初始几何缺陷的步骤如下:
1.建立没有初始几何缺陷的模型。
2.进行特征值屈曲分析。
3.用 UPGEOM 或 UPCOORD 命令来施加几何缺陷。
4.进行非线性屈曲分析。
建模时,采用pipe16单元来模拟支架结构中的各种杆件,用link180单元来模拟交叉支撑,用 combin14 单元来模拟其中的半刚性连接节点。
(1)pipe16 单元:pipe16 是一种单轴单元,具有拉压、扭转、和弯曲性能。该单元在两个结点上有 6 个自由度:沿节点 X,Y,Z 方向的平移和绕结点 X,Y,Z 轴的旋转(图3-1)。这个单元是建立在三维梁单元基础之上的,建模时可以直接输入钢管的内外径以及其他的实常数。支架中的杆件都是受压和受弯构件,因此可以用 pipe16 单元来模拟。
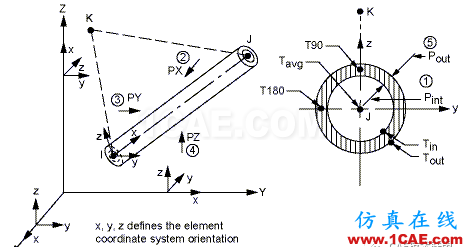
图3-1
(2)link180单元:link180单元是一种能应用于多种工程实际的杆单元,能被应用于桁架,垂缆,杆件,弹簧等。这个三维的杆单元只能承受单轴的拉压,每个节点上有三个自由度:X,Y和Z方向的位移(图3-2)。交叉支撑与门架立杆的连接为辊轴连接,只承受拉力或压力,因此,用 link180单元来模拟。


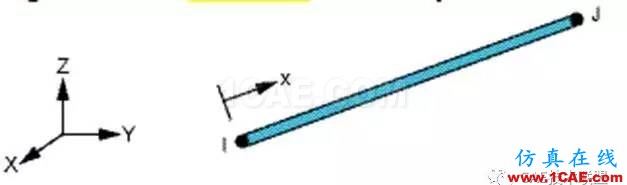
图3-2
(3)combin14 单元:combinl4 单元是一个具有非线性功能的单向单元,在一维、二维和三维的应用中,本单元都有轴向或扭转功能。轴向选项代表轴向拉压单元,每个节点具有 3 个自由度:沿节点坐标系X,Y,Z的平动,不考虑弯曲和扭转。扭转选项代表纯扭单元,每个节点也具有三个自由度:绕节点坐标轴X,Y,Z的转动,不考虑弯曲和轴向荷载(图3-3)
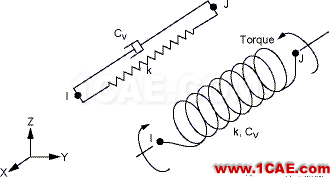
图3-3
一个力学问题需要满足三个条件:平衡条件、几何条件以及材料的本构关系。在平衡条件中,建立的方程可以将一个物体内部的应力与体力和作用在物体表面的外力联系起来,在非线性问题中,这些方程通常含有应力和位移。在几何条件中,建立的方程可以将物体内部的应变与物体的位移联系起来。显然,上述的平衡方程和运动方程与组成物体的特定材料无关,这些材料的影响由本构方程来表示,最常用的一种本构关系就是应力一应变关系。可以这样说,是应力和应变关系把平衡方程条件和几何方程条件联系起来,由这三种条件建立的方程表示了固体力学对自然规律的解答。本文所选用的钢材本构关系为理想弹塑性,本构关系如图3-4所示。
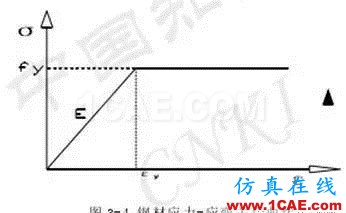
该曲线由钢材的弹性模量 E,单轴屈服应力 fy 来确定,钢材服从 Von-Mises屈 服 准则,钢材泊松比取 v=0.3 ,屈服强度为fy=235MPa ,弹性模量E=2.06e5MPa,屈服段的斜率取为 0。
支架结构中杆件的初始缺陷和扣件的连接质量差异都很大,对结构的受力性能有重要影响,不能忽略。因此在分析支架体系的极限承载力时,应对具有几何缺陷的钢管支架体系进行非线性分析。模拟几何缺陷一般有三种考虑方法,(1)是在结构上施加一个适时的瞬时面外作用,以激发屈曲响应;(2)是在建立模型时假设几何初始缺陷;(3)先进行特征值屈曲分析,找出结构最容易的变形形态,然后提取结构的微小变形来模拟初始缺陷,再进行非线性屈曲分析。本文钢管支架的有限元分析采用第三种方法来考虑结构的初始几何缺陷。
为分析竖向支撑对支架承载力的影响,参考规范中磨板支架结构体系的搭设方法,本文共建立三个不同竖向支撑形式的2列6跨4步(7.2m × 2.4m × 6m)的扣件式支架模型(图4-1,图4-2,图4-3)。
分析所建扣件式钢管支架有限元模型的计算结果,可知扣件式钢管支架的失稳形式是支架结构的整体失稳,其模态与竖向斜撑的设置方式有关。一般来说,扣件式钢管支架发生失稳破坏时,其对应的失稳模态根据竖向剪刀撑的设置不同,发生若干步距的半波失稳。
竖向剪刀撑是扣件式钢管支架结构体系的重要构件,具有不同竖向剪刀撑布置方式的支架每根立杆的稳定极限承载力见表4-4
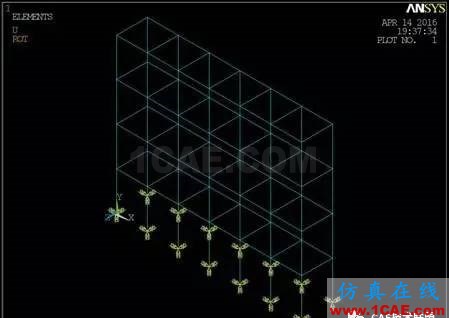
图4-1
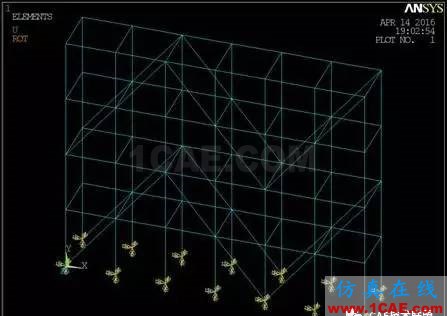
图4-2
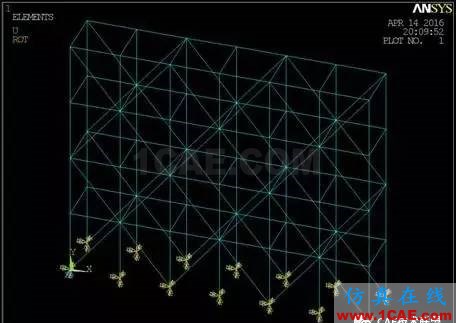
图4-3
|
编号 |
支撑情况 |
极限承载力 |
结果对比 |
|
1 |
不设竖向支撑 |
13.02 |
|
|
2 |
竖向单向支撑 |
14.39 |
10.5%
|
|
3 |
竖向交叉支撑 |
16.34 |
25.5% |
表4-4 不同竖向支撑形式对支架极限承载力的影响
竖向支撑是扣件式钢管支架体系的重要组成部分,决定了体系的侧向刚度和失稳模态,对整个支架的受力性能有很大影响,竖向支撑单向设置比不设支撑的极限承载力提高大约10%,而竖向交叉支撑又比单向支撑的极限承载力提高了15%,可见扣件式钢管支架中竖向支撑的设置方式对其的受力性能有明显的影响,为提高支架的安全性,不建议采用降低竖向剪刀撑侧向刚度的布置方式
本章利用 ANSYS 有限元软件对扣件式刚管支架结构体系进行了计算分析,主要工作有:总结了扣件式钢管支架的失稳模态及其影响因素;分析了水平剪刀撑,竖向剪刀撑对支架结构体系受力性能的影响。得到的结论有:扣件式钢管支架的失稳模态由竖向斜撑的设置方式决定,而失稳模态又决定了整个扣件式支架体系的极限承载力;扣件刚度对支架体系的极限承载力有一定影响;水平斜撑的设置对支架体系极限承载力的影响不显著;竖向斜撑的设置方式决定了支架体系的极限承载力;竖向斜撑单向设置对支架体系的承载力有一定影响。
通过改变竖向剪刀撑的设置形式,可以改变扣件式钢管支架体系的失稳模态,从而达到提高支架体系承载力的目的。因此,在实际搭设扣件式钢管支架体系时,应设法通过竖向斜撑的设置,提高体系的侧向刚度,打乱体系易发生的半波失稳模式,使各立杆失稳形式一致性较差,变形相互牵制。此外,由于竖向斜撑是扣件式钢管支架的主要侧向支撑,单向设置的竖向斜撑会对支架体系的受力性能有一定影响,因此不建议竖向斜撑单向设置,应按传统的交叉设置剪刀撑的方式搭设。
综合自网络
相关标签搜索:基于ANSYS的支架稳定性分析 Ansys有限元培训 Ansys workbench培训 ansys视频教程 ansys workbench教程 ansys APDL经典教程 ansys资料下载 ansys技术咨询 ansys基础知识 ansys代做 Fluent、CFX流体分析 HFSS电磁分析 Abaqus培训






