这是一个非线性的世界(Nonlinear World)
2017-03-23 by:CAE仿真在线 来源:互联网
线形(linear)和非线性(nonlinear)分析是有限元分析中两大“双塔”,线形问题总是我们所擅长或者乐意研究的,因为其够简单,分析成本低。但本质上说,这个世界主要还是非线性居多,线形总隐含着小变形、小应变、小的旋转、小的温度变化等等前提条件,但即使是“小”,也不会是数学上严格意义的真正线性,不会是一条完美的直线。不过你也不必惊慌,虽然不是完美的线形,但我们并不需要那么完美同样可以在“小”的前提下得到较为精确的结果,所以很多工程师都乐意把问题简化为线形分析。
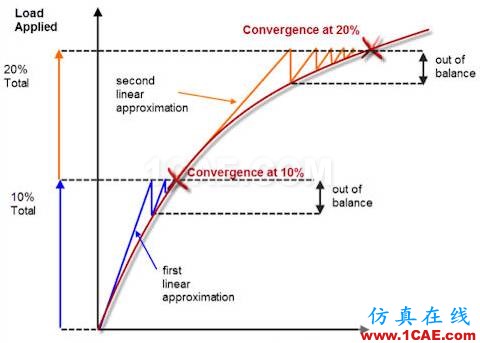
一旦我们进入非线性的世界,那么我们将踏上“未知”的旅程。下图展现了一个典型的非线性的历程。横坐标为位移,纵坐标为载荷,在非线性计算中,载荷的施加也是离散叠加的,如图中所示我们先施加10%的载荷(实际情况中没这么大,往往很小如0.1%),第一个线形逼近(有限元分析是数值算法,是多项式的线形逼近过程)没有收敛(没达到指定的收敛阈值),程序要继续寻找收敛点,经过几次逼近后才能找到收敛点,这才完成第一次的载荷收敛,下一步再增加10%的载荷,这个逼近过程也是类似的,直到完成100%的载荷加载。
这个过程是非常耗费成本的,因为每一步都需要对刚度矩阵(stiffness matrix)进行迭代,而一般线形分析只需要一个刚度矩阵即可,也就是说,如这个例子迭代十次的工作量(理想化的时间,成本)相当于线形分析的10倍,实际情况往往更多。
有些时候,我们不得不接受非线性,这一节我们主要讨论常见的几种非线性:
-
几何非线性(geometic nonlinaerity)
-
材料非线性(material nonlinearity)
-
接触非线性(contact nonlinearity)
1.几何非线性(geometic nonlinaerity)
几何非线性有时候又被叫做大变形分析(large displacement,但有些人并不同意这样叫,因为多大才算大变形呢并没有一个定量的约定),因为几何非线性往往涉及到大的位移,大的应变等等。
下面我们通过一个理论实例来说明几何非线性。如下图所示,一个杆件一端安装在铰链上,铰链上安装有扭簧(torsional spring)抵抗变形,杆件另一端施加有向上的一定大小的力F。我们来看看杆件旋转角度
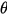
θ{\displaystyle \theta }
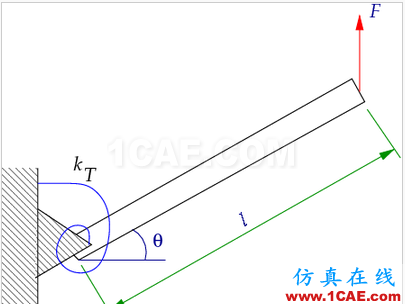
作用力对杆件端部产生的弯矩为:
-
M=Flcosθ{\displaystyle M=F~l~\cos \theta }
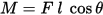
扭簧产生的扭矩为:
-
M=kTθ{\displaystyle M=k_{T}~\theta }
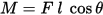
,
为扭簧系数
kT{\displaystyle k_{T}}联立上面两式有:
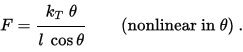
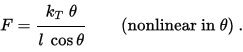
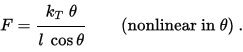
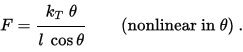
F=kTθlcosθ(nonlinear inθ).{\displaystyle {F={\cfrac {k_{T}~\theta }{l~\cos \theta }}\qquad ({\text{nonlinear in}}~\theta )~.}}
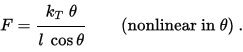
此时,很明显F和
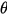
θ{\displaystyle \theta }
如果旋转角度θ{\displaystyle \theta }很小,比如
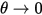
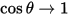
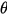
θ{\displaystyle \theta }
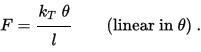
此时F和
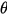
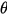
θ{\displaystyle \theta }
呈线形关系。
如果我们一开始就把问题简化为线形,那么如下图所示,线形结果和正确的非线性就有非常大的偏差,从图中可以看出,当旋转角度大于30°时,两种分析结果就分道扬镳了。
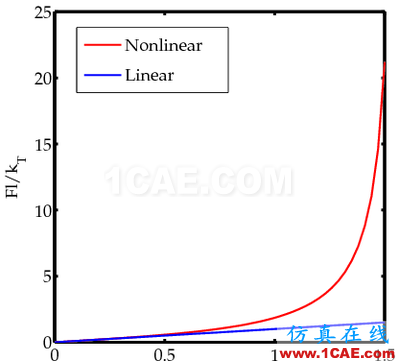
几何非线性在工程中非常常见。比如屈曲过程(buckling)就伴随着几何非线性,如下图所示。
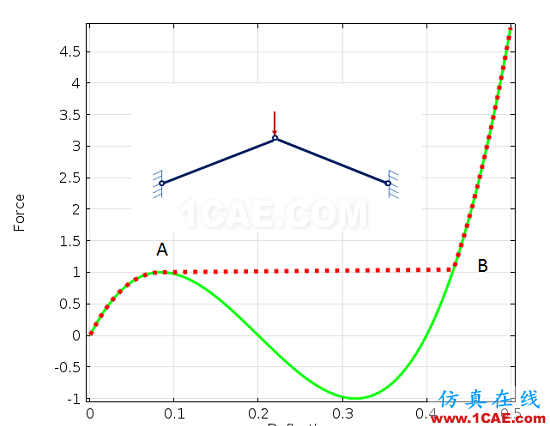
又比如一根梁两端约束的不同,受力情况也不同。如下图所示,一种情况是简支梁一端约束,另一端可以轴向活动;另一种情况是两段都受到约束。当施加垂直方向的载荷时,如果运用线形分析,那么结果没太大差比;当考虑非线性(几何非线性)时,结果将非常不同。

当考虑几何非线性时,简支梁的位移情况:
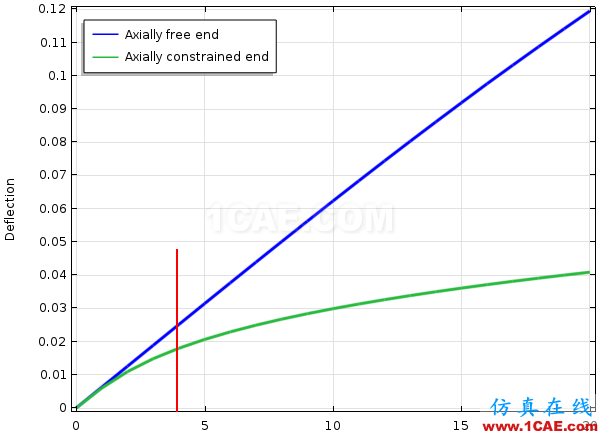
2.材料非线性(material nonlinearity)
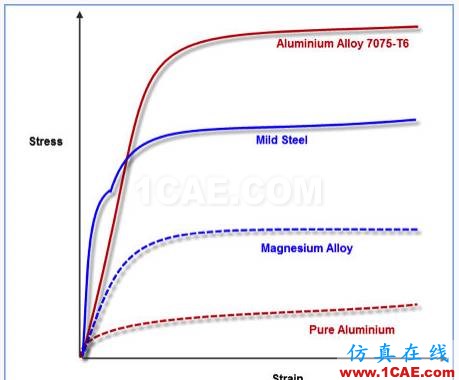
材料非线性应该是我们最熟悉的,在材料力学中主要讲的就是材料的非线性。当材料通过线形区域的屈服点(yield point)时,非线性的塑性(plastic)变形开始接管材料的变形形式,此时应力-应变将不再符合线形关系,
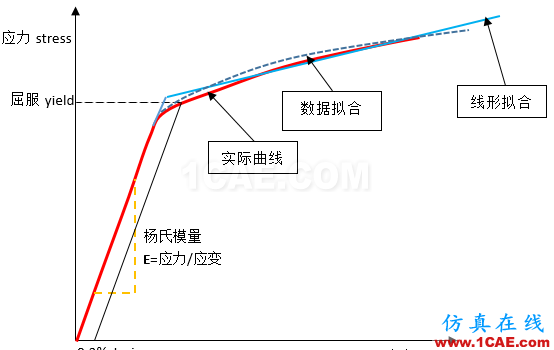
非线性分析中,步长大小的设定对非线性分析有很大的影响,过大的步长、高度非线性的事件或者接触条件的巨大改变,以及涉及到碰撞、断裂和高度屈曲的情况,求解器就需要长时间寻找到收敛的平衡点,有时候甚至找不到。但为了简化,对材料非线性来说,有些时候,在进入塑形变形后,我们同样可以进行线形简化。如下图所示,塑形阶段应力-应变的变化还是近似符合线形的,我们仍然可以通过线形拟合来进行替代,或者我们可以通过输入来自excel的数据来进行更精确的拟合。
同样我们可以用上面几何非线性的例子来说明材料非线性,在上面的计算中,我们是假定扭簧在旋转过程中材料属性是不会有变化的,但实际上随着纽簧的旋转会不断硬化,材料属性多少会有些变化(但很小)。为了说明材料非线性,我们假定扭簧系数Kt和角度成函数关系:
kt=k0+k1
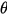
此时有扭簧的扭矩为:
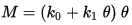
外部弯矩不变,此时可得:
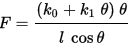
可以看出,此时公式既包含材料的非线性,也包含几何非线性。
同样的,如果旋转角度很小,此时有:
F=(k0+k1θ)θl(only material nonlinearity).{\displaystyle {F={\cfrac {(k_{0}+k_{1}~\theta )~\theta }{l}}\qquad ({\text{only material nonlinearity}})~.}
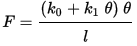
此时公式只包含材料非线性
下图综合绘制了几何+材料非线性、材料非线性、几何非线性和线性4种不同条件下力和角度的关系。
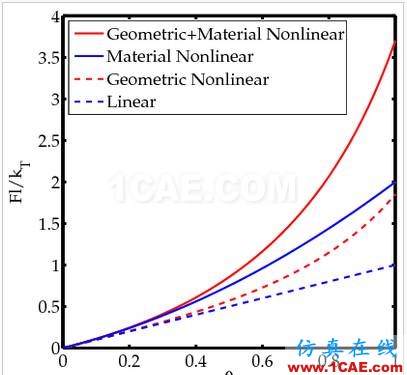
3.接触非线性(contact nonlinearity)
接触非线性顾名思义就是当两个对象发生接触时的现象,接触非线性和几何非线性类似,因为也是关于位移(变形)的函数,所以有些介绍中也把其归为几何非线性之中。
接触非线性的计算公式比较多,不同的接触类型适用于不同的公式,但在有限元分析时,一般都会引入“惩罚因子”(Penality Factor)这个物理量,以后我们会详细讲到。
下面列举了一些常见的非线性接触的例子:
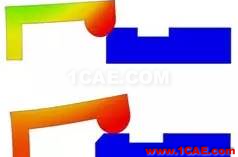
卡扣的安装过程
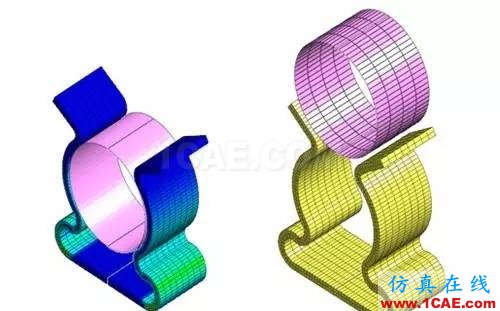
球状体装入夹持件的过程

轮胎和地面接触的过程

球状体和平面接触
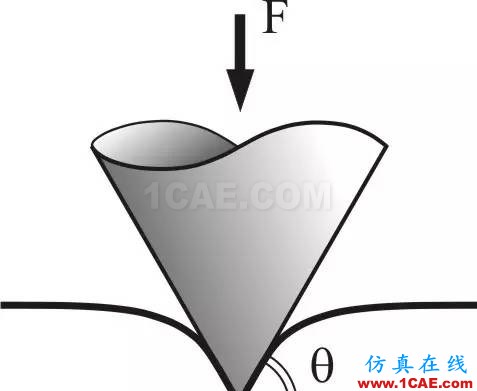
尖锐物与面接触的过程
非线性分析(nonlinear analysis)是有限元分析中非常重要的一个大类,我们以后会通过实例重点关注和讲解。
相关标签搜索:这是一个非线性的世界(Nonlinear World) Ansys有限元培训 Ansys workbench培训 ansys视频教程 ansys workbench教程 ansys APDL经典教程 ansys资料下载 ansys技术咨询 ansys基础知识 ansys代做 Fluent、CFX流体分析 HFSS电磁分析 Abaqus培训






