应力"奇点"（Stress singularity）（二）

2017-03-23  by:CAE仿真在线  来源:互联网

不久前,公众号发表了有限元分析中关于应力“奇点”(Stress singularity,或者叫应力的奇异性)的文章,引起了很大兴趣,至今文章都还在不断转发分享中。大家也纷纷留言表达自己的观点。请先阅读前面的文章,点此链接:应力"奇点"(Stress singularity)

今天,我们再对这个应力奇点(singularities)进行进一步的简单总结和讨论。

• 哪些情形会产生应力奇点?

• 怎样消除应力奇点?

• 什么情况下要注意应力奇点?
  

• 哪些情形会产生应力奇点

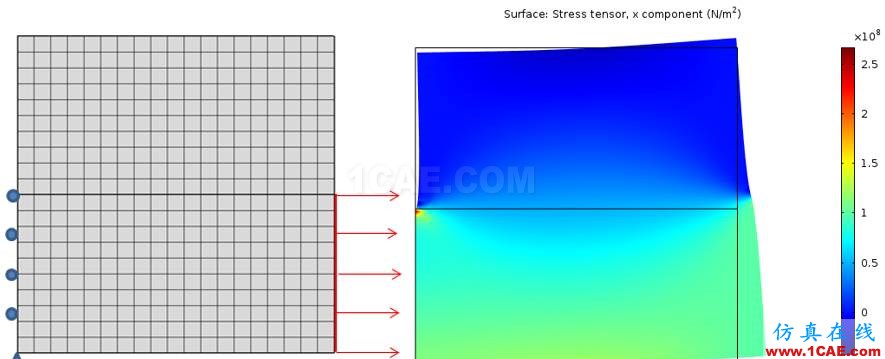
你可以用你的电脑尝试做下面这个简单的仿真测试,如下图所示,一个薄板部件(2m*1m)一段固定,另一端施加一个载荷,部件中央有一个正方形方孔(0.2m),不断将网格细化,看看正方形四个顶点的应力值大小。

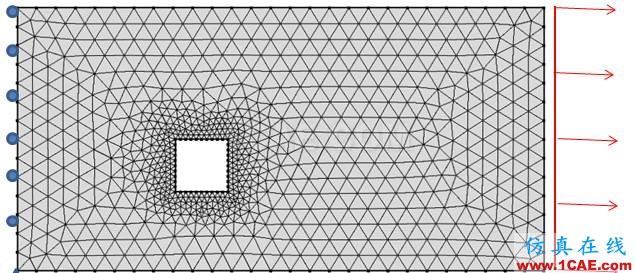随着网格的不断细化,你会发现四个顶点的应力值会越来越大,应力分布也越来越集中。

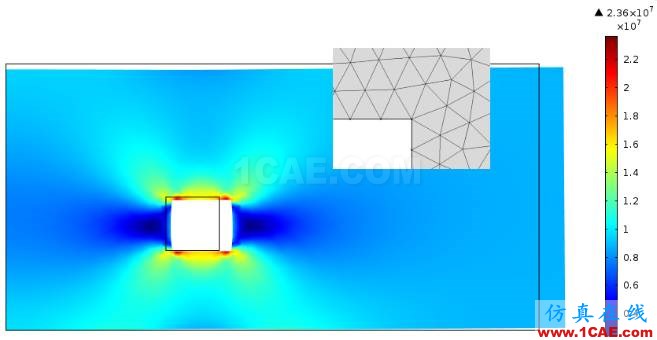
粗网格下的应力分布

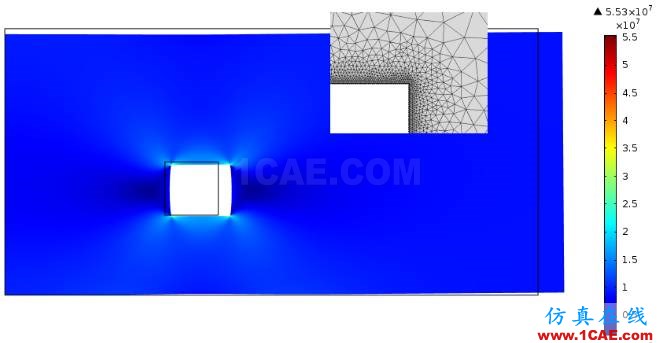
精细网格下的应力分布

如果你有耐心一直划分下去,会发现应力会不断增大趋于无穷,当然越往后网格划分会越来越困难。应力大小和单元大小的关系近似如下图(x坐标已经对数化处理)。

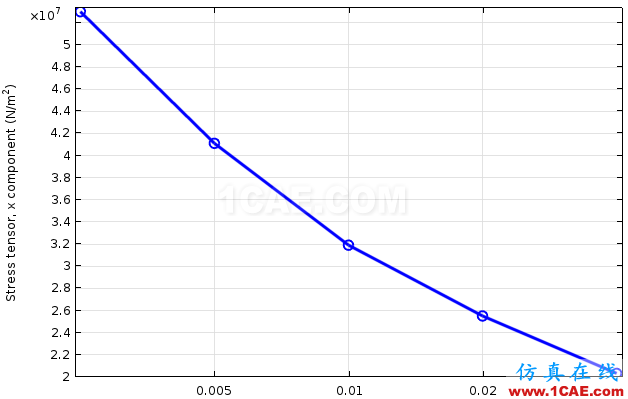
上面这个例子是一个非常容易理解的例子。这种随着网格划分不断细化,应力也不断增大的现象就是应力奇点,或者叫应力奇异性(singlarties)。

有些人可能会问,为什么应力会趋于无穷大,数学解释是什么。有限元的数学基础体系很繁杂,不是一个简单的公式可以说明的。不过有个不是很恰当但很直观的一个解释:

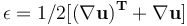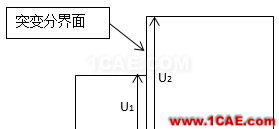
我们知道,有限元分析中,求得的结果是位移,然后应变由位移导出(,u为位移),应变是位移的梯度;然后应变再导出应力(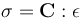),所以应力可以看做位移场的梯度或者位移的导数。如下图所示,在截面突变处,位移的大小也发生突变,在网格比较粗糙时这种突变不明显,但随着网格不断细化,突变会越来越明显,相应的导数也就越大,所以应力会不断变大。(但要说明的是,如果现实中有这么一个实实在在的部件,我们去验证,施加了载荷和约束,那么肯定只有一个确切无疑的状态,应力多大,位移多大是实实在在的可以测量出来的。在软件分析中,位移(displacement)是会收敛的,不会一直增大)。

应力奇点,往往主要是因为几何体局部没有圆角(截面积发生突变)产生应力集中导致的。还有就是前面提到的点加载;点约束也可能导致奇点;或者部件局部有狭小的缝隙;或者焊接件的焊缝处等等。

应力奇点的补充:

点约束

模型局部狭小的缝隙处

焊缝(焊接分析时)

• 怎样消除应力奇点?

消除应力奇点很简单,参照上面的例子,为了避免应力集中,我们倒圆角,避免缺口等等,至于点约束或者点加载,其实基本上我们一般压根不关注约束和加载处的应力分布。如果无法避免,根据圣维南原理(请参看前面的文章),远离奇点或应力集中的地方应力值不受影响。

• 什么情况下要注意应力奇点?

什么情况下我们要考虑应力奇点带来的影响呢?在现实生活中,上面提到的会产生应力奇点的理想情形是没有的,比如圆角,加工出来多少还是有的,只是有大有小,应力不会无穷大。但圆角越小应力越集中。

有些情况下应力集中我们是不用担心的,拿我们经常看到的窗户来说,如下图所示,拐角处并没有太大的圆角。为什么呢?因为建筑物主要承载的是静力。这种主要承载静力的情况下,应力集中是不会有显著危害的,我们可以不考虑。

再看一个窗户,如下图所示,飞机上的窗户,圆角就非常圆润。为什么呢,因为飞机在飞行过程中,外部压强不断变化,窗户的受力也会不断变化,这时候,这种受到载荷不断变化的情形,我们就要高度关注应力集中。

载荷不断变化带来的不良影响,就是有限元分析中的疲劳分析(fatigue analysis)。所以,当要对部件进行疲劳分析时,我们一点要关注应力奇点(或者应力集中),要处理好每一个细节处圆角的大小,因为应力的大小直接决定了我们疲劳分析出来的寿命,如果处理不好,实际情况和软件分析的结果将非常不同。

当然有个问题就是,如果我们要对一个非常大的模型进行疲劳分析,每个注意的细节都倒圆角,那圆角将会非常多,这会给网格划分带来很大的困难,不一定能划分成功,就算成功了,网格质量也可能很差,也非常多,那怎么办呢?这个问题将是我们后面要讨论的全局—局部分析(global to local),我们只把关心的区域处理好,即子模型(submodeling),然后截取出来分析。比如下图所示的轮毂,由于周期对称,我们只把轮毂的一小部分截取出来进行分析。局部分析的技巧我们会在后续文章中讨论。

相关标签搜索：应力"奇点"（Stress singularity）（二） Ansys有限元培训 Ansys workbench培训 ansys视频教程 ansys workbench教程 ansys APDL经典教程 ansys资料下载 ansys技术咨询 ansys基础知识 ansys代做 Fluent、CFX流体分析 HFSS电磁分析 Abaqus培训