应力"奇点"(Stress singularity)

2017-03-23 by:CAE仿真在线来源:互联网

在宇宙大爆炸理论中,“奇点”是宇宙演化的起点,它具有一系列奇异的性质,比如无限大的物质密度,无限大的压力,无限弯曲的时空等,同时在黑洞(blackhole)理论中,也将黑洞中心无限大的密度比作奇点。而在有限元分析FEA中,同样存在着“奇点”,那就是应力(stress)无穷大的点(随着网格细化无限增大的点)。

应力"奇点"(Stress singularity)ansys分析案例图片1

我们知道,有限元法是数值算法,而数值算法就涉及到解的收敛性,如果解没有收敛就可能导致奇点或者奇异性(singularity)的产生。今天我们将讨论应力“奇点”(stress singularity)。

应力奇点(Stress singularities)

在结构分析中,我们知道软件内部在计算时先计算出节点位移(displacements),然后再通过数学方程导出应力(stress)。应力奇点的出现往往就是某个节点的应力导出值不收敛,我们越是细化网格,此处的应力值就会越大,理论上,随着网格的细化,应力值会趋于无穷大(infinite)。

应力奇点发生的典型位置一般出现在点加载、点接触、点约束、90°拐角(无圆角)等位置。如下图所示的点加载和90°拐角的例子。

应力"奇点"(Stress singularity)ansys分析案例图片2

一个平板在端面的载荷,一个是集中在一点,一个是均匀分布在端面。在点加载附近会产生应力奇点,而均匀载荷不会。(但是比较两图可以发现,在稍微远离点载荷的地方,应力的分布和均匀载荷是一样的)

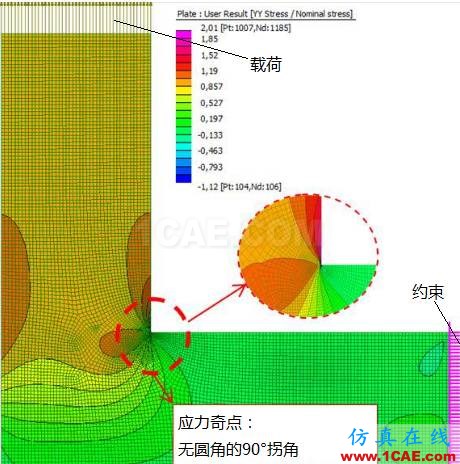
应力"奇点"(Stress singularity)ansys分析案例图片3

在90°拐角位置,最大压缩应力和最大拉伸应力发生在同一点,随着网格的细化,两种力都会随之不断增加。(当然,现实情况中,这种无圆角的部件是制造不出来的,多少会有个小圆角,所以不可能出现应力奇点,但根据圆角大小的不同,小圆角会产生应力集中)

圣维南原理(St. Venant’s Principle)

虽然应力在某些地方会趋于无限,而且是无法避免的。但这并不意味着模型在其它区域的结果不正确。

首先,位移在全局都是正确的,即使在应力奇点处位移也是正确的,不存在位移奇点一说。
其次,应力奇点只影响奇点附件比较小的区域,离开一定距离后,应力值仍然是对的。

这种情形就是有限元分析中有名的圣维南原理(St. Venant’s Principle)

圣维南原理(Saint Venant’s Principle)是弹性力学的基础性原理,是法国力学家圣维南于1855年提出的。其内容是:分布于弹性体上一小块面积(或体积)内的荷载所引起的物体中的应力,在离荷载作用区稍远的地方,基本上只同荷载的合力和合力矩有关;荷载的具体分布只影响荷载作用区附近的应力分布。还有一种等价的提法:如果作用在弹性体某一小块面积(或体积)上的荷载的合力和合力矩都等于零,则在远离荷载作用区的地方,应力就小得几乎等于零。不少学者研究过圣维南原理的正确性,结果发现,它在大部分实际问题中成立。

所以,有了圣维南原理,我们对有限元分析的模型处理就有了有力的理论支撑,比如对于我们不关心的区域我们完全可以简化模型方便计算和网格划分。

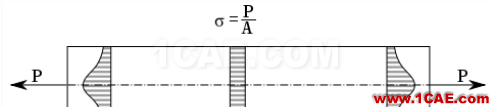
应力"奇点"(Stress singularity)ansys结果图片4

圣维南原理示意图,说明点加载影响的区域,在远离点加载区域,应力是分布均匀的

如何处理应力奇点

应力奇点在有限元分析FEA中很常见,但很多时候,奇点区域我们并不关心。所以

忽略应力奇点,如果不关心奇点区域的应力分布,根据圣维南原理,远离奇点的位置应力分布不受影响仍然是正确的。
另外,我们知道,在有限元分析划分网格时,过多的圆角,特别是小圆角会使网格划分出现问题,但有了圣维南原理,如果我们不关心圆角区域的应力分布,我们可以把小圆角去掉方便网格的划分,计算成本也会减小。
现实条件下,无限应力是不会产生的,比如90°拐角不可能加工出来。另外,由于材料本身会产生屈服,应力不可能无限增大。在非线性分析时,由于需要考虑材料的塑形区域,软件会自动消除应力奇点(因为过了弹性区域,塑形的存在使应力会有极限值)。

开放分享：优质有限元技术文章,助你自学成才