【技术篇】有相互依存关系的离散变量的ansys与workbench联合优化分析
2017-04-01 by:CAE仿真在线 来源:互联网
问题描述:
一平面结构钢组成的钢管桁架,受到载荷(单位N)和约束如下图所示。
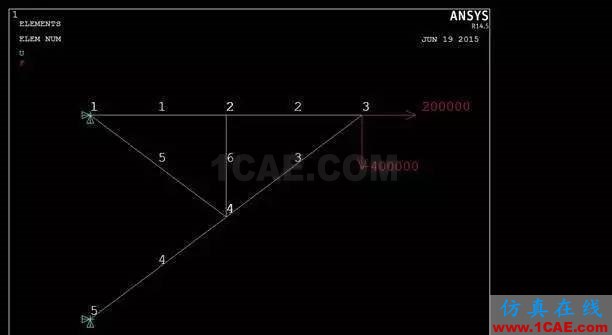
实际工程中,为了制造方便,通常选取单元1和单元2为一根杆(同一规格,杆总长为4m),单元3和4为一根杆(同一规格,杆总长5m)。节点2和4分别为中点。单元5和6为同一规格。
假设实际可供选择的钢管规格如下:共计14种

同时满足:
1.最大应力比RATIO不大于0.6(最大应力比等于最大应力与屈服应力比值)
2.压杆稳定系数MAXY不大于100
3.最大变形UY不大于10mm时的结构最小重量WT和各杆采用的圆管规格。
很明显这里需要采用杆单元建模。杆单元建模需要提供各个单元的实常数以获得各钢管的截面积。
问题分析:
1. 根据要求可知,该桁架结构最多采用3种规格,根据排量组合,最多拥有14*14*14=2744种组合。最原始的方法可以将其逐一计算,然后进行分析和比较。对于简单系统这种方法有一定的可行性,但是如果问题复杂程度增加,如鸟巢结构采用了多种不同规格的型材。如果可供选择的钢管规格增加,比如增加至 100种,甚至更多,即便是对于本问题这种方法也将有100*100*100=1000000,很显然该方法不可取。
2.如果采用ansys自身提供的优化方法,不管是采用以外径和壁厚为变量,还是直接以钢管的截面积作为变量。都不是特别方便。原因在于,这采用这两种优化思路,最终得到的优化结果均为连续变量。
3.workbench 提供了各种不同的强大的优化算法。单就优化变量的种类而言,可以支持连续变量和离散变量。但是无法将多种离散变量捆绑在一起。就本问题而言,系统可以分别将外径和壁厚作为离散变量,但是二者之间却没法关联在一起。也即使,可能最终得出某杆的外径为60mm,壁厚为5mm.查规格表可知,根本没有对应的钢管规格。当然对于本问题,可以先将各种不同规格的钢管的截面积求出来,然后直接在workbench中以截面积为离散变量。最终得到的离散结果(截面积), 反过来对照即可求出各钢管规格。但是这种方法有很大的局限性。如果问题的要求和复杂程度增大,该方法就很难可行了。比如,两种或多种不同规格的钢管的截面积是相等的,但是材料性能(如弹性模量)是不相等的(相当于关键变量是外径,壁厚和弹性模量)。简而言之,单独优化某一个杆件的某一个变量不能最终得到优化结果,原因在于需要优化的单一杆件的变量参数是相互依存,统一在一起的。
那么是否存在一种更为直接和有效方式呢?
这里提供一种优化思路,首先将非均匀离散变量均匀离散,即将规格表按照次序,进行依次编号。对于本问题,根据规格的种类,依次编号为为1~14.那么最终优化变量就是各杆的规格编号。采用ansys建立规格表格,利用workbench的离散优化功能,调用ansys分析问题(规格表存在ansys分析文件中)。
具体的分析历程如下:
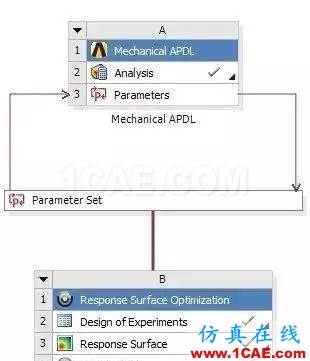
最终得到优化结果:

最终得到,横杆采用规格表中第12的材料,斜杆采用规格中第11种材料,中间连杆为规格表中第1种材料。
需要说明的是对应基于离散变量的优化,采用不同的响应面构建方法和优化算法,效率相差特别大。即使对于本问题节点数目5个,单元数目6个。选择的响应面构建方法和优化算法不同,也有可能计算几个小时。对于本问题采用Latinhypercube sampling(LHS拉丁超立方体抽样)生成试验设计,采用神经网络方法来构建响应面,实际证明效率较高。
另外对应基于离散变量的优化分析,目前workbench只支持筛选法和混合整数序列二次规划优化算法。
另外,其实该问题也可以完全采用ansys经典完成程序优化设计,利用离散编码陷阱实现从连续变量到离散变量的转变。但是该方法也有很多缺点:
1.最终得优化的变量依然是连续的,需要人为后处理,实现规格表的编码。
2.最终得到的优化结果,可能陷入局部最小陷阱。采用首次得到的优化结果为初始值,然后缩小优化变量的采用空间,可以一定程度上改善结果的精度。
3.规格表的离散区间步长对于求解的效率的影响非常大。因此,需要增大优化迭代次数。
4.系统优化过程中,可能多次在等效解处徘徊。影响求解效率。
5.人为将连续变量离散化后,基于偏导算法的一阶优化方法将不能处理该类问题。
6.最终解码得到的材料规格往往需要返回到分析中去,才可以得到真实的状态变量数值。
相关标签搜索:【技术篇】有相互依存关系的离散变量的ansys与workbench联合优化分析 Ansys有限元培训 Ansys workbench培训 ansys视频教程 ansys workbench教程 ansys APDL经典教程 ansys资料下载 ansys技术咨询 ansys基础知识 ansys代做 Fluent、CFX流体分析 HFSS电磁分析 Abaqus培训






