瞬态动力学专题-单自由度系统自由振动ANSYS分析
2017-04-26 by:CAE仿真在线 来源:互联网
瞬态动力学分析(亦称时间历程分析)是用于确定承受任意的随时间变化载荷结构的动力学响应的一种方法。可以用瞬态动力学分析确定结构在稳态载荷、瞬态载荷和简谐载荷的随意组合作用下的随时间变化的位移、应变、应力及力。载荷和时间的相关性使得惯性力和阻尼作用比较重要。如果惯性力和阻尼作用不重要,就可以用静力学分析代替瞬态分析。
瞬态动力分析用在以下的设计中:
-
承受各种冲击载荷的结构,如:汽车中的门和缓冲器、建筑框架以及悬挂系统等。
-
承受各种随时间变化载荷的结构,如:桥梁、地面移动装置以及其它机器部件。
-
承受撞击和颠簸的家庭和办公设备,如:便携式电话、笔记本电脑和真空吸尘器等。
下面将展现最简单的单自由度系统的自由振动的瞬态动力学ANSYS分析,重点在于掌握瞬态动力学的分析方法,特别是时间离散中时间步长的选取、初始条件的施加(本题为初位移)、时间历程后处理等。进行模态分析计算固有频率,其目的是为了时间步长的选取,时间步长一般取固有周期的1/40~1/20,采用此方法确定复杂模型的时间步长非常有用。
一、问题描述
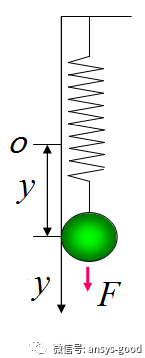
一个单自由度系统的自由振动,质量m= 0.5 kg,刚度k=5 kN/m,初始向下受拉力,使弹簧伸长0.2m,然后突然释放,计算位移随时间历程响应情况。
阻尼比取4种:
阻尼比1:ξ=0.0(无阻尼);
阻尼比2:ξ=0.02(欠阻尼);
阻尼比3:ξ=1.0(临界阻尼);
阻尼比4:ξ=2.0(过阻尼)。
问题分析:
单自由度系统采用COMBIN40建模,实常数中输入刚度k,阻尼系数c和质量m。采用Newmark直接积分法,时间步长取固有周期1/30,约为0.002s。

阻尼比1:ξ=0(无阻尼)时,阻尼系数c=0;
阻尼比2:ξ=0.02(欠阻尼)时,阻尼系数c=2;
阻尼比3:ξ=1.0(临界阻尼)时,阻尼系数c=100;
阻尼比4:ξ=2.0(过阻尼)时,阻尼系数c=200。
计算结果:ANSYS计算得出的固有频率为15.915Hz,不同阻尼比条件下得出的位移随时间变化曲线见下图。

二、GUI步骤
(一)建立模型
1.进入ANSYS
程序→ ANSYS 15.0→ ANSYS Product Launcher→ 改变working directory到指定文件夹→ 在job name输入:file。
2.设置计算类型
Main Menu> Preferences→选择Structural→ OK。
3.定义单元属性
(1)定义单元类型
Main Menu> Preprocessor>Element Type> Add/Edit/Delete→ Add→ 选择COMBIN40单元,即在左列表框中选择Combination,在右列表框中选择Combination 40→ OK。

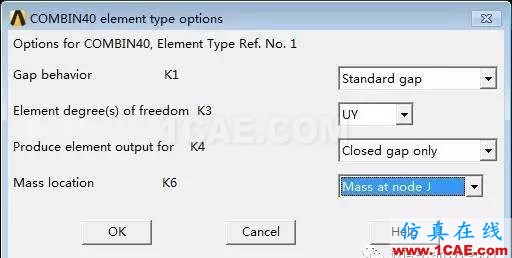
(2)单元选项设置:选中COMBIN40单元→ Option→ 在K3中选择UY;在K4中选择Closegap only;在K6中选择Mass at node J→ OK→ Close。
4.定义实常数
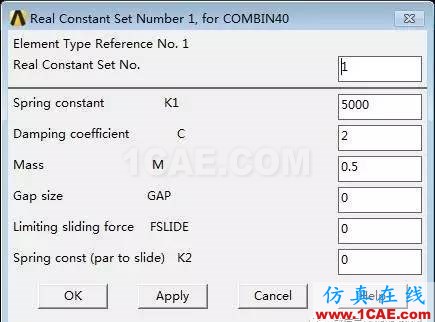
Main Menu> Preprocessor> Real Constants> Add→Type 1→ OK→ Real Constant Set No.:1,弹簧刚度K1:5000,阻尼系数C:2,质量M:0.5→ OK→ Close。
5.建立模型
(1)创建节点:Main Menu > Preprocessor> Create > Nodes> In Active CS→ NODE:1,X,Y,Z:0,0,0→ Apply→ NODE:2,XYZ输入0,-0.5,0。
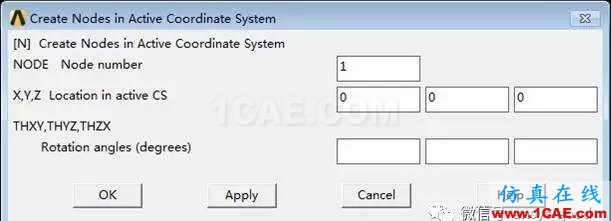
(2)创建单元:
①Main Menu> Preprocessor> Create> Elements>Auto Numbered> Thru Nodes→ 输入节点1,回车,再输入节点2→ OK。第1个节点是节点I,第二个节点是节点J。
②查看单元属性:Utility Menu> List> Elements>Nodes + Attributes。
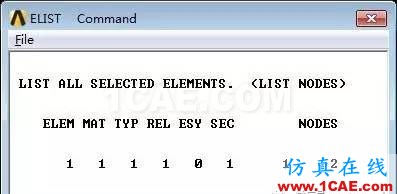
6.施加约束
Main Menu> Solution> Define loads> Apply> Structural>Displacement> On Nodes→ 拾取节点1→ OK→ Lab2:UY→ OK。
7.保存模型
Utility Menu > Files > Save as→ Save Database to输入mesh.db→ OK。
(二)模态分析,计算固有频率
1.模态分析求解
(1) 进入求解器:Main Menu> Solution。
(1)指定分析类型为模态分析:Main Menu > Solution >Analysis Type > New Analysis→ Modal→ OK。重要步骤!
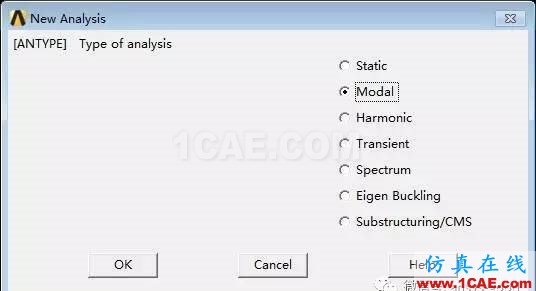
(2)设置模态分析选项:Main Menu > Solution >Analysis Type > Analysis Options→ Mode extraction method:Block Lanczos(模态提取方法,默认);No. of modes to extract(模态提取阶次):2;NMODE No. of modes to expand(模态扩展阶次):2→ OK。
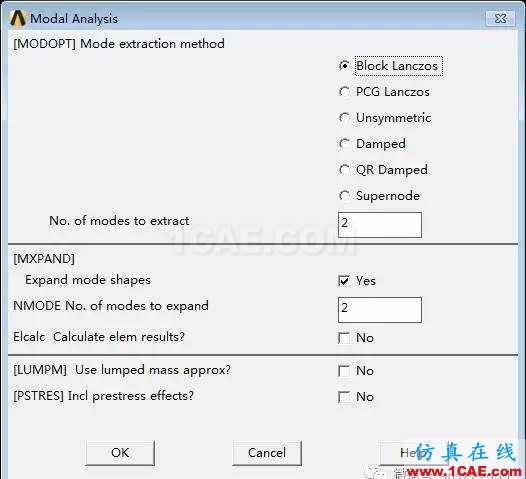
(3)求解:Main Menu > Solution >Solve > Current LS→ File > Close→ Solve Current Load Step→ OK→ Solutionis done→ Close。
2.后处理
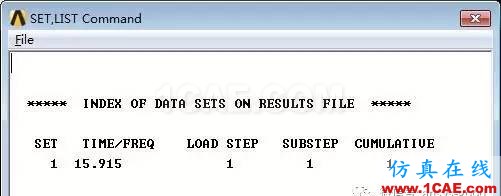
列表查看各阶固有频率:Main Menu > GenenralPostproc > Results Summary→ 记录各阶固有频率,对应的是TIME/FREQ。单自由度只有第1阶固有频率,固有频率为15.915Hz,固有周期1/15.915=0.0628s。
(三)瞬态动力学分析
1.调入模型
Utility Menu > Files > Resum from→ 选择mesh.db→ OK。
2.瞬态动力学分析设置
(1) 进入求解器:Main Menu> Solution。
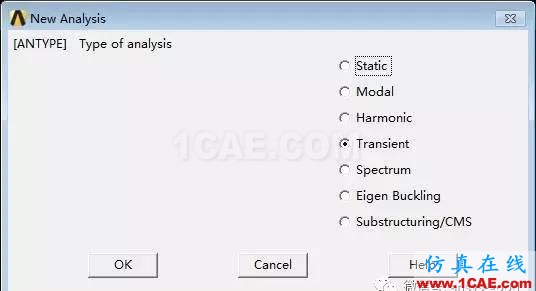
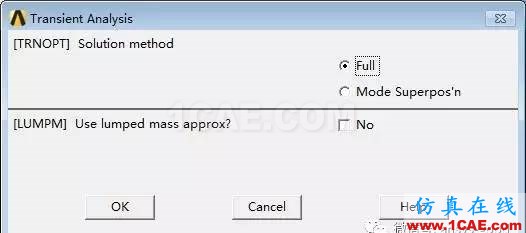
(2) 设置分析类型:Main Menu> Solution>Analysis Type> New Analysis→ 选择Transient→ OK→ 求解方法选择Full(完全积分法)→ OK。
3.第1载荷步求解设置
(1) 求解控制设置:Main Menu> Solution> AnalysisType> Sol’n Controls。
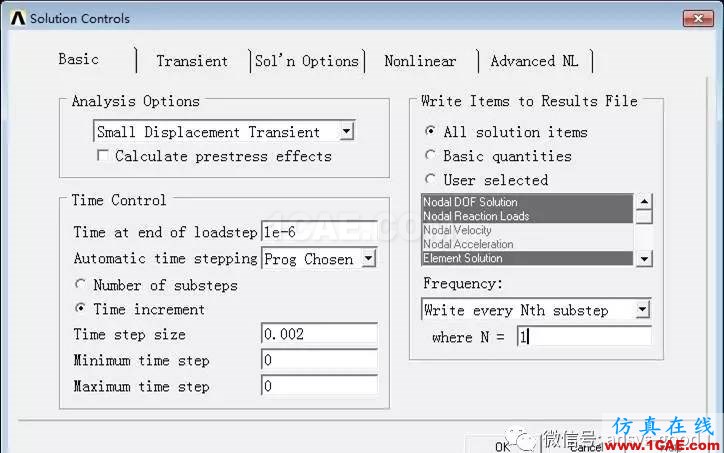
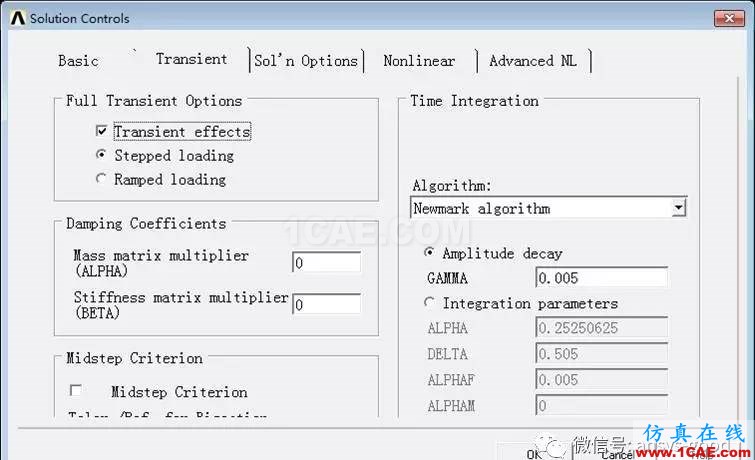
① Basic:时间控制Time Control中, Time at end of loadstep(载荷步结束时间):1e-6;Time increment(时间增量)中Time step size(时间步长):0.002;Frequency(输出频率)中选择Write every Nth substep,where N=1。时间步长取固有周期0.0628s/30约为0.002s。
② Transient:Full Transient Option中选择Transient effects(瞬态影响),选择Stepped Loading(阶跃加载)。
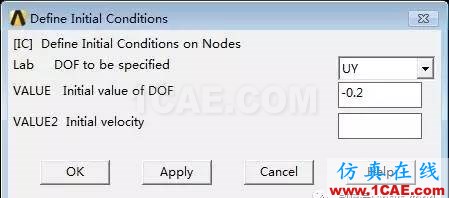
(2) 设置初值条件:Main Menu> Solution> DefineLoads> Apply> Initial Condit'n> Define→ 拾取节点2→ OK→ Lab:UY;VALUE:-0.2→ OK。
(3) 保存求解前文件:Utility Menu> Files>Save as→ 输入Load.db→ OK。
(4) 求解:Main Menu> Solution>Solve> Current LS→ File> Close→ Solve Current Load Step→ OK→ Solution isdone→ Close。
4.第2载荷步求解设置
(1) 求解控制设置
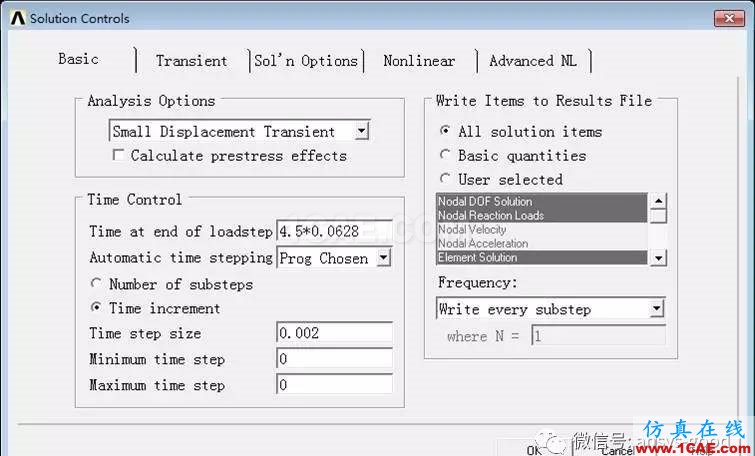
Main Menu> Solution> Analysis Type> Sol’nControls→ Basic:时间控制Time Control中,Time at end of loadstep:4.5*0.0628。
(2) 求解:Main Menu> Solution>Solve> Current LS→ File> Close→ Solve Current Load Step→ OK→ Solution isdone→ Close。
5.时间历程后处理
(1) 进入时间历程后处理器:Main Menu> TimeHistPostpro。
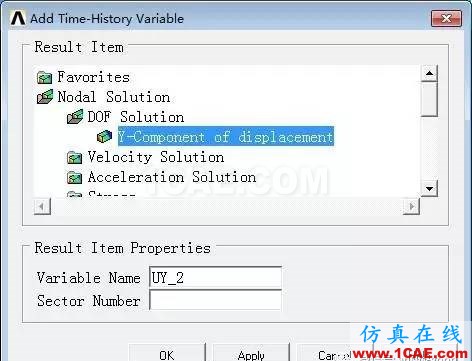
(2) 定义位移随时间变化变量:Main Menu> TimeHist Postpro> VariableViewer→ 选择红色方框中的按钮→ DOF Solution→ Y-Component of displacement→ OK→ 输入节点2→ OK。
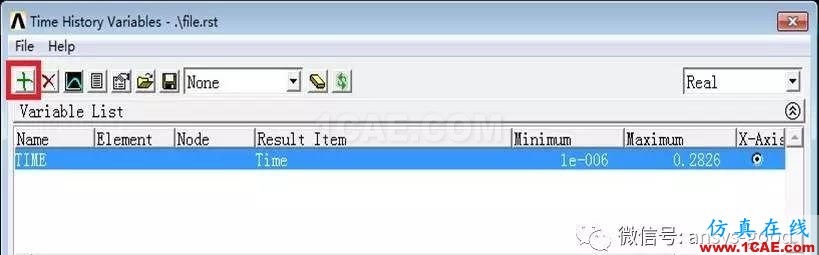
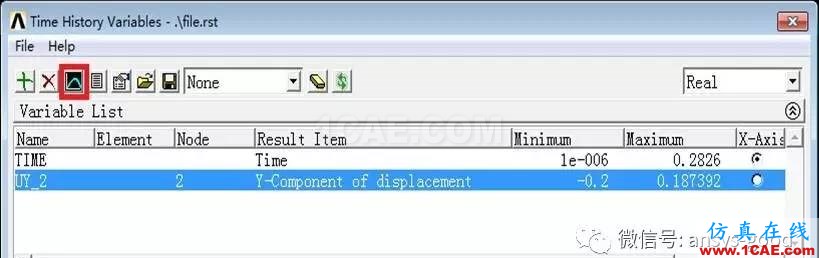
(3)显示位移随时间变化曲线:Main Menu> TimeHistPostpro> Variable Viewer→ 选中UY_2→ 选择红色方框中的按钮。
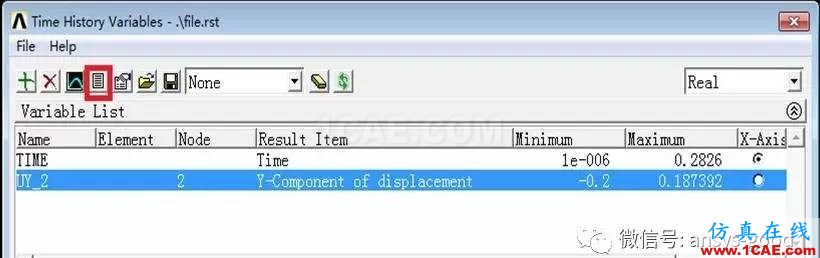
(4)列表显示位移随时间变化数据:Main Menu> TimeHistPostpro> Variable Viewer→ 选中UY_2→ 选择红色方框中的按钮。
三、ADPL步骤
k1=5e3 !刚度
m1=0.5 !质量
pi=acos(-1)
fre1=(1/(2*pi))*(k1/m1)**0.5 !固有频率,Hz
T1=1/fre1 !固有周期,s
Dt= T1/30
kesi=0.02 !阻尼比或相对阻尼系数0/0.02
c1=2* Kesi*( m1*k1)**0.5 !阻尼系数
/PREP7 !进入前处理器
ET,1,COMBIN40 !单元类型
KEYOPT,1,3,2 !单元的自由度UY
KEYOPT,1,4,1 !关闭间隙
KEYOPT,1,6,2 !质量在J节点
R,1,k1,c1,m1 !弹簧刚度、阻尼系数和质量
N,1,0,0,0 !创建节点1
N,2,0,-0.5,0 !创建节点2
E,1,2 !创建单元
D,1,UY !施加约束
FINISH !退出前处理器
SAVE,mesh,db, !保存模型
/SOLU !进入求解器
ANTYPE,2 !模态分析
MODOPT,LANB,2 !提取前2阶
MXPAND,2, , ,0 !扩展前2阶
SOLVE !求解
FINISH !退出求解器
/POST1 !通用后处理
SET,LIST !列固有频率结果
RESUME, mesh,db, !读入模型
/SOLU !进入求解器
ANTYPE,TRANS !瞬态动力学分析
TRNOPT,FULL !完全积分法
TIME,1E-6 !第1载荷步
DELTIM, T1/30 !积分时间步长
OUTRES,ALL,1 !输出每步结果
KBC,1 !阶跃加载
IC,2,UY,-0.2 !初始条件
SOLVE !求解
TIME,4.5*T1 !第2载荷步
SOLVE !求解
FINISH !退出求解器
/POST26 !进入时间历程处理器
FILE,,RST !调入结果文件
NSOL,2,2,U,Y,1UY !节点2的Y向位移
NPRINT,1 !每1个点打印1次
PRVAR,2 !画图显示曲线
/XRANGE,0,4.5* T1 !X轴范围
PLVAR,2 !画图显示曲线
相关标签搜索:瞬态动力学专题-单自由度系统自由振动ANSYS分析 Ansys有限元培训 Ansys workbench培训 ansys视频教程 ansys workbench教程 ansys APDL经典教程 ansys资料下载 ansys技术咨询 ansys基础知识 ansys代做 Fluent、CFX流体分析 HFSS电磁分析 Abaqus培训






