接触问题的非线性有限元分析
2017-07-12 by:CAE仿真在线 来源:互联网
引言
在工程结构中,经常会遇到大量的接触问题。火车车轮与钢轨之间,齿轮的啮合是典型的接触问题。在水利和土木工程中,建筑物基础与地基,混凝土坝分缝两侧,地下洞室衬砌与围岩之间,岩体结构面两侧都存在接触问题。对于具有接触面的结构,在承受荷载的过程中,接触面的状态通常是变化的,这将影响接触体的应力场。而应力场的改变反过来又影响接触状态,这是一个非线性的过程。由于接触问题对工程实践的重要性,本章将作为专门问题进行研究。
最早对接触问题进行系统研究的是H. Hertz,他在1882年发表了《弹性接触问题》一书中,提出经典的Hertz弹性接触理论。后来Boussinesg等其他学者又进一步发展了这个理论。但他们都是采用一些简单的数学公式来研究接触问题,因而只能解决形状简单(如半无限大体)、接触状态不复杂的接触问题。
二十世纪六十年代以后,随着计算机和计算技术的发展,使应用数值方法解决复杂接触问题成为可能。目前,分析接触问题的数值方法大致可分为三类:有限元法、边界元法和数学规划法。
数学规划法是一种优化方法,求解接触问题时,根据接触准则或变分不等式建立数学模型,然后采用二次规划或罚函数方法给出解答。
边界元方法也被用来求解接触问题,1980年和1981年,Anderson先后发表两篇文章,用于求解无摩擦弹性接触和有摩擦弹性接触问题。近年来虽有所发展,但仍主要用于解决弹性接触问题。
就目前的发展水平来看,数学规划法和边界元法只适合于解决比较简单的弹性接触问题。对于相对复杂的接触非线性问题,如大变形、弹塑性接触问题,还是有限元方法比较成熟、比较有效。
早在1970年,Wilson和Parsons提出一种位移有限元方法求解接触问题。Chan和Tuba,Ohte等进一步发展了这类方法。它的基本思想是假定接触状态,求出接触力,检验接触条件,若与假定的接触状态不符,则重新假定接触状态,直至迭代计算得到的接触状态与假定状态一致为止。具体做法是:
对于弹性接触的两个物体,通过有限元离散,建立支配方程
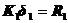 (5.1)
(5.1)
式中,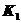 为初始的整体劲度矩阵,它与接触状态有关,通常根据经验和实际情况假定。
为初始的整体劲度矩阵,它与接触状态有关,通常根据经验和实际情况假定。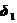 是结点位移列阵,
是结点位移列阵,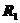 为结点荷载列阵。
为结点荷载列阵。
求解式(5.1),得到结点位移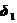 ,再计算接触点的接触力
,再计算接触点的接触力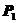 ,将
,将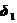 和
和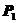 代入与假定接触状态相应的接触条件,如果不满足接触条件,就要修改接触状态。根据修改后新的接触状态,建立新的劲度矩阵
代入与假定接触状态相应的接触条件,如果不满足接触条件,就要修改接触状态。根据修改后新的接触状态,建立新的劲度矩阵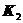 和支配方程
和支配方程
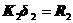 (5.2)
(5.2)
再由式(5.2)解得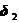 ,进一步计算接触力
,进一步计算接触力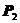 ,将
,将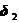 和
和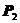 代入接触条件,验算接触条件是否满足。这样不断的迭代循环,直至
代入接触条件,验算接触条件是否满足。这样不断的迭代循环,直至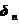 和
和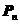 满足接触条件为止,此时得到的解答就是真实接触状态下的解答。
满足接触条件为止,此时得到的解答就是真实接触状态下的解答。
在以上的研究中,没有考虑接触面的摩擦力。不考虑摩擦力的接触过程是一种可逆的过程,即最终结果与加载途径无关。此时,只需要进行一次加载,就能得到最终稳定的解。如果考虑接触面的摩擦力,接触过程就是不可逆的,必须采用增量加载的方法进行接触分析。1973年,Tusta和Yamaji的文章详细讨论了接触过程的可逆性和不可逆性。
从Wilson和Parsons的方法可看出,每一次接触状态的改变,都要重新形成整体劲度矩阵,求解全部的支配方程,既占内存,又费机时。实际上,接触状态的改变是局部的,只有与接触区域有关的一小部分需要变动,为此又提出一些改进的方法。
1975年,Francavilla和Zienkiewicz 提出相对简单的柔度法。图1、示出两个相互接触的物体A和B,假定A上有外力R作用,B有固定边界。接触面作用在A上的接触力是
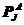 ,作用在B上的接触力是
,作用在B上的接触力是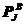 ,对于二维问题,
,对于二维问题,

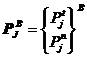 (5.3)
(5.3)
这些接触力是未知的,假定有m个接触点对,则增加了4m个未知量,为此需要补充4m个方程。现列出接触点的柔度方程
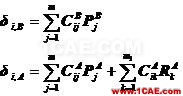 (5.4)
(5.4)
其中,
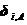 和
和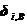 分别是物体A和B在接触点i处的位移,
分别是物体A和B在接触点i处的位移,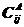 和
和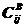 分别表示物体A和B因j点作用单位力时在i点引起的位移(即柔度系数)所组成的柔度子矩阵,m1是外荷载作用的点数,
分别表示物体A和B因j点作用单位力时在i点引起的位移(即柔度系数)所组成的柔度子矩阵,m1是外荷载作用的点数,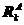 为第k个荷载作用点上的荷载向量。
为第k个荷载作用点上的荷载向量。
如果物体A和B之间的接触属于连续接触,则接触条件为
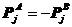 (5.5)
(5.5)
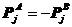 (5.6)
(5.6)
(5.5)和(5.6)是4m个补充方程,式中,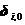 是第i个接触点对的初始间隙向量。由于式(5.6)的存在,令
是第i个接触点对的初始间隙向量。由于式(5.6)的存在,令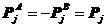 ,未知量数目减少,增加的未知量剩下2m个。将式(5.4)和(5.6)代入(5.5)得
,未知量数目减少,增加的未知量剩下2m个。将式(5.4)和(5.6)代入(5.5)得
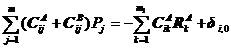 (5.7)
(5.7)
式(5.7)共有2m个补充方程。
对于滑动接触和不接触的自由边界,同样可根据相应的接触条件列出与式(5.7)类似的补充方程求解。
引入接触条件后,接触状态变化时,计算对象的整体劲度矩阵不再改变,出现的问题是增加了未知量数,需要建立补充方程。但由于补充方程(5.7)中,
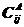 、
、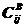 和
和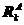 不随接触状态的改变而变化,而且接触点的数目远小于整体的结点数,因而可大大节约计算时间,提高了求解接触问题的效率。
不随接触状态的改变而变化,而且接触点的数目远小于整体的结点数,因而可大大节约计算时间,提高了求解接触问题的效率。
另外一种提高接触问题计算效率的方法是把接触点对作为“单元”考虑。1979年,Okamoto和Nakazawa提出“接触单元”,它是根据接触点对位移与力之间的接触条件建立的。接触单元和普通单元一样,可以直接组装到整体劲度矩阵中去。然后对支配方程进行“静力凝聚”,保留接触面各点的自由度,得到在接触点凝聚的支配方程。由于接触点数远小于结点数,凝聚后的方程阶数比未凝聚时方程阶数低得多。当接触状态改变时,只需对凝聚的支配方程进行修正和求解,因而可节约计算时间。
1975年,Schafer根据虚功原理推导了“连接单元”,也可以象普通单元一样地形成和组装到整体劲度矩阵中。连接单元包含有接触面的接触特性,通过改变形成单元的某些参数,来反映不同的接触状态。
1977年,J. T. Stadter和R. O. Weiss提出间隙元方法。“间隙元”是一种虚设的具有一定物理性质的特殊接触单元,其内部的应力应变反映了接触状态,并利用塑性力学中的“应力不变”准则来模拟接触过程。
目前的接触研究主要集中在弹性接触问题,关于弹塑性接触问题的研究也有了相当的进展,但有关大变形弹塑性接触的研究成果还很少。
弹性接触问题
基本假定
在分析弹性接触问题时,有如下的基本假定:
(1) 接触物体的材料是线弹性的,位移和变形是微小的;
(2) 作用在接触面上的摩擦力服从Mohr-Coulomb准则;
(3) 接触面连续平滑。
5.2.2 接触条件
所谓接触条件,是指接触面上接触点处的位移和力的条件。利用接触条件,可以判断接触物体之间的接触状态。接触状态可分为三类:连续接触,滑动接触和自由边界。为了更方便地表示接触条件,需要在接触面上建立局部坐标系
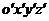 ,如图5.2所示。由于一般情况下,A、B两个物体在接触点处无公共切面和公共法线,因此,局部坐标系的
,如图5.2所示。由于一般情况下,A、B两个物体在接触点处无公共切面和公共法线,因此,局部坐标系的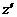 轴只能尽可能地接近公法线方向,
轴只能尽可能地接近公法线方向,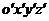 平面尽可能地接近公切面。
平面尽可能地接近公切面。
令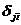 和
和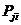 分别是第j个接触物体(j=A, B)沿第i个局部坐标(i=
分别是第j个接触物体(j=A, B)沿第i个局部坐标(i=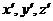 )的位移和接触力,则三类接触条件可表示为:
)的位移和接触力,则三类接触条件可表示为:
(1) 连续接触条件
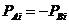 (i=
(i=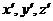 ) (5.8)
) (5.8)
 (i=
(i=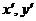 ) (5.9)
) (5.9)
同时要满足沿接触面的切平面方向不滑动的条件:
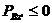 和
和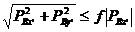 (5.10)
(5.10)
以上式中, 是接触面在
是接触面在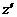 方向的初始间隙,f是接触面之间的滑动摩擦系数。
方向的初始间隙,f是接触面之间的滑动摩擦系数。
(2) 滑动接触条件
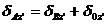 (5.11)
(5.11)
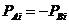 (i=
(i=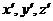 )或者表示为
)或者表示为
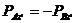 和
和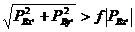 (5.12)
(5.12)
其中,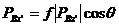 ,
,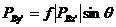 ,
,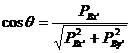
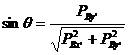
(3) 自由边界条件
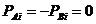 (i=
(i=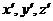 ) (5.13)
) (5.13)
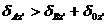 (5.14)
(5.14)
以上接触条件中出现的位移和接触力通常都是未知量,因此需要采用迭代算法,即首先假定接触状态,根据假定的接触状态建立有限元求解的支配方程,求解方程得到接触面的位移和接触力,并校核接触条件是否与原来假定的接触状态相符。若不同,就要修正接触状态,这样不断地循环,直到接触状态稳定为止。实际上,这是一个局部的几何非线性问题。
接触问题的可逆性
对于接触问题,存在可逆和不可逆两种接触状态。所谓“可逆”,是指沿不同的加载途径,其最终的结果是相同的。“不可逆”则是指对于不同的加载途径,最后的结果不同。发生不可逆过程的原因是由于接触面出现了滑动摩擦,下面的例子可以说明这一点。
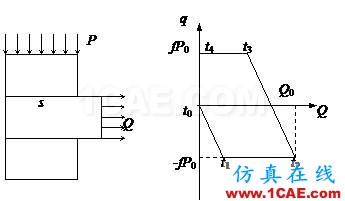
图5.3示出一个由A、B、C三个物体组成的接触问题。物体A上面作用有匀布荷载R,左边为铰支座。物体C左边和下面均有铰支座。物体B在匀布荷载Q的作用下,可以沿着上下两个接触面滑移。加载分三步:
(1) 施加荷载R,并保持R0不变;
(2) 施加荷载Q,从0增加到Q0;
(3) 逐渐减小荷载R,回到0。
现考察A、B接触面上某一点s的切向力q随荷载Q的变化过程。当Q=0时,假定q=0。随着Q的增大,q也增大,直到物体B发生滑动,此时q=-fP0,见图5.3中的t1点。q保持此值,直至Q=Q0为止,此时,相应的点为t2。接着,Q开始减小,从平衡的角度,q也减小,逐渐到零。由于这时Q还未减小到零,q会继续减小,实际上是改变符号,向相反方向增加,直到q=fP0(t3点),当Q减小到零时,回到点t4。
可以看出,由于接触面滑动摩擦的存在,最终状态t4与初始状态t0是不同的,说明切向接触力是不可逆的。
因此,凡是考虑接触面切向摩擦力的接触问题,都应当按复杂加载过程来研究,即通过增量的方式求解。对于不考虑摩擦的可逆过程,是一种简单加载过程,可以一步加载完成求解。
弹性接触问题有限元基本方程和柔度法求解
假设A、B是相互接触的两个物体,为了研究的方便,将它们分开,代之以接触力PA和PB,如图5.4所示。然后建立各自的有限元支配方程:
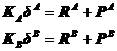 (5.15)
(5.15)
式中,KA、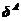 和RA分别是物体A的整体劲度矩阵、结点位移列阵和外荷载,KB、
和RA分别是物体A的整体劲度矩阵、结点位移列阵和外荷载,KB、
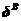 和RB分别是物体B的整体劲度矩阵、结点位移列阵和外荷载。
和RB分别是物体B的整体劲度矩阵、结点位移列阵和外荷载。
显然,接触力PA和PB都是增加的未知量,无法由式(5.15)求出,必须根据接触面上接触点对的相容条件确定。
设A、B上的接触点对为iA和iB(i=1, 2, …, m),假定劲度矩阵KA和KB非奇异,可求逆,则由式(5.15)得到接触点的柔度方程
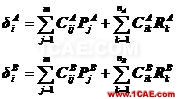 (5.16)
(5.16)
式中,i、j=1, 2, …, m表示结点号,m是接触点对数目,nA、nB分别为作用在物体A和B上外荷载的作用点数,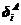 和
和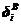 表示物体A和B上接触点i的位移
表示物体A和B上接触点i的位移
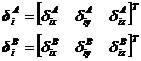
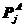 、
、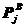 是A和B上接触点j的接触力
是A和B上接触点j的接触力
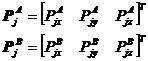
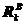 、
、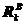 为A和B上结点k的外荷载
为A和B上结点k的外荷载
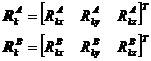
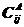 、
、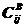 表示物体A和B上,由j点的单位力引起的i点在x、y、z三个方向的位移,是一个3×3阶的柔度矩阵。
表示物体A和B上,由j点的单位力引起的i点在x、y、z三个方向的位移,是一个3×3阶的柔度矩阵。
在列出相容条件,求解接触问题之前,有两个问题需要解决。
首先是消除刚体位移的问题。因为得到方程(5.16)的前提是KA和KB非奇异可求逆,也就是说物体A和B要有足够的约束,不会发生刚体位移。但是有些接触物问题中,可能会有某个物体由于约束不够产生刚体位移,此时须对刚体位移进行处理。
以图5.4中的物体A为例,假定它的约束不够,则KA为奇异矩阵,记为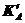 。引入虚拟的约束,消除A的刚体位移,则(5.15)的第一式可改写为
。引入虚拟的约束,消除A的刚体位移,则(5.15)的第一式可改写为
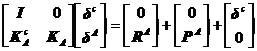 (5.17)
(5.17)
其中,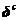 是与虚拟约束相应的位移向量,I是单位矩阵。由上式得到
是与虚拟约束相应的位移向量,I是单位矩阵。由上式得到
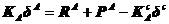 (5.18)
(5.18)
从式(5.18)导出物体A上接触点的柔度方程
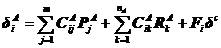 (i=1, 2, …, m) (5.19)
(i=1, 2, …, m) (5.19)
Fi是与刚体位移相应的柔度矩阵。
第二个问题是,要将上述整体坐标系下的量转化到接触面的局部坐标系
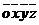 。接触点位移和接触力在不同坐标系下的表达式有以下的关系
。接触点位移和接触力在不同坐标系下的表达式有以下的关系
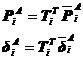 (A、B) (5.20)
(A、B) (5.20)
式中,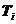 是结点i的坐标转换矩阵,
是结点i的坐标转换矩阵,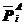 、
、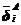 分别是接触面局部坐标系下,结点i的接触力和位移。将式(5.20)代入式(5.19),得
分别是接触面局部坐标系下,结点i的接触力和位移。将式(5.20)代入式(5.19),得
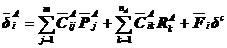 (5.21)
(5.21)
其中,
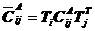 ,
,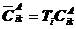 ,
,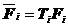 。同样,将式(5.20)代入式(5.16)的第二式,得
。同样,将式(5.20)代入式(5.16)的第二式,得
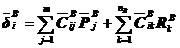 (5.22)
(5.22)
以下将针对三类接触条件建立相应的相容方程。
(1) 连续边界
根据前面的连续边界条件(5.9),可以建立接触点的位移相容方程
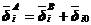 (5.23)
(5.23)
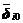 是第i个接触点对在局部坐标系下的初始间隙。将(5.21)和(5.22)代入(5.23),并注意有
是第i个接触点对在局部坐标系下的初始间隙。将(5.21)和(5.22)代入(5.23),并注意有
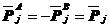 ,可得
,可得
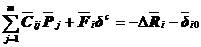 (5.24)
(5.24)
式中,
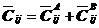 (5.25)
(5.25)
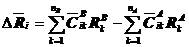 (5.26)
(5.26)
(2) 滑动边界
接触面局部坐标系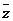 方向的位移仍然满足式(5.23),但在切平面的
方向的位移仍然满足式(5.23),但在切平面的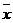 和
和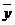 方向,接触力的合力已经达到摩擦极限,按照Mohr-Coulomb定律,则有
方向,接触力的合力已经达到摩擦极限,按照Mohr-Coulomb定律,则有
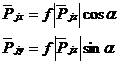 (5.27)
(5.27)
(3) 自由边界
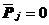 (5.28)
(5.28)
以上建立的相容方程,为原来的有限元支配方程增加了3m个补充方程,以求解3m个增加的未知接触力Pj (j=1, 2, …, m)。
在建立相容方程时,必须知道接触状态,而接触状态事先也是未知的,因此这是一个迭代求解的过程。一般先假定为连续接触状态,按式(5.24)建立全部接触点的相容方程,求出接触力后,验证接触条件是否满足连续接触,若是则不作修改;若为滑动状态,就用式(5.27)来代替这个接触点在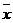 和
和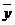 两个方向相应的方程;若是自由状态,就用式(5.28)替换这个接触点的所有相应方程。这样通过反复迭代,就可以求得真正的接触力和相应的相容方程。
两个方向相应的方程;若是自由状态,就用式(5.28)替换这个接触点的所有相应方程。这样通过反复迭代,就可以求得真正的接触力和相应的相容方程。
相容方程的增量形式
对于具有滑动摩擦的接触问题,由于接触过程的不可逆,需要采用增量方式加载、假定分级加载的次数为np,在进行第l级加载前已经施加的混杂为
 和
和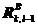 ,本级荷载增量为
,本级荷载增量为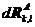 和
和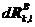 ,这样式(5.24)就变成
,这样式(5.24)就变成
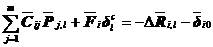 (5.29)
(5.29)
注意式中的各项有,
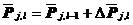
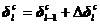
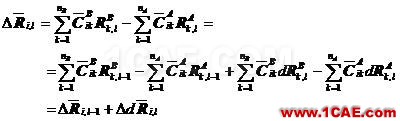
将上述各式代回式(5.29),得
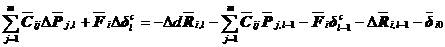 (5.30)
(5.30)
令
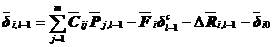 (5.31)
(5.31)
则(5.30)成为
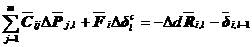 (5.32)
(5.32)
式(5.32)为连续接触条件相容方程的增量形式。
对于滑动接触条件,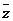 方向的相容方程与式(5.32)类似,
方向的相容方程与式(5.32)类似,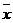 和
和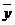 方向上相容方程的增量形式可表示为
方向上相容方程的增量形式可表示为
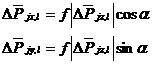 (5.33)
(5.33)
对于自由接触条件,相容方程的增量形式则为
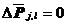 (5.34)
(5.34)
以上得到的接触点相容方程,由于刚体位移的存在,其未知量数目仍然大于方程数,因此必须补充整体平衡方程。
对于第l级加载,整体平衡方程为
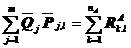 (5.35)
(5.35)
其中,
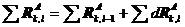
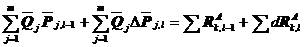
代入式(5.35)得
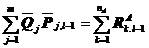 注意
注意
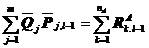
整体平衡方程为
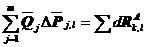 (5.36)
(5.36)
间隙元方法
上一节的柔度法对大面积的接触问题不合适,因为接触面积大,就需要布置比较多的接触点对,从而引起柔度矩阵求逆的困难。另外,对于多个物体的接触问题,柔度法还不够成熟。因此,对于大面积接触和多体接触问题,常常采用间隙元方法。
间隙元的基本思想是提高虚设的间隙单元来联接相互接触的物体,并人为构造单元的物理特性以模拟接触过程。
相关标签搜索:接触问题的非线性有限元分析 Ansys有限元培训 Ansys workbench培训 ansys视频教程 ansys workbench教程 ansys APDL经典教程 ansys资料下载 ansys技术咨询 ansys基础知识 ansys代做 Fluent、CFX流体分析 HFSS电磁分析 Abaqus培训






