CAE入门-材料力学的困惑
2017-09-28 by:CAE仿真在线 来源:互联网
计算机辅助工程(Computer Aided Engineering,CAE)是以专业计算机软件为工具,对工程中复杂产品的物理特性(如结构强度,刚度,稳定性,动力响应,三维多体接触,弹塑性,热传导,电磁场,流场的速度和压力等)进行分析计算及优化设计的一种近似数值分析方法。近些年以来,该技术在机械,汽车,航空,航天,电子产品,土木等领域得到了广泛的应用。
要了解该技术,我们可以从材料力学的局限性谈起。前面说过,材料力学主要以单根杆件为基础,研究其强度,刚度,稳定性问题。对于理想杆件发生的四种基本变形和组合变形,可以使用材料力学的研究成果来对其进行设计和校核。但实际工程结构是千变万化的,对于一个实际杆件结构,用材料力学的计算方法来计算,会遇到很多挑战,下面举例说明。
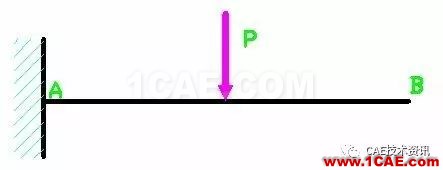
如下图所示的悬臂梁,在中间施加一个竖直向下的集中力P,要考察该梁的强度问题。使用材料力学的方法解决该问题是容易的。可以首先绘制出内力图,然后得到危险截面,接着在危险截面上找到危险点,根据该危险点的应力不要超过允许应力,就可以进行强度设计。
然而实际的结构总是比上图要复杂一些。在实际结构中,为了加强刚性,通常会增加支撑,如下图。直观的看,此时结构的刚性显然会提高,但是它给求解带来了麻烦。因为此梁左边是固定端,有3个约束力的未知数,右边有1个约束力的未知数,这样一共是4个约束力的未知数,但是根据理论力学,该梁只能列出3个独立的平衡方程,所以是不能求出所有的未知反力的。
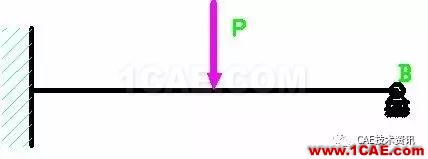
不能求出所有的未知反力,这导致无法求内力。因为内力是用截面法,对某一段列平衡方程得到的。外力不知道,内力就没有办法得到。不能得到内力,则不知道危险截面,从而不知道危险应力是多少,进行强度计算就成为空中楼阁。
上述问题在材料力学里面称为超静定问题。为了解决上述困境,材料力学使用了所谓的力法。力法的基本思路如下。
首先,把右边的滚动支座用一个向上的集中力F来取代如下图。因为滚动支座本来就是提供一个支持力的作用,所以这种取代并无问题。
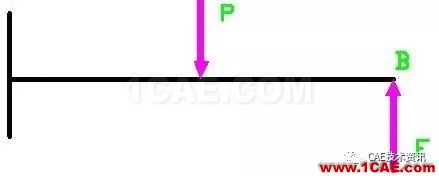
一旦取代以后,按照叠加法,该图可以分解为下面两种情况的叠加。
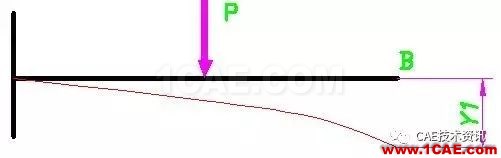

在第一种情况下,只有集中力P作用,在第二种情况下,只有集中力F作用。显然,我们可以使用材料力学求变形的方式,由P求出Y1,由F求出Y2.这就是说,Y1是P的函数,而Y2是F的函数。这里要注意,Y1与Y2是相等的。之所以相等,是因为B点本来就是一个滚动支座,它是不会有竖直方向的位移的。这样,根据Y1=Y2,就可以得到F与P的一个关系式。因为P是已知量,所以就可以求出F的大小。
这样,在得到F的大小后,再对原问题列出3个静力学平衡方程,共4个方程,就可以解出4个未知反力,此时,所有的外力都已知,从而可以求内力,求应力,进行强度计算了。上述方法称为力法。
力法看似很容易的解决了超静定问题,其实不然。考察下图所示的问题,此时B端是固定端,这样左边3个未知反力,右边3个未知反力,共有6个未知反力,所以需要补充3个方程,用上述方法仍旧可以得到这3个方程。但是实际问题的复杂性要远远超过该问题。
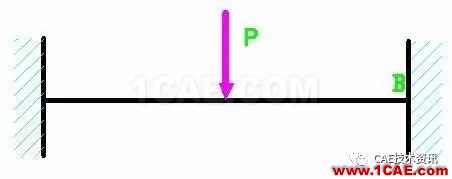
考察下叙钢架,整个结构都是焊接而成,在A端B端简支,而在钢架上某些节点处施加了向下的集中力,现在要求该梁的强度是否足够,也要计算最下面水平梁中间点的位移。
由于该钢架是一个构件,所以只能列出3个独立的平衡方程。但是其内部情况却很复杂,很难知道哪里最危险,即便知道了,也很难计算出其内力是多少。对于材料力学而已,这简直成为一个不可解的问题。
再如下图一个传动箱的支架,该支架是由一些方钢焊接而成,要对该支架进行强度计算,材料力学也是无能为力的。
以上两个问题的共性就在于,他们是超静定问题,而且超静定次数很高,就是说,要补充一大堆方程来求解外力。这使得上述所谓的力法在实践中很难使用。
对于上述问题,几乎只有CAE这种解决渠道。
从超静定的角度说明了材料力学的局限性,这里进一步说明材料力学对于其最擅长的单根杆件进行强度分析时的局限性。
考察如图所示的一根拉杆,在其上钻有一个孔。杆件两端受到的拉力P=80KN,杆长1米,截面为矩形,宽80mm,厚10mm,孔的直径为16mm,杆的许用拉应力为160MPa。试校核该拉杆的强度。

使用材料力学的观点来分析上述问题。这是一个拉伸变形问题,每个截面上内力都是P=80KN, 而通过孔中心的横截面面积最小,从而该截面上应力最大,其正应力是
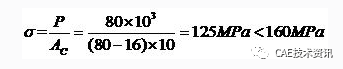
因此强度是足够的。
实际上,在C截面上存在应力集中,此截面上的应力并非均匀分布。使用有限元法(一种数值计算方法,该法是CAE的核心)计算的结果如下:
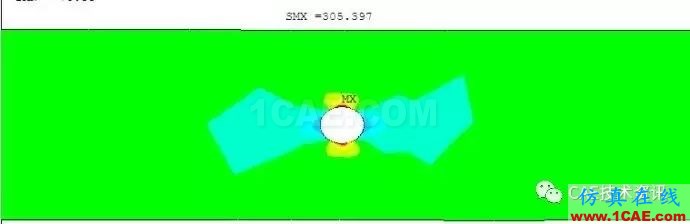
可以看到,中间截面的确最危险,其真实应力是305MPa,它是材料力学计算应力的2.44倍。此时强度是不合格的。
显然,在这种情况下,材料力学的计算结果完全不能够使用。材料力学之所以会出现这种问题,在于它在计算横截面应力的时候,假设该界面的应力是均匀分布的,而实际上并非如此,该截面在靠近孔的地方应力最大,在远离孔的地方应力越来越小。
轴是机械里面最常用的零件,为了连接其他零件,轴上面一般都有键槽,孔,台阶等结构。这些地方都存在着应力集中,直接使用材料力学的公式都会带来问题。
再如下面这根轴,中间是两个深沟球轴承进行支撑,而在最左边通过一个键槽连接一根连杆,在左右两边都与一块异型槽钢架连接,从而在轴上铣出两个平面并钻孔,其受力可以用如图所示的分布力系来表达,现在要对该轴进行强度校核。
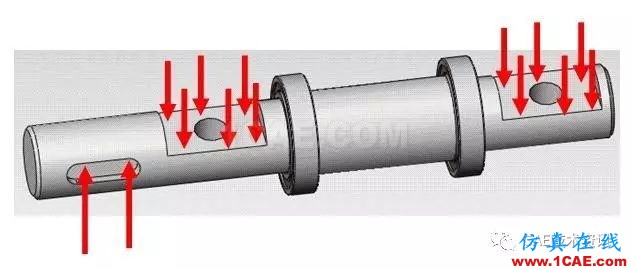
直观地看,由于有两个深沟球轴承支撑,该轴属于外伸梁形式。由于键槽受力并非在对称面上,所以这是一个弯扭组合问题。在铣削的平面处,存在应力集中,使用材料力学对该梁分析会遇到很大的困难。
经过精确分析所得到的该轴的应力云图如下:
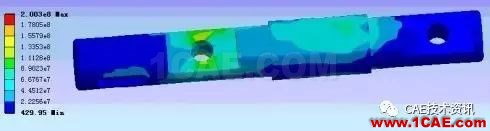
该云图用颜色显示了在轴上的应力分布情况。越近红色应力越大,越近蓝色应力越小。最大的应力出现在左边孔的下面如下图
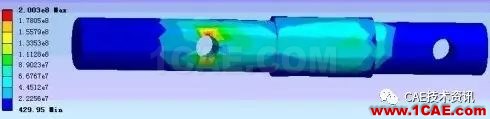
这种结果,如果不借助CAE,很难判断出最大应力在哪里。由于孔洞的出现,一些应力集中处成为危险截面,而这些地方的最大应力往往要超出材料力学计算的几倍,这使得材料力学在面对这些问题时显得有心无力。
相关标签搜索:CAE入门-材料力学的困惑 Ansys有限元培训 Ansys workbench培训 ansys视频教程 ansys workbench教程 ansys APDL经典教程 ansys资料下载 ansys技术咨询 ansys基础知识 ansys代做 Fluent、CFX流体分析 HFSS电磁分析 Abaqus培训






