搜索关于动力学分析概述清单
2017-09-25 by:CAE仿真在线 来源:互联网
引言
什么是动力学分析?
动力学分析是用来确定惯性(质量效应)和阻尼起着重要作用时结构或构件动力学特性的技术。
“动力学特性” 可能指的是下面的一种或几种类型:
振动特性(结构振动方式和振动频率)
随时间变化载荷的效应(例如:对结构位移和应力的效应)
周期(振动)或随机载荷的效应
1、动力学分析通常分析下列物理现象:
振动 - 如由于旋转机械引起的振动
冲击 - 如汽车碰撞,锤击
交变作用力 - 如各种曲轴以及其它回转机械等
地震载荷 - 如地震,冲击波等
随机振动 - 如火箭发射,道路运输等
上述每一种情况都由一个特定的动力学分析类型来处理
2、例子:
1)在工作中,汽车尾气排气管装配体的固有频率与发动机的固有频率相同时,就可能会被震散。那么,怎样才能避免这种结果呢?
受应力(或离心力)作用的涡轮叶片会表现出不同的动力学特性,如何解释这种现象呢?
答案:进行 模态分析 来确定结构的振动特性
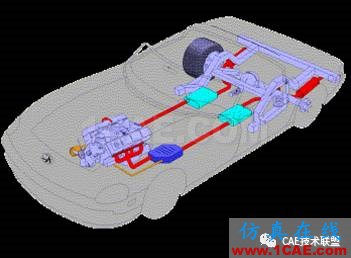
2)汽车防撞挡板应能承受得住低速冲击
一个网球排框架应该设计得能承受网球的冲击,但会稍稍发生弯曲
解决办法 :进行 瞬态动力学分析来计算结构对随时间变化载荷的响应
3)回转机器对轴承和支撑结构施加稳态的、交变的作用力,这些作用力随着旋转速度的不同会引起不同的偏转和应力
解决办法 : 进行谐分析来确定结构对稳态简谐载荷的响应
4)位于地震多发区的房屋框架和桥梁应该设计能够承受地震载荷要求。
解决办法:进行谱分析来确定结构对地震载荷的影响
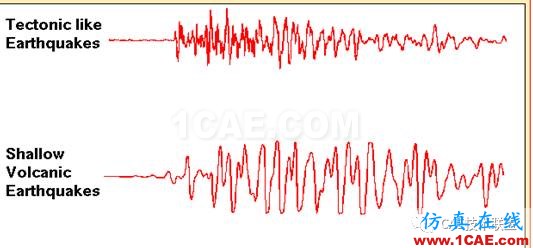
5)太空船和飞机的部件必须能够承受持续一段时间的变频率随机载荷。
解决办法 :进行随机振动分析来确定结构对随机震动的影响。
3、通用运动方程如下:
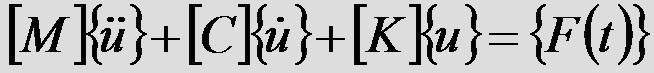不同分析类型是对这个方程的不同形式进行求解
模态分析:设定F(t)为零 ,而矩阵 [C] 通常被忽略;
谐响应分析:假设F(t) 和 u(t) 都为谐函数,例如 Xsin(wt),其中,X 是振幅, w 是单位为弧度/秒的频率;
瞬间动态分析:方程保持上述的形式。
其中:
[M] =结构质量矩阵
[C] =结构阻尼矩阵
[K] =结构刚度矩阵
{F} =随时间变化的载荷函数
{u} =节点位移矢量
{ } = 节点速度矢量
{ü} = 节点加速度矢量
4、如何求解通用运动方程 ?
两种主要方法:
模态叠加法
直接积分法
模态叠加法
按自然频率和模态将完全耦合的通用运动方程转化为一组独立的非耦合方程。
可以用来处理瞬态动力学分析和谐响应分析。
直接积分法
直接求解运动方程
在谐响应分析中,因为载荷和响应都假定为谐函数,所以运动方程是以干扰力频率的函数而不是时间的函数的形式写出并求解的。
对于瞬态动力学,运动方程保持为时间的函数,并且可以通过显式或隐式的方法求解。
5、建模要考虑的问题
材料性质:
需要定义杨氏模量和密度•请记住要使用一致的单位•当使用英制单位时,对于密度,要定义质量密度而不是重力密度:
质量密度=重力密度(lb/in3) / g (in/sec2)
钢的密度 = 0283/386 = 73 x 10-4 lb-sec2/in4
6、什么是阻尼?
阻尼是一种能量耗散机制,它使振动随时间减弱并最终停止
阻尼的数值主要取决于材料、运动速度和振动频率
阻尼可分类如下:
粘性阻尼
滞后或固体阻尼
库仑或干摩擦阻尼
相关标签搜索：关于动力学分析概述清单 Ansys有限元培训 Ansys workbench培训 ansys视频教程 ansys workbench教程 ansys APDL经典教程 ansys资料下载 ansys技术咨询 ansys基础知识 ansys代做 Fluent、CFX流体分析 HFSS电磁分析 Abaqus培训
