基于ANSYS的钢筋混泥土复合墙板力学性能分析
2017-11-02 by:CAE仿真在线 来源:互联网
复合墙板作为建筑结构中的主要保护构件,既要承担载荷的作用,还要阻隔室内室外的热交换。研发墙体的力学性能以及热工性能,可为墙板的设计应用提供有力的依据。本文在基于前章对墙板热学性能模拟分析的基础上,采用ANSYS有限元分析软件对墙板的力学性能进行模拟分析。
本文的模型采用的为夹心墙体,单元采用固体单元和梁单元,材料选用混泥土和钢筋材料,得到了夹心墙体力与位移载荷的曲线,同时得到极限抗弯强度。
一、模型的处理方式
ANSYS中对钢筋混凝土墙板模型的处理方式主要分为两种:分离式和分布式。分离式模型主要考虑钢筋和混凝土之间的粘结和滑移;而分布式假定混凝土和钢筋粘结很好,钢筋在混泥土中均匀分布。混泥土单元一般采用SOLID65单元,可以定义实常数R,来定义配筋的材料以及配筋的参数,如:体积率、方向角等。分离式模型需要用到link单元或者beam单元,link单元不能承受弯曲,而beam单元可以承受弯曲。应根据实际情况选择合理的单元。
本文选用的是分离式混泥土模型,采用SOLID65+beam188单元进行模拟。模型的建立效果如下图1所示。为了方便对模型进行网格的划分和载荷的施加,我们对模型进行了不同位置处的切割。
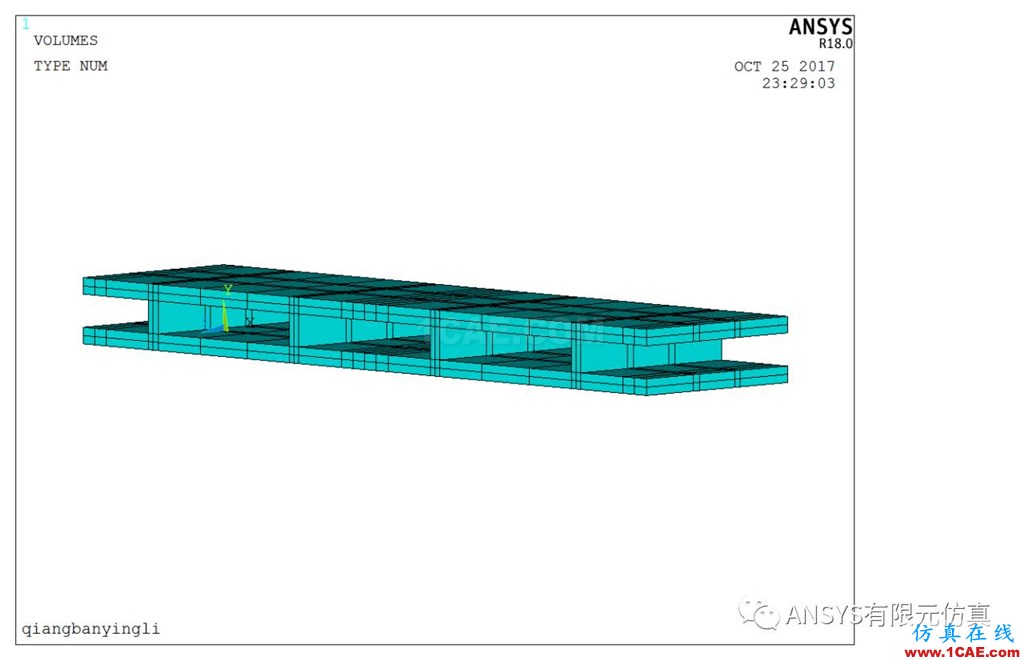
图1 复合墙板的有限元模型
二、网格的划分
混凝土的本构关系可以分为线弹性、非线性弹性、弹塑性及其它力学理论等四类,其中研究最多的是非线性弹性和弹塑性本构关系,其中不乏实用者。采用tb,concr,matnum则定义了W-W破坏准则(failure criterion),而非屈服准则(yield criterion)。定义tb,concr一般需要定义四个参数,分别为开口剪力传递系数(一般设为0.3~0.5)、闭口剪力传递系数(一般设为0.9~1)、单轴抗拉强度以及单轴抗压强度。
W-W破坏准则是用于检查混凝土开裂和压碎用的,混凝土的塑性可以另外考虑,当然塑性是在开裂和压碎之前,因为在材料破坏前才具有塑性。定义tb,concr matnum后仅仅是定义了混凝土的破坏准则和默认的本构关系,即W—W破坏准则(即混凝土开裂和压碎前均为线性的应力应变关系,而开裂和压碎后采用其给出的本构关系)。屈服准则可另外定义,随材料的应力应变关系,在ANSYS里面有双线性随动强化模型、多线性随动强化模型,双线性等效强化模型、多线性等效强化模型。
本文混泥土的屈服准则选用的是多线性随动强化模型,定义了混泥土模型的应力应变曲线;而钢筋的屈服准则选用的是双线性随动强化模型。混泥土的应力应变曲线如图2所示。
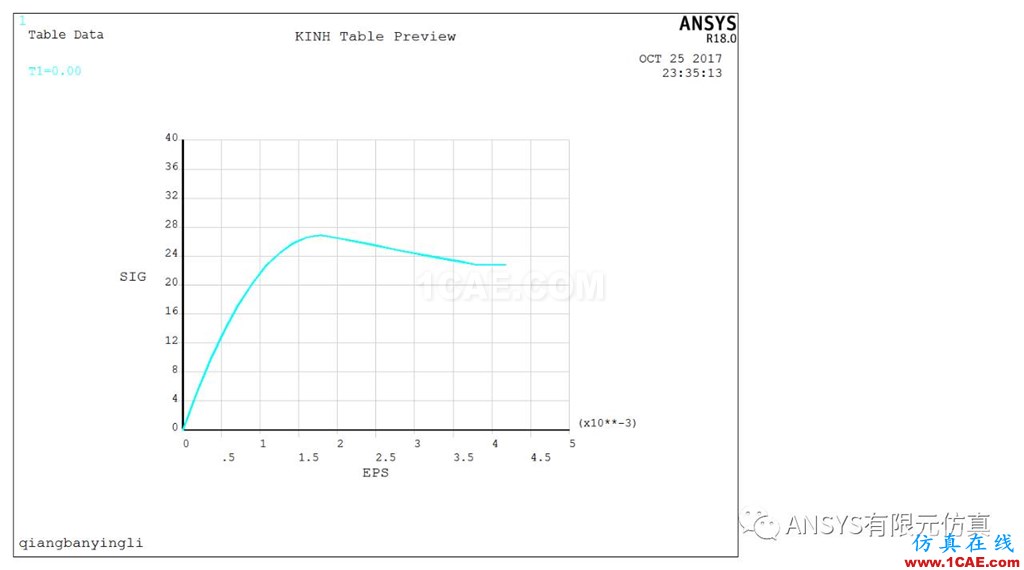
图2 混泥土多线性随动强化模型应力-应变曲线
网格的划分中,如果是分离式模型,则混泥土节点需要与钢筋节点采用耦合,或者利用相同的节点方式进行连接。考虑到收敛问题,一般混泥土的网格尺寸不应小于5mm。
本文采用共用节点的方式进行solid65单元和beam188单元的划分,beam188单元在定义的时候需要定义实常数,即梁单元横截面相关的几何参数。Solid65单元采用六面体网格化分方法,划分时单元尺寸设置为30mm,网格划分效果如下图3所示。
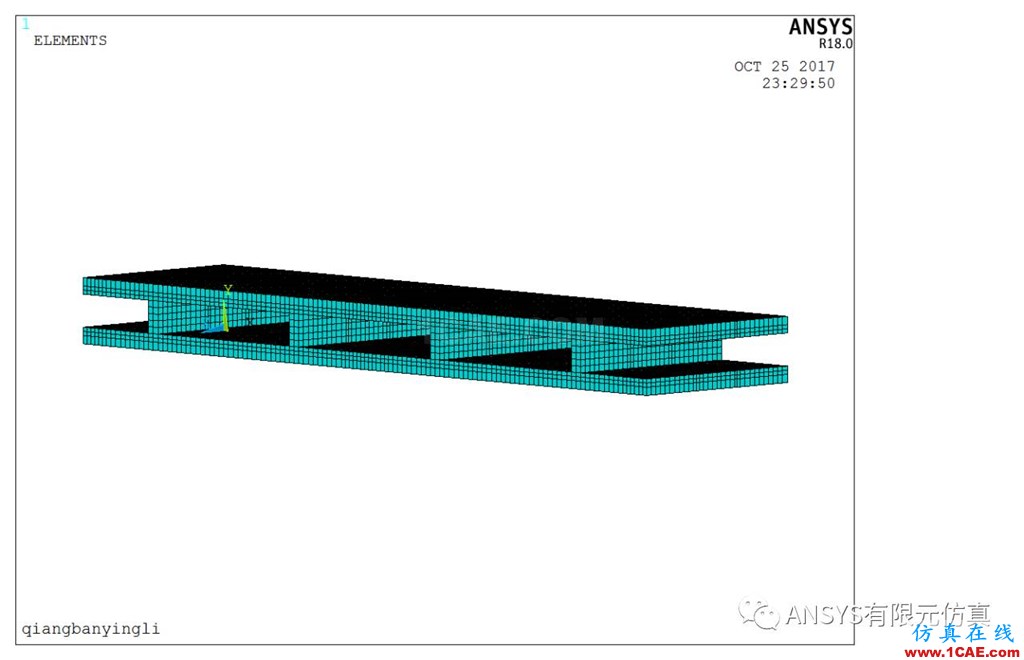
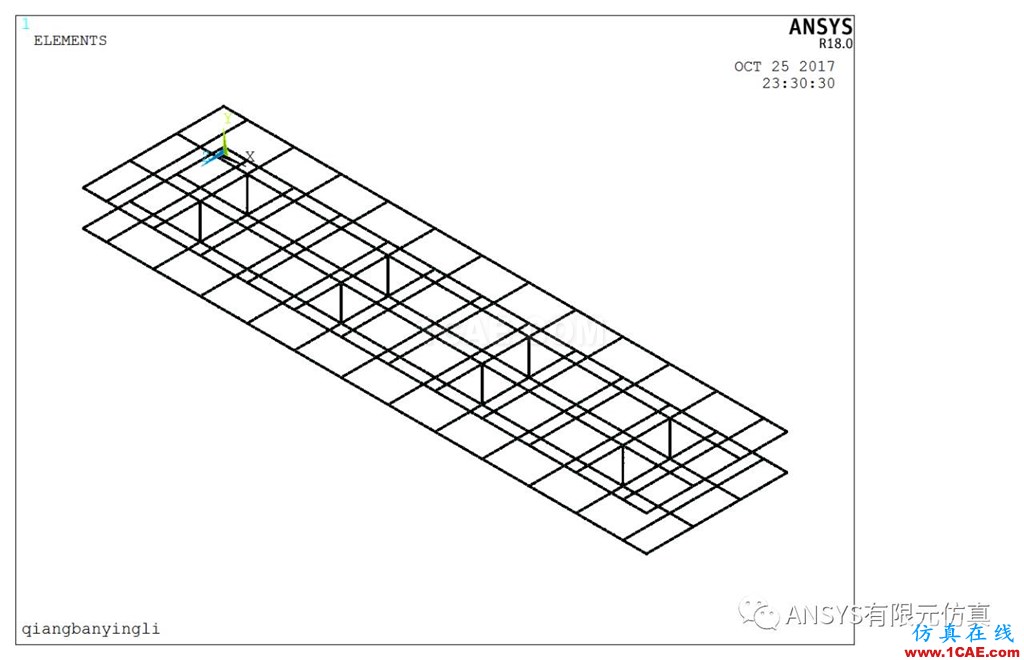
图3 网格划分示意图 (a)solid65单元(b)beam188单元
三、载荷的加载
对于ANSYS求混泥土的极限载荷有两种加载方式:
-
力加载:通过对应的方法(比如特征值屈曲)估计结构的极限载荷的大致范围,然后给结构施加一个稍大的载荷,打开自动载荷步二分法进行非线性静力分析,最后计算会因不收敛而终止,则倒数第二个子步对应的就是结构的极限载荷;另外也可以采用弧长法,采用足够的步数(弧长法一直可以分析到极限载荷承载力之后的过程)同样可以从绘制的载荷位移曲线或计算结果中找出结构的极限载荷。
-
位移加载:给结构施加一个大的位移,打开自动载荷步二分法进行非线性分析,保证足够的子步数,这样也可以通过绘制载荷位移曲线或者查看相应结果文件知道结构的极限载荷。
本文采用位移加载的方式。相对于力加载,位移加载在求解速度上更有优势。原因如下:涉及到塑性求解时,有材料的应力——应变曲线可知,材料的弹性模量不是定值,每一步求解中的材料弹性模量利用的是上一步的弹性模量值,而加载力之后,根据上一次的弹性模量求位移,进而求得应变,根据材料的应力-应变曲线,得到材料此位移下材料的真实弹性模型,与上一步的弹性模量指进行对比,进而更新第一次用的弹性模量,反复更新才能计算收敛。而位移加载,直接算得应变,根据材料的应力-应变曲线,可得到弹性模量,进而得到力,不用反复更新弹性模量,求解效率大大提高。
本文采用第二种求解方式,在复合墙板的正中加一个大的位移,根据底部固定节点的反力从而得到加载复合墙板上的载荷,同时利用acel命令流对钢筋混泥土的重量进行加载。相应的加载曲线如下图4所示。
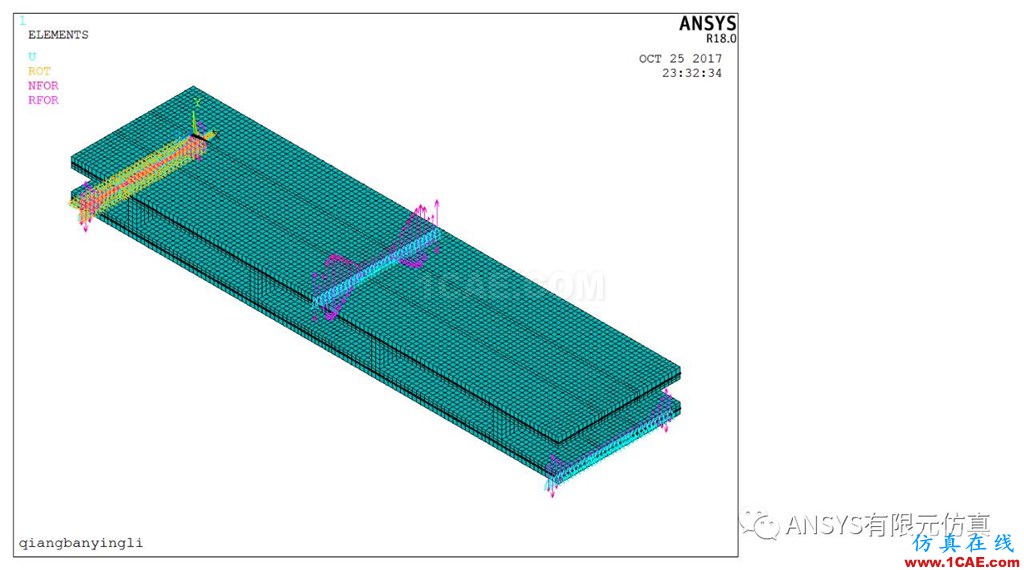
图4 墙板的位移加载示意图
四、求解器的控制
ANSYS混泥土的非线性计算收敛是非常困难的。主要影响因素有网格密度、子步数、收敛准则等。
-
网格密度:网格密度适当能够收敛。不是网格越密越好,当然太稀疏也不行,这仅仅是就收敛而言的,不考虑计算时间问题。但是究竟多少合适,没有找到规律,只能靠自己针对情况慢慢调试。
-
子步数:NSUBST的设置很重要,设置太大或太小都不能达到正常收敛。这点可以从收敛过程图看出,如果F范数曲线在[F]曲线上面走形的很长,可考虑增大nsubst。或者根据经验慢慢调正试算。
-
收敛精度:实际上收敛精度的调正并不能彻底解决收敛的问题,但可以放宽收敛条件以加速收敛。一般工程引用为不超过5%(默认是0.5%),且使用力收敛条件即可。我们看到求解时ANSYS求解结果的曲线一个是收敛准则(通常为F、U、M),另外一个是相应计算出来用以和收敛准则进行比较的结果值。其中用以比较的为F矩阵的2阶范数(默认)、U矩阵的无穷大范数(默认)、M矩阵的2阶范数(默认)。关于矩阵范数的概念,在研究生的数值计算中会讲到,当所有求解结果相应的范数小于收敛准则时,Ansys认为结果有效,从而进行下一步的求解。可以使用CNVTO来改变相应的收敛准则。
-
混凝土压碎的设置:不考虑压碎时,计算相对容易收敛;而考虑压碎则比较难收敛,即便是没有达到压碎应力时。如果是正常使用情况下的计算,建议关掉压碎选项;如果是极限计算,建议使用concr+MISO且关闭压碎检查;如果必设压碎检查,则要通过大量的试算(设置不同的网格密度、NSUBST)以达到目的,但也很困难。
-
其他选项:如线性搜索、预测等项也可以打开,以加速收敛,但不能根本解决问题。
本文在求解器的控制中打开了大变形选型、预测选项、位移、力、力矩的收敛准则为5%,平均子步数为200。
五、结果的分析
模型的载荷—位移曲线如下图5所示。由图5可知,在变形量为0~0.489mm时,模型所受的力随位移的增大而增大,当位移为0.48891mm时,载荷达到最大为2.538kn,而后随着位移的增大,力迅速下降,后随着位移的增大力缓慢上升。可知,在位移为0.489mm时,混泥土发生断裂,因为当混泥土发生断裂的时候,力会随着位移的上升而突然下降。此时承受的力为2.538kn,即模型能承受的极限载荷为2.538kn。
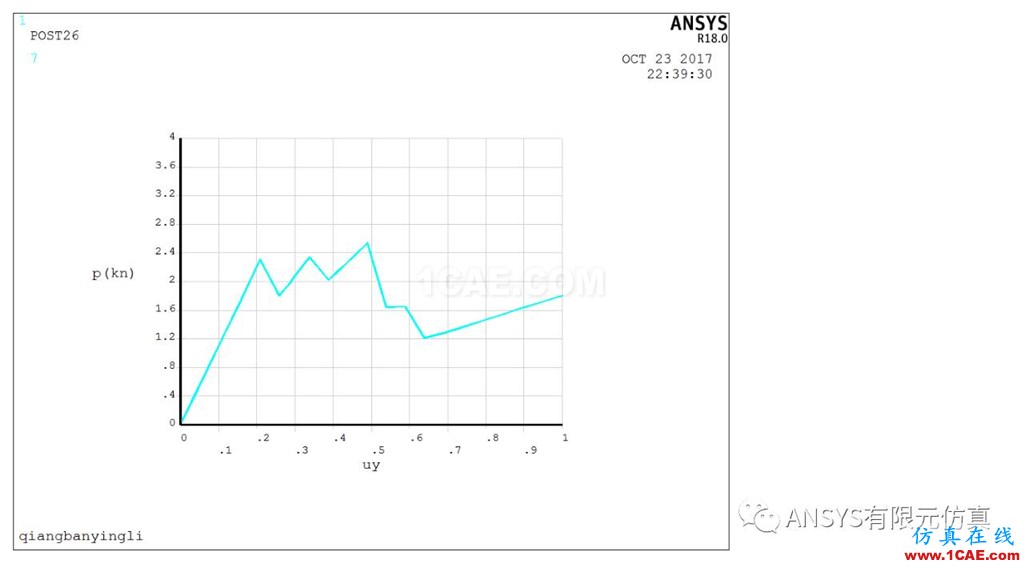
图5 墙板的载荷和位移曲线图
另外一种采用力加载的方式,求得的极限载荷为2.6kn,和位移加载的方式相差在2.4%。充分证明了两种加载方式的正确性和合理性。


图6 极限载荷下模型的等效位移和等效应力示意图(a)等效位移(b)等效应力
在相应的位移下,模型的等效变形量和等效应力分别如下图6(a)、(b)所示。
相关标签搜索:基于ANSYS的钢筋混泥土复合墙板力学性能分析 Ansys有限元培训 Ansys workbench培训 ansys视频教程 ansys workbench教程 ansys APDL经典教程 ansys资料下载 ansys技术咨询 ansys基础知识 ansys代做 Fluent、CFX流体分析 HFSS电磁分析 Abaqus培训






