Abaqus有限单元——单元的表征

2013-08-14 by:Abaqus非线性来源:仿真在线

Abaqus有限单元——单元的表征

ABAQUS提供了广泛的单元,其庞大的单元库为你提供了一套强有力的工具以解决多种不同类型的问题。在ABAQUS/Explicit中的单元是在ABAQUS/Standard中的单元的一个子集。本节将介绍影响每个单元特性的五个方面问题。

3.1.1 单元的表征

每一个单元表征如下:

l 单元族

l 自由度(与单元族直接相关)

l 节点数目

l 数学描述

l 积分

ABAQUS中每一个单元都有唯一的名字,例如T2D2,S4R或者C3D8I。单元的名字标识了一个单元的五个方面问题的每一个特征。命名的约定将在本章中说明。

单元族

图3-1给出了应力分析中最常用的单元族。在单元族之间一个主要的区别是每一个单元族所假定的几何类型不同。

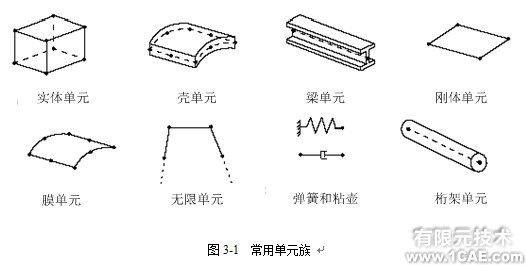
Abaqus有限单元——单元的表征ansys分析图片1

在本指南中将用到的单元族有实体单元、壳单元、梁单元、桁架和刚性体单元,这些单元将在其它章节里详细讨论。本指南没有涉及到的单元族;读者若在模型中对应用它们感兴趣,请查阅ABAQUS分析用户手册的第V部分“Elements”。

一个单元名字第一个字母或者字母串表示该单元属于哪一个单元族。例如,S4R中的S表示它是壳(shell)单元,而C3D8I中的C表示它是实体(contimuum)单元。

自由度

自由度(dof)是在分析中计算的基本变量。对于应力/位移模拟,自由度是在每一节点处的平动。某些单元族,诸如梁和壳单元族,还包括转动的自由度。对于热传导模拟,自由度是在每一节点处的温度;因此,热传导分析要求使用与应力分析不同的单元,因为它们的自由度不同。

在ABAQUS中使用的关于自由度的顺序约定如下:

1 1方向的平动

2 2方向的平动

3 3方向的平动

4 绕1轴的转动

5 绕2轴的转动

6 绕3轴的转动

7 开口截面梁单元的翘曲

8 声压、孔隙压力或静水压力

9 电势

11 对于实体单元的温度(或质量扩散分析中的归一化浓度),或者在梁和壳的厚度上第一点的温度

12+ 在梁和壳厚度上其它点的温度(继续增加自由度)

除非在节点处已经定义了局部坐标系,方向1、2和3分别对应于整体坐标的1-、2- 和3-方向。

轴对称单元是一个例外,其位移和旋转的自由度规定如下:

1 r-方向的平动

2 z-方向的平动

6 r-z平面内的转动

除非在节点处已经定义了局部坐标系,方向r(径向)和z(轴向)分别对应于整体坐标的1-和2-方向。关于在节点处定义局部坐标系的讨论,见第5章“应用壳单元”。

在本指南中我们注意力限于结构应用方面,所以只讨论具有平动和转动自由度的单元。关于其它类型的单元的信息(如热传导单元),可参考ABAQUS分析用户手册。

节点数目—插值的阶数

ABAQUS仅在单元的节点处计算前面提到的位移、转动、温度和其它自由度。在单元内的任何其它点处的位移是由节点位移插值获得的。通常插值的阶数由单元采用的节点数目决定。

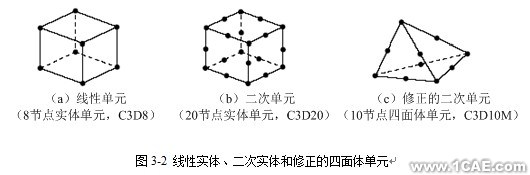
l 仅在角点处布置节点的单元,如图3-2(a)所示的8节点实体单元,在每一方向上采用线性插值,常常称它们为线性单元或一阶单元。

l 在每条边上有中间节点的单元,如图3-2(b)所示的20节点实体单元,采用二次插值,常常称它们为二次单元或二阶单元。

l 在每条边上有中间节点的的修正三角形或四面体单元,如图3-2(c)所示的10节点四面体单元,采用修正的二阶插值,常常称它们为修正的单元或修正的二阶单元。

Abaqus有限单元——单元的表征ansys分析图片2

ABAQUS/Standard提供了对于线性和二次单元的广泛的选择。除了二次梁单元和修正的四面体和三角形单元之外,ABAQUS/Explicit仅提供线性单元。

一般情况下,一个单元的节点数目清楚地标识在其名字中。8节点实体单元,如前面所见,称为C3D8;8节点一般壳单元称为S8R。梁单元族采用了稍有不同的约定:在单元的名字中标识了插值的阶数。这样,一阶三维梁单元称为B31,而二阶三维梁单元称为B32。对于轴对称壳单元和膜单元采用了类似的约定。

数学描述(Formulation)

单元的数学描述是指用来定义单元行为的数学理论。在不考虑自适应网格(adaptive meshing)的情况下,在ABAQUS中所有的应力/位移单元的行为都是基于拉格朗日(Lagrangian)或材料(material)描述:在分析中,与单元关联的材料保持与单元关联,并且材料不能从单元中流出和越过单元的边界。与此相反,欧拉(Eulerian)或空间(Spatial)描述则是单元在空间固定,材料在它们之间流动。欧拉方法通常用于流体力学模拟。ABAQUS/Standard应用欧拉单元模拟对流换热。在ABAUQS/Explicit中的自适应网格技术,与纯拉格朗日和欧拉分析的特点组合,它允许单元的运动独立于材料。在本指南中不讨论欧拉单元和自适应网格技术。

为了适用于不同类型的行为,在ABAQUS中的某些单元族包含了几种采用不同数学描述的单元。例如,壳单元族具有三种类型:一种适用于一般性目的的壳体分析,另一种适用于薄壳,余下的一种适用于厚壳。(这些壳单元的数学描述将在第5章“应用壳单元”中给予解释)。

ABAQUS/Standard的某些单元族除了具有标准的数学公式描述外,还有一些其它可供选择的公式描述。具有其它可供选择的公式描述的单元由在单元名字末尾的附加字母来识别。例如,实体、梁和桁架单元族包括了采用杂交公式的单元,它们将静水压力(实体单元)或轴力(梁和桁架单元)处理为一个附加的未知量;这些杂交单元由其名字末尾的“H”字母标识(C3D8H或B31H)。

有些单元的数学公式允许耦合场问题求解。例如,以字母C开头和字母T结尾的单元(如C3D8T)具有力学和热学的自由度,可用于模拟热-力耦合问题。

几种最常用的单元数学描述将在本指南的后面章节中讨论。

积分

ABAQUS应用数值方法对各种变量在整个单元体内进行积分。对于大部分单元,ABAQUS运用高斯积分方法来计算每一单元内每一个积分点处的材料响应。对于ABAQUS中的一些实体单元,可以选择应用完全积分或者减缩积分,对于一个给定的问题,这种选择对于单元的精度有着明显的影响,如在第4.1节“单元的数学描述和积分”中所详细讨论的。

ABAQUS在单元名字末尾采用字母“R”来标识减缩积分单元(如果一个减缩积分单元同时又是杂交单元,末尾字母为RH)。例如,CAX4是4节点、完全积分、线性、轴对称实体单元;而CAX4R是同类单元的减缩积分形式。

ABAQUS/Standard提供了完全积分和减缩积分单元;除了修正的四面体和三角形单元外,ABAQUS/Explicit只提供了减缩积分单元。

开放分享：优质有限元技术文章,助你自学成才