Abaqus教程——实体单元
2013-08-14 by:Abaqus软件应用培训中心 来源:仿真在线
Abaqus教程——实体单元
在不同的单元族中,连续体或者实体单元能够用来模拟范围最广泛的构件。顾名思义,实体单元简单地模拟部件中的一小块材料。由于它们可以通过其任何一个表面与其它单元相连,实体单元就像建筑物中的砖或马赛克中的瓷砖一样,因此能够用来构建具有几乎任何形状、承受几乎任意载荷的模型。ABAQUS具有应力/位移和热-力耦合的实体单元;本指南中将只讨论应力/位移单元。
在ABAQUS中,应力/位移实体单元的名字以字母“C”开头。随后的两个字母一般(并不总是)表示维数,即单元的有效自由度数目。字母“3D”表示三维单元;“AX”,表示轴对称单元;“PE”,表示平面应变单元;而“PS”,表示平面应力单元。
在第四章“应用实体单元”中,将对应用实体单元展开进一步的讨论。
三维实体单元库
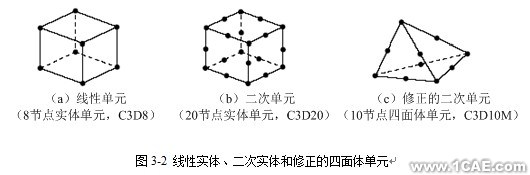
三维实体单元可以是六面体形(砖形)、楔形或四面体形。关于三维实体单元的详细目录和每种单元中节点的连接方式,请参阅ABAQUS分析用户手册的第14.1.4节“Three-dimensional solid element library”。
在ABAQUS中,应尽可能地使用六面体单元或二阶修正的四面体单元。一阶四面体单元(C3D4)具有简单的的常应变公式,为了得到精确的解答需要非常细划的网格。
二维实体单元库
ABAQUS拥有几种离面行为互不相同的二维实体单元。二维单元可以是四边形或三角形。应用最普遍的三种二维单元如图3-3所示。
平面应变(plain strain)单元假设离面应变为零;它们可以用来模拟厚结构。
平面应力(plain stress)单元假设离面应力为零;这类单元适合于用来模拟薄结构。
无扭曲的轴对称单元,CAX类单元,可模拟360°的环;它们适合于分析具有轴对称几何形状和承受轴对称荷载的结构。
ABAQUS/Standard也提供了广义平面应变单元、可以扭曲的轴对称单元和具有反对称变形的轴对称单元。
l 广义平面应变单元包含了对原单元的推广,即离面应变可以随着模型平面内的位置发生线性变化。这种单元列式特别适合于厚截面的热应力分析。
l 带有扭曲的轴对称单元可以模拟初始时为轴对称几何形状,但能沿对称轴发生扭曲的模型。它们适合于模拟圆桶形结构的扭转,如轴对称的橡胶套管。
l 带有反对称变形的轴对称单元可以模拟初始时为轴对称几何形状,但能反对称变形的物体(特别是作为弯曲的结果)。它们适合于模拟诸如承受剪切载荷的轴对称橡胶支座的问题。
在这本指南中不讨论上面提到的这三种二维实体单元。
二维实体单元必须在1-2平面内定义,并使节点编号顺序绕单元周界是逆时针的,如图3-4所示。
当使用前处理器生成网格时,要确保所有点处的单元法线沿着同一方向,即正向,沿着整体坐标的3轴。不能提供正确的单元节点布局将引起ABAQUS给出单元具有负面积的出错信息。
自由度
所有的应力/位移实体单元在每一节点处有平动自由度。相应的在三维单元中,自由度1、2和3是有效的,而在平面应变单元、平面应力单元和无扭曲的轴对称单元中,只有自由度1和2是有效的。关于其它类型的二维实体单元的有效自由度,请参阅ABAQUS分析用户手册的第14.1.3节“Two-dimensional solid element library”。
单元性质
所有的实体单元必须赋予截面性质,它定义了与单元相关的材料和任何附加的几何数据。对于三维和轴对称单元不需要附加几何信息:节点坐标就能够完整地定义单元的几何形状。对于平面应力和平面应变单元,可能要指定单元的厚度,或者采用为1的默认值。
数学描述和积分
在ABAQUS/Standard中,关于实体单元族有可供选择的数学描述,包括非协调模式(incompatible mode)的数学描述(在单元名字的最后一个或倒数第二个字母为I)和杂交单元的数学描述(单元名字的最后一个字母为H),在本指南的后面章节中将详细讨论它们。
在ABAQUS/Standard中,对于四边形或六面体(砖形)单元,可以在完全积分和减缩积分之间进行选择。在ABAQUS/Explicit中,只能使用减缩积分的四边形或六面体实体单元。数学描述和积分方式都会对实体单元的精度产生显著的影响。如在第4.1节“单元的数学描述和积分”中所讨论的。
单元输出变量
默认情况下,诸如应力和应变等单元输出变量都是参照整体笛卡尔直角坐标系的。因此,在积分点处应力分量是作用在整体坐标系的1方向,如图3-5(a)所示。即使在一个大位移模拟中单元发生了转动,如图3-5(b)所示,仍默认是在整体笛卡尔坐标系中定义单元变量。
然而,ABAQUS允许用户为单元变量定义一个局部坐标系(见第5.5节“例题:斜板”)。该局部坐标系在大位移模拟中随着单元的运动而转动。当所分析的物体具有某个自然材料方向时,如在复合材料中的纤维方向,局部坐标系将会是十分有用的。
相关标签搜索:Abaqus教程——实体单元 广州Abaqus分析培训 Abaqus接触分析教程 Ansys有限元培训 Ansys workbench培训 ansys视频教程 ansys workbench教程 ansys APDL经典教程 ansys资料下载 ansys技术咨询 ansys基础知识 ansys代做 Fluent、CFX流体分析






