Abaqus有限元分析实例解析——在棒中的应力波传播(三)
2013-08-14 by:有限元软件应用培训中心 来源:仿真在线
Abaqus有限元分析实例解析——在棒中的应力波传播(三)
9.4.3 网格对稳定时间增量和CPU时间的影响
在第9.3节“自动时间增量和稳定性”中,我们讨论过网格细划对稳定极限和CPU时间的影响。这里我们将以波的传播问题来说明这一影响。我们从方形单元的一种合理的精细网格开始,沿长度方向划分50个单元,两个横向方向各划分10个单元。为了说明问题,我们现在采用一种25×5×5单元的粗糙网格,并观察在各种方向上如何细划网格改变CPU时间。四种网格如图9-11所示。
表9-1显示了本问题的CPU时间随着网格细划的改变(以粗糙网格的模型结果进行了单位化)。基于在本指南中介绍的简单的稳定性方程,表格的前一半提供了期望值;表格的后一半给出了在计算机工作站上由ABAQUS/Explicit运行分析得到的结果。
表 9-1 网格细划和求解时间
|
网格 |
简化理论 |
实际 |
||||
|
|
(秒) |
单元数 |
CPU时间(秒) |
最大(秒) |
单元数 |
CPU时间(秒) |
|
25×5×5 |
A |
B |
C |
6.06e-6 |
625 |
1 |
|
50×5×5 |
A/2 |
2B |
4C |
3.14e-6 |
1250 |
4 |
|
50×10×5 |
A/2 |
4B |
8C |
3.12e-6 |
2500 |
8.33 |
|
50×10×10 |
A/2 |
8B |
16C |
3.11e-6 |
5000 |
16.67 |
对于理论解答,我们选择25×5×5的最粗糙网格作为基本状态,并且定义稳定的时间增量、单元数量和CPU时间分别为变量A、B和C。随着网格的细划,产生了两种结果:最小的单元尺寸减小了,以及在网格中的单元数目增加了,这些影响的每一种都会增加CPU时间。在第一次细划的50×5×5网格中,最小单元的尺寸减小了一半,并且单元的数目增加了一倍,因此增加了CPU时间,使其是前一种网格的四倍。然而,进一步加倍网格数目至50×10×5,没有改变最小单元的尺寸;而仅仅是加倍了单元数量。因此,CPU时间是50×5×5网格的二倍。进一步地细划网格为50×10×10,使单元成为均匀的方形,再一次加倍了单元的数量和CPU时间。
这种简单的计算非常好地预测了网格细划如何影响稳定时间增量和CPU时间的趋势。然而,为什么我们没有将预测值与实际的稳定时间增量值进行比较?这里是有原因的。首先回忆一下我们给出的稳定时间增量的近似公式为

然后我们假定单元特征长度是最小的单元尺寸,而ABAQUS/Explicit实际上是根据单元的整体尺寸和形状来确定单元特征长度的。另外一个因素是ABAQUS/Explicit采用了一个整体稳定性估算,它允许使用一个更大的稳定时间增量。这些因素使得在运行分析之前实际上难以准确地预测稳定时间增量。然而,由于预测的趋势与简单的理论符合得很好,因此可以直接地预测稳定时间增量如何随着网格细划而发生变化。
9.4.4 材料对稳定时间增量和CPU时间的影响
同样的波扩展分析在不同的材料中进行将需要不同的CPU时间,这取决于材料的波速。例如,如果我们改变材料从钢到铝,波速将从5.15×103 m/s变成为
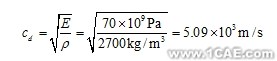
因为刚度和密度几乎改变了相同的量级,所以从铝到钢对稳定时间增量只有微小的影响。在铅的情况下,差别则变得非常大,其波速减小为

这个值大约是钢的波速的五分之一。铅棒的稳定时间增量将是钢棒的稳定时间增量的五倍。
相关标签搜索:Abaqus有限元分析实例解析——在棒中的应力波传播(三) 广州有限元课程 Abaqus分析 有限元设计仿真 Ansys有限元培训 Ansys workbench培训 ansys视频教程 ansys workbench教程 ansys APDL经典教程 ansys资料下载 ansys技术咨询 ansys基础知识 ansys代做






