流固耦合的学特性分析
2013-06-20 by:广州有限元分析、培训中心-1CAE.COM 来源:仿真在线
在大型液体火箭中,经常会采用金属膜盒进行动密封和吸收管路系统脉动压力等。虽然金属膜盒在航天中应用较多,但由于其结构和所处环境的复杂性,在理论分析方面仍旧在探索阶段。本文所研究的金属膜盒,型面为锯齿型,其内部充有一定压力的气体,外部承受一定压力的水压。文中在充分考虑膜盒跟外界液体的流固耦合基础上,用ANSYS软件对该金属膜盒进行了特定状态下的动力学特性分析,并与试验数据进行了对比,结果较为接近。
宇航系统工程研究所 史淑娟 朱礼文 赫崇智 蔡鹏 来源:e-works
关键字:充压膜盒 流固耦合 动力学特性
1 前言
本文主要对内部充气,外部充液的金属膜盒进行了动力学特性分析,为火箭动力系统的设计提高必要的参考依据。在文中,主要利用ANSYS软件的流固耦合分析,进行了该金属膜盒的动力学特性分析。
2 问题简介
金属膜盒内部分别充一定压力的压缩空气,外部分别充一定压力的水压,膜盒的底盘固定,金属膜盒的结构原理图和所处状态见图1。文中主要针对该种状态的膜盒进行动力学特性的求解。
图1金属膜盒结构原理
3 求解模型的建立
3.1 简化与假设
在进行充压金属膜盒的动力学特性求解前,首先做如下的假设:
由于膜盒的机械变形对内部充气压的金属膜盒系统的刚度影响不大,故计算中忽略膜盒本身的机械刚度。
认为膜盒内气体遵循理想气体状态方程
认为流体不可压
3.2 问题分析
由于该金属膜盒结构和所处环境较为复杂,故在建立模型前,对膜盒内部气体和膜盒外部液体的作用进行了简单分析,以进行模型的最终建立。
金属膜盒气体对膜盒系统的刚度影响很大,由此密闭气体将对膜盒的固有频率产生较大的影响,但是当外部液压加在膜盒上时,密闭气体的刚度将随膜盒容积的变化而变化,它在容积变化中显示出的非线性刚度是不能够为动力学特性求解所包括的。模态分析是线性系统的特征量,如果一个非线性系统可以以某种方式进行线性化,所得到的线性化系统的模态参数能代表非线性系统的某些重要特征,那么,这种模态分析还是有意义的,假设在压力平衡后膜盒内部气体的容积不发生变化,故可以用该压力点处的气体等效切线刚度进行求解。具体等效刚度的求解在本文中不予介绍。
膜盒外部的液体在计算充压膜盒的动力学特性中主要起液阻的作用,当充液膜盒振动时必将诱导周围流体的运动,而流体对膜盒结构的反作用又施加到结构表面,影响膜盒的振动特性。所以膜盒的动力学特性求解问题是一个实际中需要加以解决的流固耦合问题。在ANSYS的流固耦合场分析问题上有两种方法可供选择:序贯耦合方法和直接耦合方法。由于序贯法需要多次重启动反复计算流体场的荷载,而模态分析无法进行重启动且不能够包括不断变化的外载荷的作用,另外文中只考虑了流体的静压作用,所以采用直接法进行求解。具体可以通过施加FSI标记子而将流体的压力和固体的变形直接联系起来进行求解。另外在ANSYS中可以进行考虑流固耦合的模态求解。
3.3 有限元模型的建立
3.3.1 三维几何模型的建立
虽然膜盒本身具有对称性,但考虑到蓄压器的模态中包含非对称模态,所以模型采用三维实体模型。首先分别对金属膜盒的膜片组、上盖、外筒和膜盒周围的液体以及膜盒上部的特定高度液体(通道到上盖间的那部分液体)进行几何模型的建立,建立的几何模型的截面见图2。
3.3.1.1 单元的选择
在金属膜盒的动力学特性计算中分别采用45号单元与30号声流-结构耦合单元进行结构和流体单元的离散;膜盒内部气体采用14号弹簧单元模拟其等效刚度;试验管路内的液体惯性采用液体附加质量法进行模拟,用21号质量单元离散。
30号三维声学流体单元用于模拟流体介质和流体/结构相互作用的界面。该单元有八个节点,每个节点有4个自由度:x、y、z方向的平动和压力。但只有在界面上的平动自由度(通过控制该单元的开关)才有效。下面是其单元的示意图:
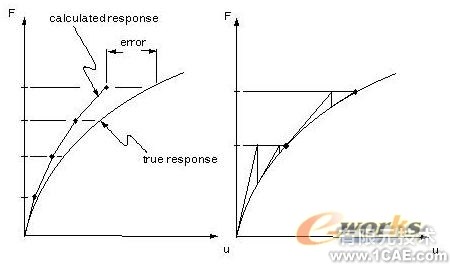
3.3.1.2 材料属性:
膜盒有限元离散的单元物理属性见下表1,膜盒内气体的等效刚度见表2。
表1 充压膜盒有限元单元物理属性
|
结构 |
离散单元 |
弹性模量(pa) |
密度(㎏/m3) |
声速(m/s) |
|
膜片 |
45号实体单元(共17344个) |
2e11 |
7800 |
|
|
上盖 |
7500 | |||
|
与固体接触的流体 |
30号流固耦合单元(6816个) |
2e9 |
1000 |
1414 |
|
不与固体接触的流体 |
30号流固耦合单元(4048个) | |||
|
气体 |
14号弹簧单元(7个) |
K=见表2 | ||
|
液体等效质量 |
21号质量单元(1个) |
m=100Kg | ||
表2不同内压和外压下膜盒的等效气体刚度
|
膜盒内气压(MPa) |
低压 | ||
|
膜盒外液压(MPa) |
低压 |
中压 |
高压 |
|
膜盒高度(mm) |
28.36 |
25.4 |
0.0232 |
|
膜片高度(mm) |
0.709 |
0.63447 |
0.58054 |
|
膜盒等效刚度(N/m) |
6.3886e+004 |
5.8384e+004 |
5.4959e+004 |
|
膜盒内气压(MPa) |
高压 | ||
|
膜盒外液压(MPa |
低压 |
中压 |
高压 |
|
膜盒高度(mm) |
52.5 |
46.9 |
40.3 |
|
膜片高度(mm) |
1.3 |
1.2 |
1.0 |
|
膜盒等效刚度(N/m) |
4.9581e+005 |
2.8637e+005 |
1.8932e+005 |
3.3.1.3 边界条件
在模型中,采用膜盒底部固支,上部自由的边界处理。在流固耦合界面(即膜片和液体接触处以及外筒和液体接触处)加标记子FSI,从而使固体的位移和流体的压力在此耦合。
3.3.1.4 求解器
采用ANSYS的非对称(Unsymmetric)模态提取方法,在内存512MB,硬盘容量为20GB的计算机上用了三小时15分钟得到最后的结果,由于一阶频率比较低,而试验中得到的频率大多在20Hz左右,所以特计算了2阶频率以做参考。有限元模型见图4,结果见表3。
表3 采用三维有限元求解的膜盒固有频率
|
气压(MPa) |
液压(MPa) |
膜盒固有频率(Hz) |
振型描述 | |
|
P0=低压 |
P=低压 |
1 |
8.548 |
膜盒上下均匀振动周向波为零 |
|
2 |
17.628 |
轴向有一个疏密波周向波为零 | ||
|
P=中压 |
1 |
9.046 |
膜盒上下均匀振动周向波为零 | |
|
2 |
53.48 |
轴向有一个疏密波周向波为零 | ||
|
P=高压 |
1 |
8.408 |
膜盒上下均匀振动周向波为零 | |
|
2 |
52.153 |
轴向有一个疏密波周向波为零 | ||
|
P0=高压 |
P=低压 |
1 |
10.681 |
膜盒上下均匀振动周向波为零 |
|
2 |
45.131 |
轴向有一个疏密波周向波为零 | ||
|
P=中压 |
1 |
6.767 |
膜盒上下均匀振动周向波为零 | |
|
2 |
48.98 |
轴向有一个疏密波周向波为零 | ||
|
P=高压 |
1 |
7.3034 |
膜盒上下均匀振动周向波为零 | |
|
2 |
51.695 |
轴向有一个疏密波周向波为零 | ||
3.3.1.5.1试验状态介绍
膜盒的自振频率试验,是考虑在一定脉动压力下膜盒的响应方法实现的。考虑在一段流体的试验管路下,取单侧膜盒,另外一侧用堵盖封堵。试验图见图5。
3.3.1.5.2试验结果
试验通过振动台施加流体脉动后测得试验管路内的共振频率获得膜盒的自振频率,结果见表4。
表4充液膜盒的自振频率试验结果
|
膜盒内气压(MPa) |
低压 | ||
|
膜盒外液压(MPa) |
低压 |
中压 |
高压 |
|
自振频率(Hz) |
26.25 |
29 |
31.25 |
|
膜盒内气压(MPa) |
高压 | ||
|
膜盒外液压(MPa |
低压 |
中压 |
高压 |
|
自振频率(Hz) |
22.25 |
24.5 |
26.75 |
3.3.1.5.3结果分析
膜盒充水后,由于液体对膜盒系统质量、刚度和阻尼阵的影响,系统的固有频率将不同于不注水下的固有频率。三维实体模型与试验结果的对比见表5:
表5三维实体模型的充液膜盒固有频率对比
|
膜盒内气压(MPa) |
低压 | ||
|
膜盒外液压(MPa) |
低压 |
中压 |
高压 |
|
试验自振频率(Hz) |
26.25 |
29 |
31.25 |
|
采用实体单元的一阶结果(Hz) |
8.548 |
9.046 |
8.408 |
|
采用实体单元的二阶结果(Hz) |
17.628 |
53.48 |
52.153 |
|
膜盒内气压(MPa) |
高压 | ||
|
膜盒外液压(MPa) |
低压 |
中压 |
高压 |
|
自振频率(Hz) |
22.25 |
24.5 |
26.75 |
|
采用实体单元的一阶结果(Hz) |
10.681 |
6.767 |
7.303 |
|
采用实体单元的二阶结果(Hz) |
45.131 |
48.98 |
51.695 |
从结果的对比中可以看出,用实体单元进行求解的结果远远低于试验的结果。这一方面是由于直接耦合方法在处理流固耦合界面时将界面上的全部自由度均进行了耦合,即流体相对于固体不可以自由滑动,这使结果产生一定的误差;另一方面在试验过程中,由于试验管路布局的限制,造成试验管路中不可避免地产生一定量的空气,而在计算中没有考虑到这部分空气的影响,所以导致试验数据要比计算数据偏大。
虽然直接法的误差较大,但是它却可以了解膜盒在低频阶段的真实振型和在不同内外压下的规律。
3.3.2 轴对称模型
在三维模型中计算的一阶模态为上下振动,二级模态为呼吸振动,周向波均为0,在模态上均为对称形式,所以可以采用轴对称流体单元进行耦合分析,这样既可以了解流体对膜盒固有特性的影响,又可以大大缩减计算时间。
3.3.2.1 单元选择
固体用轴对称谐波单元shell61,流体用轴对称谐波封闭单元fluid81。fluid81是轴对称谐波封闭流体元,用于模拟装在容器内的无净流率的流体,该单元由四个节点定义,每个节点有三个自由度:x、y、z方向的平动。该单元特别适合于计算静水压力和流体与固体的相互作用。内部气体的等效刚度采用14号弹簧单元模拟。
3.3.2.2 材料属性
采用轴对称单元计算充液膜盒流固耦合动力学特性的单元与材料见表6。
表6轴对称单元与材料
|
结构 |
离散单元 |
弹性模量(pa) |
密度(㎏/m3) |
|
膜片 |
Shell61(680个) |
2e11 |
7500 |
|
导杆 |
Mass21(1个) |
包括导杆的质量 | |
|
上盖与外筒 |
Shell61(124个) |
2e11 |
7800 |
|
流体 |
Fluid81(927个) |
2e9 |
1000 |
|
内部气体 |
Combine14(7个) |
K=见表2 | |
流体与膜盒壳体接触的表面上法向位移协调,另外由于底盘不是主要振动部件,所以夹在底盘缝隙中的流体可以忽略不计。膜盒底部固定,上盖自由。
3.3.2.4 求解方法
采用模态提取方法中的缩减法进行求解,主自由度选取膜盒端面的流体自由度。在求解中根据平衡后的膜盒高度进行建模,即尽量使得刚度矩阵与实际状态接近。有限元模型图见图6。
3.3.2.5 计算结果
所得结果如下表7所示。
表7采用轴对称单元计算充液膜盒固有频率结果
|
内压—外压(MPa- MPa) |
低压-低压 |
低压-中压 |
低压-高压 |
高压-低压 |
高压-中压 |
高压-高压 |
|
固有频率( Hz) |
22.636 |
22.776 |
22.895 |
24.142 |
24.365 |
24.438 |
3.3.2.6 结果分析
下表8是采用轴对称单元的计算频率与试验的对比。
表 8 充液膜盒固有频率对比
|
膜盒内气压(MPa) |
低压 | ||
|
膜盒外液压(MPa) |
低压 |
中压 |
高压 |
|
试验自振频率(Hz) |
26.25 |
29 |
31.25 |
|
采用轴对称单元的结果(Hz) |
22.636 |
22.776 |
22.895 |
|
相对误差(%) |
13.7 |
21.4 |
26.7 |
|
膜盒内气压(MPa) |
低压 | ||
|
膜盒外液压(MPa) |
低压 |
中压 |
高压 |
|
自振频率(Hz) |
22.25 |
24.5 |
26.75 |
|
采用轴对称单元的结果(Hz) |
24.142 |
24.356 |
24.438 |
|
相对误差(%) |
8.5 |
0.6 |
8.7 |
从结果中可以发现,考虑到流固耦合效应后得到的计算结果从总体上比较接近于试验结果。
4 结论
无论是三维的流固耦合计算还是轴对称流固耦合计算,计算结果相对试验结果来说比较低,这主要是由于试验中膜盒周围密封有一定量的气体,从而导致测得的固有频率要比完全充满水的状态高一些,尤其是在外压不大时(这时外部的流体要相对少些),所以就不可避免地会出现计算的固有频率低一些。
采用轴对称单元进行流固耦合分析的计算结果比较接近试验结果,也说明了流固耦合分析对于膜盒的固有频率计算是极为必要的。
4.1 参考文献
1王心清. 结构设计.宇航出版社,1994。
2 ANSYS手册。
3李东旭.高等结构动力学.国防科技大学出版社,1997.10
4 Bathe, K. J., Finite Element Procedures in Engineering Analysis, Prentice-Hall, Englewood Cliffs ,1982
相关标签搜索:流固耦合的学特性分析 Ansys有限元培训 Ansys workbench培训 ansys视频教程 ansys workbench教程 ansys APDL经典教程 ansys资料下载 ansys技术咨询 ansys基础知识 ansys代做 Fluent、CFX流体分析 HFSS电磁分析 Abaqus培训






