ANSYS剪刃的优化设计

2013-08-12 by:广州ANSYS Workbench软件培训中心来源:仿真在线

ANSYS剪刃的优化设计

优化设计将最优化原理和计算机技术应用于设计领域,为工程设计提供一种重要的科学设计方法。利用这种新的设计方法,设计者可以从众多的设计方案中寻找出最优的设计方案。所谓“最优设计”,指的是一种方案可以满足所有设计要求,而且所需的支出(如重量、面积、体积、应力、费用等)最小,也就是说,最优设计方案就是一个最有效率的方案。在模具优化设计中,对其形状进行优化,是改善应力集中状况、防止裂损、提高寿命和减少材料浪费的主要措施。

1 ANSYS软件的优化原理及方法

    优化设计的基本原理是通过构建优化模型,运用各种优化方法,通过在满足设计要求的条件下迭代计算,求得目标函数的极值,得到最优化设计方案。

    优化问题的数学模型可表示为:

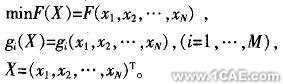
ANSYS剪刃的优化设计ansys培训的效果图片1

    式中,F(X)为设计变量的目标函数,X为设计变量,gi(X)为状态变量。设计变量为自变量,优化结果的取得就是通过改变设计变量的数值来实现的,对于每一个设计变量都有上下限,用户必须规定X中的每一个元素xk(k=1,…,N)的最大值、最小值,它定义了设计变量的变化范围;状态变量是约束设计的数值,是设计变量的函数,状态变量可能会有上下限,也可能只有单方面的限制,即只有上限或只有下限;目标函数是要尽量减小的数值,它必须是设计变量的函数.

    ANSYS优化模块中有2种优化方法:第1种是通用的函数逼近优化方法,其本质是采用最小二乘法逼近,求取一个函数面来拟合解空间,然后再对该函数面求极值。这无疑是一种普遍的优化方法,不易陷入局部极值点,但优化精度一般不高,故多用于粗优化阶段。另外一种优化方法是针对第1种方法的缺陷而改进的方法,叫做梯度寻优。如果说第1种方法是大范围普遍适合的粗优化方法,那么第2种就是局部细化的精优化方法。ANSYS进行优化计算,是一个不断迭代的过程。从理论上讲,任何一种迭代算法都可产生无穷序列的设计方案。在实际优化中,不可能也不必要做无限次迭代,只要达到给定的精度就应该终止计算并认为找到了最优方案。但实际上,对于一个优化问题,其目标函数的理论极小值在哪里预先不可能知道,因此要找到一个理想的终止准则是很困难的,而只能从每一步迭代计算中所得到的信息来进行判断。假设Fj,Xj和Fj-1、Xj-1分别为目标函数、设计变量第j次迭代和第j-1次迭代的结果(Xj为矢量), Fb和Xb分别是当前的最优目标函数和其相应的设计变量值。如果满足或者,为目标函数的公差,那么认为迭代收敛,于是迭代停止。假设或者,那么也认为设计变量的搜索已经趋于收敛,于是迭代停止,也就意味着优化结束。当然,为了防止优化过程在某些问题中不收敛,ANSYS还提供了循环数量控制(注:在0阶函数逼进优化中,默认的最大循环次数为30;默认当连续出现7次不可行解,就认为优化过程发散)。

2 剪刃的优化设计

    2.1问题描述

    本文对精密剪切模具的一个部件—剪刃进行优化设计。剪刃长L=60 mm ,剪刃内半径r=15mm,许用压应力[σ]=225 MPa,材料为高速钢,材料的弹性模量E=210 GPa,泊松比σ=0.3,密度δ=7.8x10,给剪刃内半圆环面加P=13.6865 MPa的压力,剪刃需要优化,以减小重量而能承受最大许用压应力225 MPa为限.可以允许改变剪刃外径大小.

    2.2有限元模型

    进行有限元分析时,假设剪刃在冲剪棒料时,剪刃长度方向的轴向应力为零,问题即可简化为平面应力问题。对剪刃进行建模,在边界处施加位移和力约束,并对模型进行网格划分,剪刃的有限元网格模型.

    2.3优化变量

    模型是在能承受最大压应力225 MPa的工作条件下,追求剪刃的体积最小。根据问题的情况,设剪刃外径为设计变量,用R=30 mm,Pa作为初始设计参数,并建立参数化模型;确定优化设计变量外半径R:Rmin=20 mm,Rmax=50 mm;状态变量为最大等效压应力Smax;目标函数为总体积VTOL.

    综上所述,得本问题的优化设计模型:

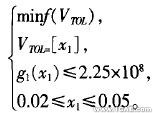
ANSYS剪刃的优化设计ansys分析图片10

    2.4优化设计和分析结果

    按照前文所述原理及方法进行优化设计,得出优化结果(图4、图5、图6)。其中图4、图5显示了剪刃体积VTOL,剪刃外半径R与迭代次数之间的关系,图6为剪刃应力分布图。
    结论:利用上述提出的方法进行优化计算,经过11次迭代,即可收敛于最优解。该外径最小设计方案的最大压应力为Pa,满足不超过Pa的约束要求。该最优设计方案的体积从初始结构的6.3585 mm减小到1.7544 mm,外半径由30 mm减小为20 mm,优化效果十分显著。