基于CAE的试验的结构动力学有限元模型确认
2013-07-24 by:广州ANSYS Workbench软件培训中心 来源:仿真在线
在航空航天工程中,结构动力学有限元建模是气动弹性分析的基础,因此,准确的有限元模型对于气动弹性的分析至关重要。以提高建模精度为目标的有限元模型修正技术的发展日趋完善,并已逐步在航空、航天领域中得到应用,但是模型修正技术未能全面解决建模精度中存在的问题。建模过程中的不确定因素,比如离散化误差、材料物理参数的不确定性、边界条件的近似、缺乏阻尼参数等,将导致有限元模型存在误差。在设计规范中,有限元模型必须通过模态试验或者地面共振试验(GVT)来检验。
最近30多年以来,有限元模型修正技术得到快速发展,根据修正的对象的不同可以分为矩阵型修正和元素型修正。元素型修正是以矩阵元素或结构的设计参数为修正对象。其物理意义明确,相对更具有工程应用价值,而本文则主要采用的基于灵敏度分析的设计参数修正方法。
基于灵敏度分析的设计参数型修正方法主要包括待修正设计参数的选择,灵敏度分析,参数修正以及模型确认等环节。待修正设计参数的选择是模型修正的起始环节,而候选参数是有限元模型存在不确定性因素的参数。在30多年中,发展了很多种参数选择或者误差定位策略与算法,但工程应用中仍然难以准确无遗漏地确定误差参数。
模型确认通过计算与试验两方面的分析,对有限元模型在设计空间的响应预报精度进行评价和确认,并在此基础上进行模型修正,为进一步的应用提供精确可信的有限元模型以及响应计算方法。因此,有限元模型确认的研究目标有两个:结合有限的试验分析,获得精确可信的确定性的有限元模型;并获得进行下一步的响应预报所需要的计算参数,其分析的技术流程如图1所示。
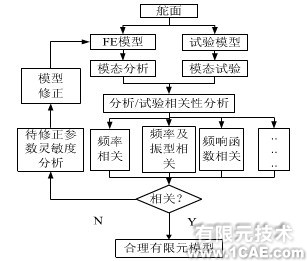
图1 模型确认流程图
本文主要是结合了数值分析技术与试验分析技术,对有限元模型进行修正,然后分析其动力学特性,并将该模型用于后续的颤振分析及结构的动态响应分析中。将有限元法和基于试验数据的模型确认方法结合成分析结构动力学特性的方法,并验证该方法的合理性。通过试验分析数据与修正后的有限元分析数据对比发现,其修正后的有限元精度较高,能够使该模型适合应用于进一步的分析,为分析复杂结构的动力学特性提供参考。
1 研究模型
本文主要是将有限元法、基于试验数据的模型确认技术结合起来,准确地对复杂结构进行动力学建模与分析,而本文主要对简化导弹舵面进行动力学特性的研究,探索并验证该方法的可行性与适用性。
根据实际导弹的气动外形,为了加工制造方便,将该导弹舵面简化为直角梯形,如图2所示,其上底上底a=0.18m,下底b=0.3m,高h=0.23m,厚度t=0.005m,材料为铝,弹性模量E1=70GPa,泊松比μ=0.3,而舵轴材料为刚,弹性模量E2=200GPa,泊松比μ=0.3。
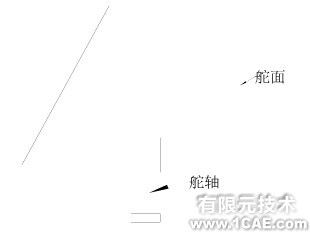
图2 简化舵面模型
2 理论方法
2.1 有限元模态分析
有限元模态分析是利用有限元方法确定结构固有频率和模态的一种计算方法,自由模态分析的整体有限元方程为
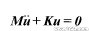
式中M、K分别代表分析模型中的质量矩阵和刚度矩阵,抱歉!图片加载失败。(有限元培训学习,请到1CAE.com学习中心)、u分别代表加速度向量和位移向量。假设结构做简谐振动,则有
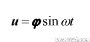
式中φ、ω分别是振型和频率。将式(1)带入式(2)可得到特征值方程为
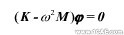
通过求解上述特征值方程,就可以得到结构的固有频率和相对应的模态,基于有限元方法的模态分析方法就是求解结构的固有频率和相对应的模态,通过将连续结构离散化,得到结构整体质量矩阵和刚度阵,利用子空间迭代法、Lanczos法、行列式搜索法等求解结构的特征值。该分析结果对实际工程设计有关参数的选择(比如激振频率、共振现象的避免与利用等)以及进一步的动力响应分析、气动弹性动稳定性分析等都很重要,主要是由于结构的固有特性能够反映结构的动态特性。
2.2 模型确认
2.2.1 相关性理论
为了分析有限元计算的模态或者传递函数与试验测量的模态或者传递函数的一致性,可以通过有限元的数据与试验数据的相关性来进行分析。对于有限元模态与试验模态的相关性,可以表示为如下公式。
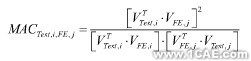
式中VTest,i是第i阶试验模态,VFE,j是第j阶有限元模态,MACTest,i,FE,j是第i阶试验模态VTest,i与第j阶有限元模态VFE,j的相关性值,MACTest,i,FE,j介于0~1之间,由于有限元模态与试验模态不可能完全满足正交性,一般认为有限元模态与试验模态满足的相关性值MAC>0.8,就可以认为有限元模态与试验模态是一致的,如果MAC<0.2,就可以认为有限元模态与试验模态是正交的。
2.2.2 灵敏度分析
灵敏度是对物理参数的变化率,具体为特征值灵敏度δs/δp和特征矢量灵敏度δψ/δp,其中p代表物理参数。特征值的一阶灵敏度一般需要计算质量、刚度阵对设计参变量p的偏导数,在结构动态设计过程中,实际结构简化为杆、梁、板及壳等单元组成的离散结构模型,此时系统的设计变量p一般取杆单元的横截面积;梁单元的横截面积或截面惯性矩;板单元的厚度等。也可以取单元的尺寸和材料常数。
复杂结构的物理参数较多,从结构动力优化设计考虑,必须研究物理参数对其动态特性的灵敏度,这样才能有效地对结构进行动力修正。但是对于整体结构进行物理参数的灵敏度分析有时较为复杂,于是可以只对部件进行灵敏度分析,修正部件的有限元模型,然后利用动态子结构的方法获取整体结构的动力学特性。
2.2.3 基于参数的模型修正
基于参数的模型修正对象主要是表征结构特性的物理参数或几何参数,即设计变量,比如材料弹性模量、密度,杆、梁的横截面积,板、壳的厚度等。一般,修正的目的是使计算与试验测量结果(如固有频率、振型)的误差最小化。
设设计变量为p,结构的质量和刚度阵M(p),K(p)为其函数,其自由振动的广义特征值方程为
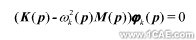
通过求解该特征值方程,可以获得其固有振动的固有频率和模态。而第k阶特征值ω2k(p)(或固有频率) fk(p)=ωk(p)/(2/π)和模态φk(p)亦为p的函数。
设实验测量的固有频率为,假如仅考虑固有频率,则固有频率的计算值fk(p)与实验结果误差(目标函数)定义为
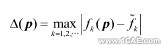
是,基于参数的模型修正可归为非线性规划问题
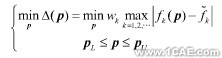
式中pU,pL分别是p的上下限;wk为加权系数。为了方便计算,也可以用平方和代替式(6)中的最大绝对值。一般,式(7)还需要补充强度和刚度条件等约束条件。
对于求解(7)数学规划问题的方法有直接法和间接法等多种方法。其中的直接法包括经典的最速下降法、拟牛顿法、复合形法,以及现在常用的遗传算法、模拟退火法等。而当结构出现重频时,而灵敏度就需要作特殊处理。
3 计算结果与分析
3.1 舵面模态试验
对于该简化导弹舵面模型的模态试验激励方法主要采用力锤法。数据采集方面主要是利用LMS的SCADAS Ⅲ模态分析设备和PCB加速度传感器;测试软件则采用LMS Test.Lab 8B中的Structures Acquisition模块中的Impact Testing,用于锤击法试验模态的采集与分析。
为了获得舵面模态信息,以及通过试验后,对有限元模型进行修正,于是在舵面上布置了14个测点,并在固定夹具位置布置一个参考测点,总共15个测点,如图3所示,分别对4点和14点进行锤击,所以4点和14点的传感器布置在Z轴正向,测量Z向的振动。对于颤振分析,一般只需要舵面的一阶弯曲频率和一阶扭转频率。于是本文中取试验测得的舵面的前2阶固有频率,如表1所示;前2阶模态图如图4所示,其MAC图如图5所示。

图3 舵面模态试验
表1 舵面前2阶固有频率
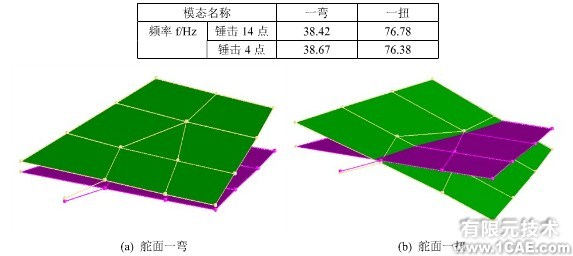
图4 舵面前2阶模态图

图5 试验的MAC图
通过对不同激励点激励所得结果进行对比发现,其固有频率相差很小,但是通过观察LMS软件分析所获得的模态图和频响函数发现,对于锤击14点所得到的结果更接近实际情况,于是选择改组数据作为后续的计算。
3.2 舵面模态试验结果与有限元分析对比
通过对该舵面进行有限元建模,然后进行模态分析,一弯和一扭模态图如图6所示,将所得的分析结果与试验结果进行对比,对比结果如表2所示。如图7所示,是计算有限元与试验的MAC值,前2阶的MAC值都大于0.9,说明有限元建模分析与试验分析的相关性较好,但是由于频率误差较大,需要对有限元模型进行修正。
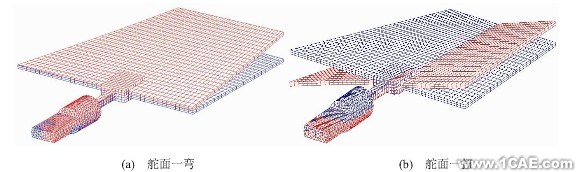
图6 舵面前2阶模态图
表2 舵面前2阶频率对比和MAC值
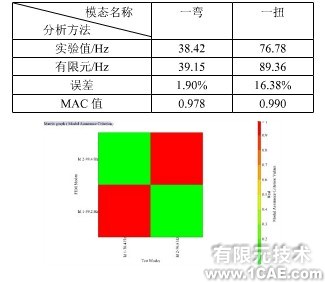
图7 有限元分析与试验分析的MAC值
通过试验分析结果与有限元分析结果对比发现,在第1阶误差相对较小,但是第2阶频率相差较大,这对于颤振分析有很大的影响,于是需要对有限元模型进行修正,然后再利用修正后的模型才能进行下一步分析。
3.3 舵面模型确认
3.3.1 灵敏度计算
由于有限元模型在舵面、舵轴等几何尺寸都与实际试验件一样,于是不需要修改这些几何尺寸,因而不对这些尺寸进行灵敏度分析。由于该舵面结构相对较简单,设计变量相对较少,而且受到试验条件的限制,无法测量试验件的弹性模量,试验件中的螺栓连接在有限元模型中是利用的弹簧单元模拟的。因此本文中主要选择这两个参数对其进行灵敏度分析,即这些参数变化对固有频率的影响。其分析的模态频率对舵轴弹性模量和相关性MAC值对设计变量的灵敏度值如图8所示。
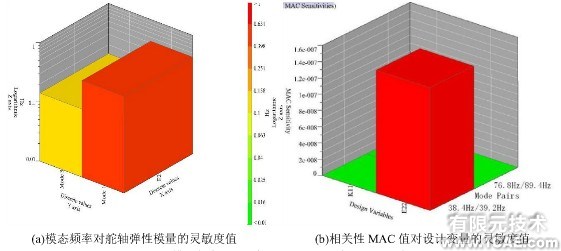
图8 模态频率和相关性MAC对设计变量的灵敏度值
通过灵敏度计算可以发现,在一定范围内,模拟弹簧的刚度值变化主要影响舵面的弯曲频率,而舵轴的弹性模量则影响弯曲频率和扭转频率。于是需要对这两个参数进行修正,使得有限元模型所计算的频率与试验测量的固有频率的误差达到最小值。
3.3.2 舵面模型修正及相关性计算
通过实测试验件的质量与有限元建模所得到的模型质量对比发现,具有一定的偏差,于是首先需要对有限元模型的密度进行修正,使得每个有限元模型部件的质量特性与试验件的一样。并且通过灵敏度分析后,对于本文模型主要是对模拟弹簧单元的刚度值和材料的弹性模量进行参数修正,其参数修正主要利用了MSC.Nastran的优化功能,求解序列为SOL200。主要以模拟弹簧单元的刚度,舵面、舵轴的弹性模量(材料参数) 为设计变量,以频率误差最小为目标函数, 以弯曲频率38.0Hz≤f1≤39.0Hz,扭转频率76.0Hz≤f2≤77.0Hz为约束条件进行优化。其修正结果与试验结果的对比如表3所示,而对修正模型的有限元分析与试验分析进行相关性分析,其分析的MAC值如表3所示,MAC图如图9所示。
表3 修正后舵面前2阶频率对比和MAC值

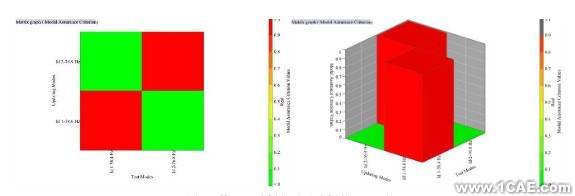
图9 修正后分析与试验分析的MAC值
通过表3所示,其修正后的频率能够达到很高的精度,并且其修正后的MAC值也都大于0.99,说明修正后的模型与试验模型的相关性较好,于是该模型可以用于进一步分析。
4 结论
(1)本文主要介绍了基于试验的结构动力学有限元模型确认方法。对于有限元模型修正涉及的因素比较多,而目前基本没有一种普适算法进行修正。对于不同情况,综合应用各种理论方法、参考多组实测数据,结合工程人员的实际工程经验,才能够获得相对客观、准确的修正模型。
(2)而本文主要利用了试验数据,对有限元模型与试验模型的相关性进行分析,然后对有限元模型进行灵敏度分析,获得需要修正的参数,然后对有限元模型进行修正,通过算例表明该方法能够得到精确度较高的合理模型,能够用于颤振分析以及结构的动态响应分析中。
相关标签搜索:基于CAE的试验的结构动力学有限元模型确认 CAE分析 广州ANSYS培训 Ansys有限元培训 Ansys workbench培训 ansys视频教程 ansys workbench教程 ansys APDL经典教程 ansys资料下载 ansys技术咨询 ansys基础知识 ansys代做 Fluent、CFX流体分析






