建模与网格划分指南第二章

2013-06-19 by:广州有限元分析、培训中心-1CAE.COM 来源:仿真在线

作者: 安世亚太来源: e-works
关键字: CAE 教程网格划分

第二章规划分析方案

2.1规划的重要性

当开始建模时,用户将(有意地或无意地)作许多决定以确定如何来对物理系统进行数值模拟;分析的目标是什么?模型是全部或仅是物理系统的部分?模型将包含多少细节?选用什么样的单元?有限元网格用多大的密度?总之,你将对要回答的问题的计算费用(CPU时间等)及结果的精度进行平衡考虑。你在规划阶段作出的这些决定将大体上控制你分析的成功与否。

2.2确定分析目标

确定分析目标的工作与ANSYS程序的功能无关,完全取决于用户的知识、经验及职业技能,只有用户才能确定自己的分析目标,开始时建立的目标将影响用户生成模型时的其它选择。

2.3选择模型类型(二维、三维等)

有限元模型可分为二维和三维两种。可以由点单元、线单元、面单元或实体单元组成,当然,也可以将不同类型的单元混合使用(注意要保证自由度的相容性)。例如,带筋的薄壳结构可用三维壳单元离散蒙皮,用三维梁单元来离散蒙皮下的筋。对模型的尺寸和单元类型的选择也就决定生成模型的方法。

线模型代表二维和三维梁或管结构,及三维轴对称壳结构的二维模型。实体建模通常不便于生成线模型,而通常由直接生成方法创建。

二维实体模型在薄平板结构(平面应力),等截面的“无限长”结构(平面应变)或轴对称实体结构。尽管许多二维分析模型用直接生成方法并不困难,但通常用实体建模更容易。

三维壳模型用于描述三维空间中的薄壁结构,尽管某些三维壳模型用直接生成方法创建并不困难,但用实体建模方法通常会更容易。

三维实体分析模型用于描述三维空间中截面积不等,也不是轴对称的厚结构。用直接生成的方法建立三维实体模型较复杂,实体建模会使其变得容易些。

2.4线性和高次单元的选择

ANSYS程序的单元库包括两种基本类型的面和体单元:线性单元(有或无特殊形状的)和二次单元。这些基本单元类型如图2-1所示,下面来探讨这两种基本类型单元的选择。

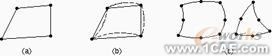
建模与网格划分指南第二章ansys结构分析图片1

图2-1面和体类型。

(a)线性等参元

(b)特殊形状的线性等参元

(c)二次单元

2.4.1线性单元(无中间节点)

对结构分析,带有附加形函数的角点单元会在合理的计算时间内得到准确的结果。当使用这些单元时,要注意防止在关键区域的退化形式。即避免在结果梯度很大或其它关注的区域使用二维三角形单元和楔形或四面体形的三维线单元。还应避免使用过于扭曲的线性单元,对于非线性结构分析,如果使用线性单元细致地而不是用二次单元相对粗糙的进行网格划分,那么将以很少的花费获得很好的精度。

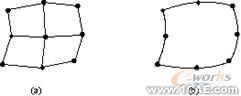
建模与网格划分指南第二章ansys结构分析图片2

图2─2 网格的比较

(a)线性单元和(b)二次单元的例子如图2-2。

当对弯曲壳体建模时,必须选用弯曲的(二次的)或平面(线性)的壳单元,每种选择都有其优缺点,对于多数的实际情况,主要问题利用平面单元以很少的计算时间,即可获得很高精度的结果。但是,必须保证使用足够多的平面单元来创建曲面。明显地,单元越小,准确性越好。推荐三维平面壳单元延伸不要超过15度的弧,圆锥壳(轴对称线)单元应限制在10度的弧以内(或离Y轴5度)。

对多数非结构分析(热、电磁等),线性单元几乎与高次单元有同样好的结果,而且求解费用较低。退化单元(三角形和四面体)通常在非结构分析中产生准确结果。

2.4.2 二次单元(带中间节点)

对于用退化的单元形式进行的结构分析(即二维三角形单元和楔形或三维四面体单元),二次单元通常会以比线性单元的求解费用更低且产生良好的结果。可是,为正确地使用这些单元,需要注意它们的特殊的性质:

· 对于分布载荷和面压力不象线性单元按一般意义上分配到单元节点上(见图2-3),单元的中间节点对反力也表现出相同的非直观的解释。

· 三维带中间节点的热流单元在承受对流载荷时按固定模式分配热流,在中间节点沿一个方向流动而在角点又沿另外方向的流动。

· 对于结构单元,中点节点的温度如果在两相邻角点温度范围之外则要重新定义为这两角点的平均温度。

· 由于中间节点的质量也大于角节点的质点,所以通常将中间节点选为主自由度(对于减缩自由度分析)。

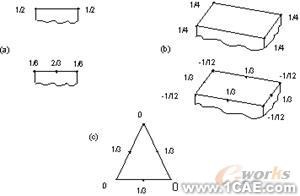
建模与网格划分指南第二章ansys结构分析图片3

图2─3 节点分配的平衡

(a)二维单元

(b)三维单元

(c)三维三角形单元

· 由于质量分配不均匀,在动力分析中感兴趣的波传波技术不推荐使用带中间节点的单元。

· 不要在有中间节点(CONTAC12, COMBIN40, CONTAC48, CONTAC49, and CONTAC52)的边定义节点为基础的接触单元,也不要将间隙单元与带中间节点的边连接。类似地,对热问题,不要应用辐射连接或非线性对流表面到带有中间节点的边。节点为基础的接触要同有中间节点的表面接触,中间节点应该去掉。对面对面接触单元不用担心(TARGE169, TARGE170, CONTA171, CONTA172, CONTA173, and CONTA174)。划分实体模型时提供了一些方法忽略一些中间节点。

· 当约束一个单元(或表面)的边缘自由度,包括中间节点在内的边缘上所有的节点都要约束。

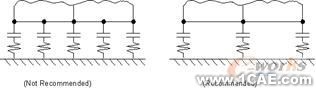
建模与网格划分指南第二章ansys结构分析图片5

图2—4 在间隙或接触表面处避免中间节点

· 单元的角点只能与单元的角点相连,而不能与相邻单元的中间节点相连。相邻的单元应该有相连(或共同的)中间节点

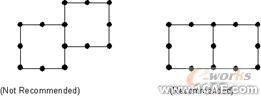
建模与网格划分指南第二章ansys结构分析图片6

图2─5 避免单元间中间节点与角点相连

· 对于有中间节点的单元,通常希望每一个这样的中间节点在相应角点之间连线的中点位置,可是,有时却希望出现在其它地方:

─节点沿着弯曲的几何边界通常可产生更准确的分析结果─所有的ANSYS网格划分器缺省地将它们放在那里。

─有的内边界也不得不弯曲以防止单元倒置或过于扭曲,ANSYS网格划分器有时也产生这种弯曲。

─用带有故意将中间节点偏离中心四分之一点可以模拟裂纹尖端的奇异性,利用ANSYS的KSCON命令可以产生这种特殊的面网格。(Main Menu>Preprocessor>-Meshing-Size Cntrls>-Concentrat KPs-Create)

· 中间节点位置可由下面描述的单元形状测试进行检查(对于控制单元形状的检查信息可参见本手册的§7章)。

──除三节点三角形和四节点四面体外的所有实体和壳单元都要进行实三维空间与单元本身的自然坐标空间一致性映射的测试。雅可比比值过大表明单元过于扭曲,可能是由中间节点的位置设置不当引起的。关于雅可比比值测试的细节,参见《ANSYS, Inc. Theory Reference》中的单元形状测试部分。

· 如果不给中间节点指定位置,程序会自动按线性笛卡尔坐标插值将中间节点放在两角点的中间,按此法放置的节点的节点坐标系旋转角度也是按线性插值得到。

· 在相连单元的公共边应有相同的节点数,当混合单元类型时有必要从一个单元去除中间节点。例如,图2-6中的8节点单元与一个4节点单元相连时应把8节点单元的N节点去掉(或在生成这个单元时给它一个0节点号)。

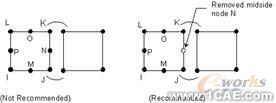
建模与网格划分指南第二章ansys结构分析图片7

图2─6 避免单元相交时中点节点不匹

注意: 程序在下列情况会自动地将线性和二次单元共同一侧的中间节点去掉:一个面(或体)用线性单元划分网格〔AMESH、VMESH、FVMESH〕,然后相邻面(或体)用二次单元划分网格。如果网格划分的次序颠倒了,中间点节则不能去掉(先分二次单元,后分线性单元)。

· 去掉了中间节点意味着边缘仍保持直的,相应地导致刚度增加,建议只在过渡区域使用去掉中间节点的单元,而不在增加了形函数的简化线单元处使用。如果需要,那么在产生单元之后可利用下列命令增加或去掉中间节点:

命令:EMID

GUI : Main Menu>Preprocessor>Move / Modify>Add Mid Nodes

Main Menu>Preprocessor>Move / Modify>Remove Mid Nd

命令:EMODIF

GUI : Main Menu>Preprocessor>Move / Modify>Modify Nodes

· 二次单元并不比线性单元的积分点多。因此,在非线性分析中优先使用线性单元。

· 诸如平面PLANE82和SHELL93的高阶四边形单元的一种网格可由于零变形能而产生奇异。

· 对后处程序只用截面的角点和隐藏线显示,类似地,节点应力结果的输出和后处理只能对角节点进行。

· 在图形显示时,曲边形的中间节点单元显示为直线段(除非使用Powergaphics)模型因此看起来比实际的要粗糙些。

2.5不同单元连接的限制

在连接有不同自由度(DOFs)的单元时必须小心,因为在界面处可能会发生不协调的情况,当单元彼此不协调时,求解时会在不同单元之间传递不适当的力或力矩。

为保证协调,两个单元必须有相同的自由度。例如,它们必须有相同数目和类型的位移自由度及相同数目和类型的旋转自由度,而且,自由度必须是耦合的,即它们必须连续地穿过界面处单元的边界。

考查三个应用了不协调单元的例子:

· 单元有不同个数的自由度是不协调的,SHELL63和BEAM4单元每个节点有三个平动和三个转动自由度。Solid45 单元每个节点有三个平动自由度,但缺少转动自由度。如果Solid45单元与SHELL63或BEAM4单元相连,相应平动自由度的节点力会传到实体块单元上。但是,相应SHELL63和BEAM4单元的转动自由度的节点位移则不会传递给SOLID45单元。

· 单元有相同个数的自由度也不总是协调的。BEAM3(二维弹性梁)单元和SHELL41(薄膜壳)单元每个节点都各有三个自由度。可是,壳单元有三个平动自由度(UX、UY和UZ),而梁单元只有两个平动自由度(UX和UY),因为只有UZ的结果能反映壳单元的刚度,而且壳单元没有转动自由度(ROTZ)而梁单元有。与梁单元旋转自由度对应的节点位移将不会传递给壳单元,界面表现为梁象是被钉住了。

· 三维梁单元与三维壳单元每个节点都有6个自由度,可是,壳单元的ROTZ自由度是与平面内旋转刚度相联系的,这是一个虚构的刚度;即它不是数学计算的真实刚度,因此壳的ROTZ自由度不是真实的自由度。(例外是当SHELL43或SHELL63单元(两者都有KEYOPT(3)=2)的Allman旋转刚度被激活时),因此对三维梁单元仅有一个节点与三维壳单元相连导致梁单元的旋转自由度与壳单元的ROTZ自由度对应是不协调的,不应该将梁单元与壳单元按此方式连接起来。

类似的不协调也可在不同数目和(或)类型自由度的单元之间存在。

这些问题并不会使分析无效,但至少应该注意到两个不同类型单元交界的条件。

2.6 找到利用对称性的办法

许多物体都有某种对称,重复对称(如一个长管道上平均分布的散热片,反对称(如塑料容器的模子),或轴对称(如灯炮)。当一个物体在所有方面都是对称的(几何、载荷、约束和材料属性),可以利用用述事实减少模型的大小和范围。

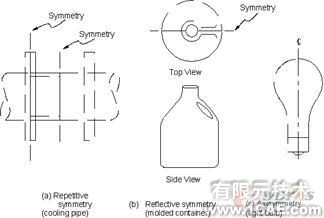
建模与网格划分指南第二章ansys结构分析图片8

图2-7对称的例子

(A)重复对称(散热等)(B)镜像对称(模铸容器)(C)轴对称(灯炮)

2.6.1轴对称结构的说明

任何表现在为对一中心轴几何对称的结构(如旋转壳或实体)是轴对称。例如直管、圆锥、圆盘、圆盖等。

三维轴对称结构的模型可用二维形式等效。可以想象得到二维轴对称分析较相应的三维分析更精确。

由定义可知,一个完全轴对称模型只能施加轴对称载荷。但在很多情况下,轴对称结构实际受的并不是轴对称载荷,必须利用一种特殊的轴对称谐波单元,来建立轴对称结构二维模型的非轴对称载荷。详见《ANSYS Elements Reference 》中的§2.10一节。

2.6.1.1对轴对称结构的一些特殊要求

对轴对称结构模型的特殊要求有:

· 对称轴必须与总体笛卡尔坐标的Y轴重合。

· 不允许出现负的X方向节点坐标。

· 总体笛卡尔坐标Y方向代表轴向,总体笛卡尔坐标X方向代表径向,总体笛卡尔坐标Z方向代表周向。

· 模型应当用适当的单元类型组合在一起:

——对轴对称模型,可用二维实体且KEYOPT(3)=1,和(或)轴对称壳体。而且,可用不同的连接,接触,组合及表面单元并可将轴对称实体和壳单元容在一个模型里。(除非是轴对称实体或壳单元否则程序不会识别其它的单元)如果《ANSYS Elements Reference 》没有对一个特殊单元类型讨论其在轴对称结构中的应用,那么不要使用此种单元类型进行轴对称分析。

——对轴对称谐波模型,只能使用轴对称谐波单元。

· SHELL51和SHELL61单元不应位于总体Y轴上。

· 对包含二维实体单元的模型剪切影响是重要的,在厚度方向上至少要使用二个单元。

2.6.1.2进一步的须知和限制。

如果结构沿对称轴包含有孔,不要忘记在Y轴和二维轴对称模型间留适当的距离(见图X方向的偏移表示一个轴对称孔。)对轴对称载荷的讨论参见《ANSYS Basic Analysis Guide》的§2。

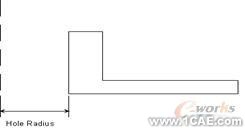
建模与网格划分指南第二章ansys结构分析图片9

图2-8X方向的偏移表示一个轴对称孔

2.7决定包含多少细节

一些小的细节对分析来说不重要,不必在模型中体现,因为它只会使你的模型过于复杂。可是对有些结构,小的细节如倒角或孔可能是最大应力位置之所在,可能非常重要,取决于用户的分析目的。必须对结构的预期行为有足够的理解以对模型应包含多少细节做出适当的决定。

有些情况下,仅有一点微不足道的细节破坏了结构的对称。那么,可以忽略这些细节(或相反的将它们视为对称的),以利于用更小的对称模型,必须权衡模型简化带来的好处与精度降低的代价来确定是否对一个非(拟)对称结构故意忽略其非对称细节。

2.8确定合适的网格密度

有限元分析中经常碰到的问题是单元网格应划分得如何细致才能获得合理的好结果?不幸的是,还没有人能给出确定的答案;你必须自己解决这个问题,关于这个问题的解决可求助于以下一些技术:

· 利用自适应网格划分产生可满足能量误差估计准则的网格(此技术只适用于线性结构静力或稳态热问题,对什么样的误差水平是可接受的判断依据于你的分析要求)。自适应网格划分需要实体建模。

· 与先前独立得出的实验分析结果或已知解析解进行对比。对已知和算得结果偏差过大的地方进行网格细化。(对所有的由四面体组成的面或体网格可用NREFINE、EREFINE、KREFINE、LREFINE和AREFINE命令(Main Menu> Proprocessor>-Meshing-Modify Mesh>-Refine At-entity type)进行局部网格细化)

· 执行一个你认为是合理的网格划分的初始分析,再在危险区域利用两倍多的网格重新分析并比较两者的结果。如果这两者给出的结果几乎相同,则网格是足够的。如果产生了显著不同的结果,应该继续细化你网格直到随后的划分获得了近似相等的结果。

· 如果细化网格测试显示只有模型的一部分需要更细的网格,可以对模型使用子模型以放大危险区域。

网格划分密度很重要,如果网格过于粗糙,那么结果可能包含严重的错误,如果网格过于细致,将花费过多的计算时间,浪费计算机资源,而且模型可能过大以致于不能在你的计算机系统上运行,为避免这类问题的出现,在生成模型前应当考虑网格密度问题。

开放分享：优质有限元技术文章,助你自学成才