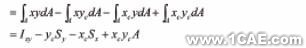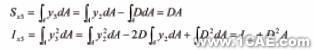AutoCAD计算截面对任意轴的静距和惯性矩的程序设计
2013-08-09 by:广州cad教学中心 来源:仿真在线
AutoCAD计算截面对任意轴的静距和惯性矩的程序设计
一、引言
Autodesk公司开发的AutoCAD工程绘图软件是当前应用广泛的二维CAD软件,功能强大,在机械设计领域广泛应用。开放式体系结构也允许第三方开发者为它编写应用程序,显著增加了绘图工作效率。
VBA是VisualBasicforApplications的英文缩写,是由Microsoft公司创建的,它是一个功能强大的定制程序开发工具,用来自动执行任务的一个编程环境。VBA为AutoCAD的二次开发提供类似VisualBasic(VB)语言所拥有的功能,引入了对象的程序设计环境,为开发者提供了用来创建图形用户界面(GUI)的可拖拉工具和用来与AutoCAD对象交互的编程语言。
AutoCAD具有强大的绘图功能,可以直接求得截面对当前坐标系x轴和y轴的惯性距,但不能求得对任意轴的静距和惯性矩。需要用户通过创建面域、变换坐标系等一系列操作进行求解。静距和惯性矩分别是计算回转体质量、校核受力零部件强度的重要的截面几何性质。笔者使用VBA在AutoCAD平台上进行二次开发,根据静距和惯性距的平行移轴公式和转轴公式定制应用程序,帮助工程设计人员自动高效率地完成截面对任意轴的静距和惯性矩求解。
二、数学模型求解
根据平面图形的平行移轴公式、转轴公式,可推导出平面图形对于任意轴的静距和惯性矩。已知截面在XOY坐标系下的面积A、质心(xc,yc)、惯性距Ix、惯性距Iy和惯性距Ixy,求解截面对X3轴的静距Sx3、惯性距Ix3。
步骤1:截面对x、y轴的静距:Sx=ycA,Sy=xcA;
步骤2:通过平行移轴到形心(xc,yc)后,截面中任意一点在X1O1Y1坐标系下的坐标为:
x1=x-xc
y1=y-yc
求解对x1、y1轴的静距、惯性距和惯性积。
因为形心在X1O1Y1坐标系的原点,所以Sx1=0,Sy1=0。
步骤3:围绕形心(xc,yc)逆时针旋转θ,图形中任意一点在X2O2Y2坐标系下的坐标为:
x2=x1cosθ+y1sinθ
y2=-x1sinθ+y1cosθ
求解对x2、y2轴的静距、惯性距和惯性积。因为形心在X202Y2坐标系的原点,所以Sx2=0,Sy2=0。
步骤4:通过沿y3方向平行移轴到x3轴后,图形中任意一点在X3O3Y3坐标系下的坐标为:
x3=x2
y3=y2-D
求解对x3轴的静距、惯性距:
通过平行移轴和转轴很容易求解平面图形对于任意轴的几何性质,推导过程中所需要的已知数据,可以采用VBA程序在AutoCAD的模型空间获得。
三、VBA设计思路
本文通过为指定区域创建面域Region对象,可以获得Region对象的Area、Centroid、MomentOfInertia和ProductOfInertia属性。在VBA中通过程序代码实现数学模型求解过程,从而实现截面对任意轴的静距和惯性矩求解。
四、VBA程序编写
1.生成面域
首先介绍生成面域并处理的方法,在AutoCAD模型空间中所求区域指定一点,为所选区域生成面域,并使此面域处于绘图顺序的最顶层。此面域为模型空间中最新的实体对象,因此可以根据模型空间的实体数量,将此面域赋值给AcadRegion类型变量RegionTemp,再将Region和RegionTemp指定的两个面域合并,其次变更Region的颜色以便突出显示对象。此过程采用循环语句让用户可以选取多个区域并生成一个Region。为了便于调用代码,创建自定义函数如下:
FunctionAddRegion(ByRefRegionAsAcadRegion,ColorAsACAD_COLOR)
DimP0AsVariant
DimRegionTempAsAcadRegion
DimOSIntAsInteger
on ErrorResumeNext
OSInt=ThisDrawing.GetVariable(“OSMODE”)
‘获取对象捕捉数值
ThisDrawing.SendCommand“OSMODE31743“
‘取消对象捕捉loopstart:DoWhile1
P0=ThisDrawing.Utility.GetPoint(,vbCrLf&“请在轮廓线内点取一点:”)
IfErr<>0Then
Err.Clear
GoToErrorHandler
EndIf
PStr=P0(0)&“,”&P0(1)
lngnum=ThisDrawing.ModelSpace.Count
‘创建面域
ThisDrawing.SendCommand“-boundaryAORin
“&““&““&PStr&““&““
Iflngnum=ThisDrawing.ModelSpace.CountThen
GoToloopstart
EndIf
IfThisDrawing.ModelSpace.Item(lngnum).EntityName
=“AcDbRegion”Then
SetRegionTemp=ThisDrawing.ModelSpace.Item(lngnum)
EndIf
‘面域求和
Region.BooleanacUnion,RegionTemp
IfErr<>0Then
Err.Clear
SetRegion=RegionTemp
54www.idnovo.com.cn
栏目主持:黎艳
投稿信箱:liy@idnovo.com.cn
EndIf
Region.Color=ColorRegion.UpdateRegion.HighlightTrueLoop
ErrorHandler:
ThisDrawing.SendCommand“OSMODE“&OSInt&““‘回复对象捕捉EndFunction
2.获得面域属性
面域生成之后,我们可以获得面域对象的属性,从而得到面域对x、y轴的几何性质。具体的自定义函数代码如下:
FunctionGetRegionAtt(ByRefRegionobjAs
AcadRegion,_
ByRefA,ByRefCx,ByRefCy,_
ByRefSx,ByRefSy,ByRefIx,ByRefIy,ByRefIxy)on ErrorResumeNext
A=Regionobj.Area’面积
Cx=Regionobj.Centroid(0)’质心Cy=Regionobj.Centroid(1)
Sx=Cy*A’计算静距Sy=Cx*A
Ix=Regionobj.MomentOfInertia(0)’惯性距Iy=Regionobj.MomentOfInertia(1)
Ixy=Regionobj.ProductOfInertia’惯性积EndFunction
3.程序求解
根据数学模型求解中的公式,我们可以采用VBA编写代码求解。公式推导时所用到的参数任意轴对x轴的角度θ、面域质心到任意轴的距离D,需要通过VBA程序求解。在AutoCAD中可以使用“ThisDrawing.Utility.AngleFromXAxis”方法获得指定两点所形成的直线对x轴的弧度值。在VBA中计算三角函数时采用的参数为弧度,所以编写代码时可以直接用Radian变量代替角度θ。具体按公式求解的自定义函数代码如下:
FunctionCalculate(ByRefRegionobjAsAcadRegion,ByRefA,ByRefCx,ByRefCy,_
ByRefSx,ByRefSy,ByRefIx,ByRefIy,ByRefIxy,_ByRefSx1,ByRefSy1,ByRefIx1,ByRefIy1,ByRef
Ix1y1,_
ByRefSx2,ByRefSy2,ByRefIx2,ByRefIy2,ByRef
Ix2y2,_
ByRefSx3,ByRefSy3,ByRefIx3,ByRefIy3,ByRef
Ix3y3)
on ErrorResumeNext
‘指定惯性轴两点
P1=ThisDrawing.Utility.GetPoint(,vbCrLf&“请选取惯性轴第一点:”)
P2=ThisDrawing.Utility.GetPoint(P1,vbCrLf&“请选取惯性第二点:”)
Radian1=ThisDrawing.Utility.AngleFromXAxis(P1,P2)
IfStr(P1(0))=Str(Cx)AndStr(P1(1))=Str(Cy)Then
Radian2=0
Else
Radian2=ThisDrawing.Utility.AngleFromXAxis(P1,CP)
EndIf
DimCP(0To2)AsDouble
CP(0)=Cx
CP(1)=Cy
DisPP=Sqr((Cx-P1(0))^2+(Cy-P1(1))^2)‘质心到P1点的距离
Radian=Radian2-Radian1惯性轴对于x轴弧度
DisPL=Abs(DisPP*Sin(Radian))‘质心到惯性轴的距离
‘移轴至质心
Sx1=Sx-Cy*ASy1=Sy-Cx*A
Ix1=Ix-2*Cy*Sx+Cy^2*AIy1=Iy-2*Cx*Sy+Cx^2*A
Ix1y1=Ixy-Cy*Sy-Cx*Sx+Cx*Cy*A‘转轴
Sx2=Sx1*Cos(Radian1)-Sy1*Sin(Radian1)Sy2=Sy1*Cos(Radian1)+Sx1*Sin(Radian1)
Ix2=Ix1*Cos(Radian1)^2+Iy1*Sin(Radian1)^2-
2*Ix1y1*Sin(Radian1)*Cos(Radian1)
Iy2=Iy1*Cos(Radian1)^2+Ix1*Sin(Radian1)^2+
2*Ix1y1*Sin(Radian1)*Cos(Radian1)
Ix2y2=0.5*(Ix1-Iy1)*Sin(2*Radian1)+Ix1y1*Cos(2*Radian1)‘二次平行移轴
Sx3=Sx2+DisPL*A’所求静距
Ix3=Ix2+DisPL^2*A’所求惯性矩EndFunction
相关标签搜索:AutoCAD计算截面对任意轴的静距和惯性矩的程序设计 AutoCAD计算截面对任意轴的静距和惯性矩的程序设计 AutoCAD培训 AutoCAD培训课程 AutoCAD图纸设计 AutoCAD在线视频 AutoCAD技术学习教程 AutoCAD软件教程 AutoCAD资料下载 Fluent、CFX流体分析 HFSS电磁分析 Ansys培训 Abaqus培训