ANSYS与LS-DYNA联合解决薄壁钢管在轴向冲击下的屈曲
2013-06-07 by:广州有限元分析、培训中心-1CAE.COM 来源:仿真在线
本文以薄壁钢管在轴向冲击作用下的屈曲分析为例,介绍在ANSYS/LS-DYNA中进行冲击动力学分析的方法。ANSYS/LS-DYNA将显式计算程序LS-DYNA 与ANSYS仿真分析环境有机的结合在一起,可以完成高度非线性的瞬态动力过程的分析。两者的结合既克服了ANSYS在瞬态动力过程分析方面的弱点,同时也克服了LS-DYNA在建模方面的不方便性,两者的合并,无疑克服了各自的缺点,同时将两者的优点保留了下来。
作者: 倪欣 来源: e-works
关键字: ansys ls-dyna 薄壁钢管 屈曲
1 前言
冲击作用是在建筑桩基施工、金属加工和动力机械设计等问题中常见的现象,结构在冲击载荷下的材料强度以及动力响应问题(主要是变形和屈曲问题)一直是一项很重要的动力学研究课题。各种冲击动力学问题的最基本特征为冲击物的速度或位移在与结构接触后的一个极短时间内迅速地改变,冲击作用的(加载)过程非常短暂。
本文以薄壁钢管在轴向冲击作用下的屈曲分析为例,介绍在ANSYS/LS-DYNA中进行冲击动力学分析的方法。ANSYS/LS-DYNA将显式计算程序LS-DYNA 与ANSYS仿真分析环境有机的结合在一起,可以完成高度非线性的瞬态动力过程的分析。两者的结合既克服了ANSYS在瞬态动力过程分析方面的弱点,同时也克服了LS-DYNA在建模方面的不方便性,两者的合并,无疑克服了各自的缺点,同时将两者的优点保留了下来。
2 模型建立与数值讨论
实际生活中经常使用薄壁钢管支撑重物用,但是经常会发生这样的问题:但重物的重量慢慢增加时,薄壁钢管突然会发生弯曲。这就是所谓的屈曲。一旦结构发生了屈曲,结构已经丧失了稳定性,轻则不能承载重物,重则会危机生命。用理论可以分析简单的结构屈曲,但是实际生活中的结构太复杂,以至于不能简单的运用理论进行分析了,必须借助CAE软件了,因此本文有很大的实用价值。
要分析的问题描述如下:圆钢管直径为D=500mm,壁厚t=3mm,长度L=1000mm,一端完全固定,另一端按强制性位移进行加载,使端面在20ms内沿轴向发生500mm的压缩位移,分析钢管在整个过程中的变形以及应力分布情况,最后进行一些讨论。
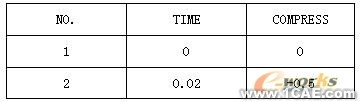
在分析中采用SHELL163显式分析单元,单元变形方法选用Belytschko-Wong方法,这种单元算法比较适合于处理有表面翘曲的大变形问题。材料的密度为7800kg/m3,泊松比为0.27,弹性模量为2.07e11,屈服应力为300MPa,切线模量为1e10。由于钢管表面在冲击压缩过程中,可能会发生表面折叠和自相接触的现象,因此需要定义接触,接触算法采用单面的自动接触算法ASSC,接触面的摩擦系数取为0.1。冲击载荷定义如下:
表1 载荷-时间数组取值
用ANSYS进行建模,网格好后的模型如图1。

图1
下面动态显示结构的变形情况,如图2。从图中可以清楚地看到,一开始变形主要集中在薄壁钢管的顶部和底部,从图3中可以进一步看到一开始变形发生在钢管的底部,即固定端,随即变形区域逐渐扩大,慢慢的扩大到顶部。随着时间推移,底部和顶部的变形越来越大,但是钢管中部部分基本上没有发生变形。在卸去冲击载荷后,即20ms后,薄壁钢管开始恢复原来的状态,图2中的右下图显示了20.7ms时的钢管的变形情况,可见圆形钢管不可能变到原来的状态,可见在此冲击载荷下,薄壁钢管已经发生塑性变形,故不可能恢复到未加载时的形状了,相应的情形也可以在后面的图片中看到。

图2
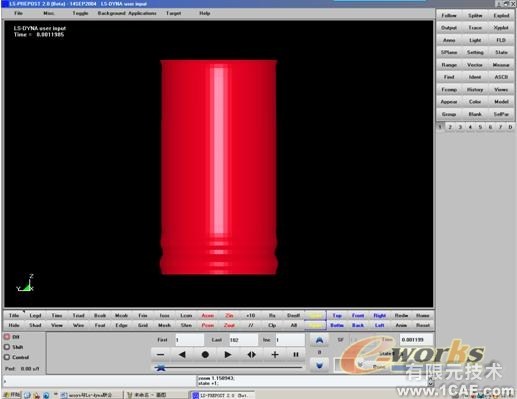
图3
下面动态显示结构的Von Mises应力分布情况,如图4。图中显示了不同时刻钢管的应力分布情况。从图中可以看出,随着位移载荷的逐渐增大,钢管中的最大应力也急剧增大,可以看出在这样的位移载荷下,材料早已经承受不住了,最大应力已经远远超过了材料的屈服应力,材料将被完全破坏。还可以看出,在卸载后,钢管恢复过程中的最大应力居然大大超过了加载过程中的最大应力,所以在卸载后结构更加危险。
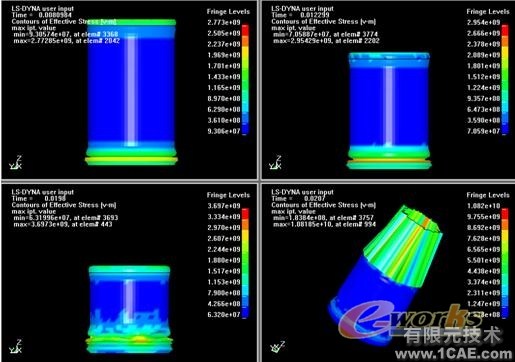
图4
图5中动态显示了钢管的塑性应变的分布情况。从图中可以看出,系统在加载过程中,顶面和底面将出现幅值很大的塑性应变,而在中间部位,塑性应变很小,接近于0。在卸载后,塑性应变将进一步增大,最大值将发生在钢管的顶面,所以如果要对钢管的变形进行控制的话,中间部位可以不用管它,主要解决钢管顶面和底面的结构即可控制整个模型的变形。
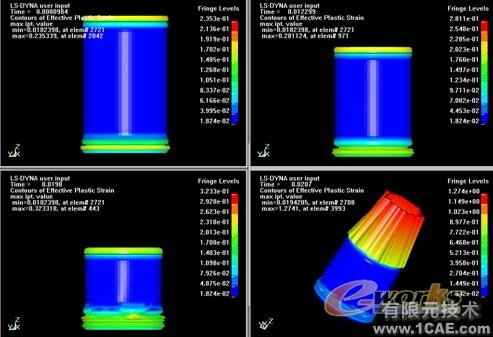
图5
3 结论
最后,结合本例,谈谈在分析冲击动力学方面的问题应该注意的事项。
(1)注意采用正确的材料分析模型。
(2)对于薄壳单元,注意在计算中应该采用沙漏控制。
(3)在大变形问题中(冲击动力学主要研究这类问题),可以采用壳单元的自适应网格划分技术。
(4)在冲击作用区域,如需对真实的局部应力分布情况进行模拟,则需要划分相当细密的单元网格,在非冲击区域,单元网格可以适当进行放大,而对整个模型不会产生很大的影响。
(5)沿壳单元厚度方向,应采用多个积分点,以得到薄壳厚度方向的应力分布情况。
(6)对于可能发生接触的界面之间,需定义正确的接触算法类型以反映实际情况;对于人工判断可能有困难的地方,建议采用自动接触算法,程序在计算时将自动进行接触判断,这一算法可以用于任何复杂的接触行为和过程。
(7)在建模过程中,冲击物材料可采用刚性体,可以加快计算过程,刚性体即使采用很密的单元网格也不是增加计算机的计算时间的。
相关标签搜索:ANSYS与LS-DYNA联合解决薄壁钢管在轴向冲击下的屈曲 Fluent、CFX流体分析 HFSS电磁分析 Ansys培训 Abaqus培训 Autoform培训 有限元培训 Solidworks培训 UG模具培训 PROE培训 运动仿真






